В статье приводятся результаты изучения напряженно-деформированного состояния породного массива месторождения Акбакай и Акжал Республики Казахстан. Установлена зависимость горизонтальных напряжений от глубины залегания горных пород, позволяющая прогнозировать напряженно-деформированное состояние массива.
Ключевые слова: горные породы, напряженное состояние массива, глубина горных работ, зависимость, анализ точности.
The article presents the results of studying the stress-strain state of the rock massif of the Akbakai and Akzhal deposits of the Republic of Kazakhstan. The dependence of horizontal stresses on the depth of bedding of rocks has been established, which makes it possible to predict the stress-strain state of the massif.
Keywords: rocks, stress state of the massif, depth of mining, dependence, accuracy analysis.
Важнейшей геомеханической характеристикой массива горных пород является его естественное напряженное состояние. Этому вопросу уделяется большое внимание, особенно за последние 20–25 лет.
Более 100 лет назад известный швейцарский геолог А.Гейм [1], выдвинул гипотезу, согласно которой напряженное состояние земной коры в любой ее точке является функцией глубины залегания горных пород. Гейм полагал, что напряжения в земной коре должны распределяться по гидростатистическому закону, т. е.
х=у=z=Н, (1)
где х, у — нормальные горизонтальные напряжения;
z — нормальное вертикальное напряжение;
-объемный вес породы;
Н — глубина дневной поверхности.
В двадцатых годах прошедшего столетия А. Н. Динник [2], в качестве модели массива горных пород в связи с задачей расчета крепи выработок принял упругую однородную изотропную гравитирующую среду с жестко ограниченными горизонтальными перемещениями. Согласно А. Н. Диннику,
z=Н,(2)
х=у=Кz,(3)
где К=
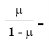

Обе эти модели напряженного состояния массивов скальных пород были выдвинуты, исходя из допущений о геомеханической однородности и изотропности массивов, и, по существу, модель Гейма можно получить из модели Динника, если принять коэффициент бокового распора породы равным 1,0. Последнее условие выполняется, когда значение коэффициента Пуассона горной породы
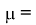
Анализируя литературу, посвященную проблемам механики скальных пород, не трудно заметить, что во многих случаях наблюдается определенная разобщенность между представлениями о геомеханической структуре реального породного массива и о его наряженном состоянии. Очевидно, для определенного круга задач, когда масштабы факторов неоднородности существенно меньше масштабов изучаемого массива конкретного месторождения или масштабов горных выработок, взаимодействующих с элементами этого массива, можно принять модель сплошного однородного тела. Поэтому рассматриваемый нами массив горных пород детально исследован экспериментальными методами, но полученные результаты являются составной частью исследований по изучению геомеханических процессов и следует рассматривать их не как окончательные, а итог определенного этапа работ.
Методы и средства изучения. Кнастоящему времени выработаны различные методы и способы контроля за состоянием породного массива. К числу основных можно отнести: метод разгрузки ВНИМИ [3], дискования керна [4], ультразвуковой [5] и др. Для изучения напряженного состояния массивов пород месторождения Каратау (1995–2000гг) и Акбакайского месторождения (20125–2015гг) нами был изучен керновый материал геологоразведочных скважин [3,4] и метод дискования. При проведении геотехнологических исследований устойчивости горных пород с выдачей рекомендации по управлению горным давлением на руднике Акжал ТОО «Nova Цинк» -был использован комплект аппаратуры ВНИМИ и разработанный нами способ определения нарушенности массива [6].
В расчетные формулы для вычисления напряжений по результатам измеренных деформаций входят модуль упругости и коэффициент Пуассона. Величины модуля упругости
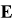
Общий порядок определения напряжений методом заключается в следующем. B исследуемом участке массива задаются две или три скважины. Направление скважин ориентируется по направлениям главных напряжений в массиве. Эти направления определяются предварительным изучением геомеханической ситуации на месторождении путем привлечения тектонических методов и визуальной оценки характера и условий разрушения и деформирования пород вокруг выработок. Целесообразно начинать измерительные работы от вертикальной скважины, ориентированной вдоль главного нормального напряжения z(З). Результаты обработки полученных данных позволят уточнить направление главных горизонтальных напряжений: х (1) и у(2).
Важным моментом при определении напряжений по результатам измерений деформаций при торцевом варианте метода разгрузки является способ перехода от измеренных деформаций к напряжениям.
Фактические напряжений определяли методом разгрузки на 5-ти горизонтах рудника «Акбакай»: на дне карьера -60 м и на горизонтах 120 м, 180 м, 240 м, 300 м. А на руднике Акжал в карьере глубиной 260–300 м и в нижних двух подземных горизонтах. Глубина скважин в пределах 5,5–7,0 м и производились по три измерении с каждой скважины. Измерение напряжений было выполнено на 12 участках рудника Акбакай и 9 участках на руднике Акжал. На каждом участке измерения производились в трех направлениях. Таким образом на этих рудниках для определении напряжений в массиве горных пород было реализовано 63 замеров. В таблице приведены обобщенные результаты измерения естественных напряжений кварцитах Акбакайского и в известняках Акжалского месторождений [7].
Результаты и обсуждение
Анализируя таблицу 1 и полученные по другим рудникам результаты определения естественных напряжений, нельзя не заметить следующих особенностей распределения горизонтальных напряжений в породных массивах.
Таблица 1
Р езультаты измерения естественных напряжений на месторождении Акбакай
|
Место измерения, горизонт |
Глубина от дневной поверхности, Н. м |
Средние значения напряжений, МПа |
Сумма горизонтальных напряжений (х+у),МПа |
||
|
х |
у |
z=Н |
|||
|
Карьер |
60 60 |
5,2 5,0 |
3,3 3,2 |
2,2 2,0 |
8,5 8,2 |
|
2-гор. |
120 120 |
7,8 6,3 |
4,4 5,7 |
3,3 3,5 |
12,2 12,0 |
|
3-гор. |
180 180 |
9,1 10.5 |
6,6 5,1 |
5,4 5,2 |
15,7 15,6 |
|
4-гор. |
240 240 240 |
12,1 14,0 13,7 |
7,1 5,1 5,3 |
6,7 7,2 6,8 |
19,2 19,1 19,0 |
|
5-гор. |
300 300 300 |
12,2 14,0 13,8 |
10,4 9,0 8,8 |
8,6 8,2 8.5 |
22,6 23,0 22,6 |
|
Результаты измерения естественных напряжений на месторождении Акжал |
|||||
|
Карьер |
260 280 300 |
8,6 9,0 10,2 |
6,3 6,5 7,3 |
4,1 4,2 5,0 |
14,9 15,6 17.5 |
|
1-гор. |
460 460 460 |
14,8 17,1 18.5 |
10,4 8,6 7,3 |
4,3 5,8 6,0 |
25,2 25,7 25,8 |
|
2-гор. |
500 500 500 |
20,1 20,5 20,7 |
10,1 10,6 10,7 |
6,7 7,2 6,8 |
30,2 31,1 31,4 |
Примечание: z — среднее значение напряжения, действующего в вертикальном направлении; х– среднее значение нормального напряжения, действующего в меридиональном направлении; у — среднее значение нормального напряжения, действующего в широтном направлении.
Во-первых, горизонтальные напряжения по своим значениям превосходит вертикальные, во-вторых, на равных глубинах от дневной поверохности в крепких породах горизонтальные напряжения имеют более высокие значения, чем относительно слабых, в-третьих, вертикальные напряжения в среднем бизки к значению Н независимо от прочности горной породы.
Таким образом, все виды напряжений с глубиной меняются, особенно сумма значении горизонтальных напряжений (х+у) меняется по определенной закономерности и, это хорошо видно из рисунка 1.
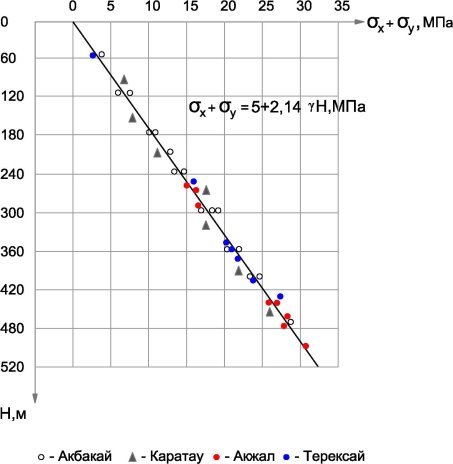
Рис. 1. Изменение суммы горизонтальных напряжений (х+у) с глубиной
Согласно рисунку, связь между напряжением и глубиной считать прямолинейной, то корреляционная связь определяется по следующей формуле
У= а + в . Х, (4)
где У– сумма главных горизонтальных напряжений, (х+у); Х — глубина горных работ, Н; а и в — параметры уравнений.
Результаты вычислений параметров приведены в таблице 2.
Таблица 2
Таблица корреляционной зависимости между глубиной горных работ (Н) и главных горизонтальных напряжений (х+у) по руднику Акбакай
|
Горизонт |
Н, м |
(х+у) |
Х н |
У |
Х н У |
Х н 2 |
У 2 |
|
1 Карьер |
60 60 |
8,5 8,2 |
0,6 0,6 |
0,09 0,08 |
0,05 0,05 |
0,36 0,36 |
0,001 0,001 |
|
2 |
120 120 |
12,2 12,0 |
1,2 1,2 |
0,12 0,12 |
0.14 0,14 |
1,44 1,44 |
0,01 0,01 |
|
3 |
180 180 |
15,8 15,6 |
1,8 1.9 |
0,16 0,16 |
0,29 0,29 |
3,24 3,24 |
0,02 0,02 |
|
4 |
240 240 240 |
19,2 19,1 19,0 |
2,4 2,4 2,4 |
0,19 0,19 0,19 |
0,46 0,46 0,46 |
5,76 5,76 5,76 |
0,03 0,03 0,03 |
|
5 |
300 300 300 |
22,6 23,6 22,7 |
3,0 3,0 3.0 |
0,23 0,23 0,23 |
0,69 0,69 0,69 |
9,0 9,0 9,0 |
0,05 0,05 0.05 |
|
|
Нср. = 234,0 |
орт = 194,0 |
Х = 23,4 |
У = 1,94 |
(Х . У) =4,41 |
Х 2 = 54,36 |
У 2 = 0,34 |
Параметр — в линейной с вязи определяется по формуле
в =
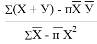
где п- число измерений.
П
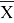
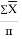
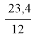
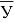
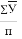
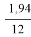
Тогда
в
=

А значение парметра а определяется из выражения (4):
а
= У — в.Х = 19,4–0,06
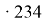
следовательно У= 5 + 0,06 Н
или х+у= 5+0,06
Если обратить внимание на формулу (1), то нормальные напряжения имеют также связь с объемным весом пород. Тогда формула (6) будет иметь следующий вид:
х+у= 5+2,14 Н, МПа (7)
где -объемный вес породы 2,8 10–2,МПа/м
Н — глубина от дневной поверхности, м.
Коэффициент корреляции связи равен
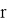
Естественно было стремление сравнить полученные нами результаты по напряжениям с результатами аналогичных работ других исследователей. По литературным материалам нам удалось собрать данные по рудникам, расположенным в пределах горно-складчатых структур. Анализ собранных данных по напряжениям в массивах горных пород в различных регионах был увязан с типом их тектонической структурой. Например, приведенные на рисунке 2 данные по рудникам Каратау, Акбакай (Казахстан), Терексай Кыргызской республики тесно согласуются с данными, полученными на руднике Акжал [8].
По итогам изучения напряженно-деформированного состояния породного массива месторождения Акжал можно сделать следующие выводы:
- Установлено, что значения горизонтальных напряжений превышают вертикальных 1,2–1,5 раза.
- Получена графоаналитическая зависимость горизонтальных напряжений от глубины, т. е. ху= f(Н).
-
Полученные результаты сравнивались с результатами аналогичных работ других авторов, и они позволяют сделать вывод о достаточной высокой надежности полученных уравнений регрессии (коэффициент корреляции
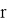
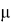
Литература:
- Heim A. Mechanism us der Gebirgebildung, Bale, 1878.
- Динник А. Н. О давлении горных пород и расчет крепи круглой шахты.- Инженерный работник, 1925, № 7. — С.1–12.
- Методические указания по постановке исследований сдвижения горных пород на моделях. — Л.: ВНИМИ, 1974.- 65с.
- Руководство по измерении ю напряжений в массиве скальных пород методом разргузки (И. А. Турчанинов, В. И. Иванов и др.).-Апатиты; Изд-во КФ АН С ССР, 1980. — 47 с.
- Патент на полезную модель № 1607. Ультрозвуковой способ определения нарушенности массива /Нурпеисова М. Б., Бек А. А. и др.-Астана, 2016
- Патент на полезную модель № 1885. Способ прогнозирования НДС массива горных пород /Айтказинова Ш. К., Доненбаева Н. С., Дербисов К. Н.-Астана, 2020.
- Nurpeisova M. B., Aitkasinova Sh.K. Kirgisbaeva G. M. Geomechanikal monitoring of the massif of rocks at the combined wav of defeopment of fields // Geodesy &Mine Surveying 14 th International Multidisciplinary Scientific GeoConference SGEM. –Болгария, Альбена, 2014.- Р. 279–292. (База Scopus)
- Nurpeisova M., Donenbaeva N.. Devepolment of Geodetic Methods of Monitoring of OpenPit Sides Stability // Bioscience Biotechnology Research Special issue volume 12 number, September 2019, Print ISSN: 0974–6455, Page 67–78.







