Разработка технологии отслеживания летательных аппаратов в условиях неопределенностей



Введение. В последнее время все чаще вызывает интерес улучшение способов наблюдения за небом. Это связано, в основном, с тем, что количество летательных аппаратов очень быстро растет. За всеми ними необходимо слежение, чтобы обеспечить безопасность воздушного пространства. Еще некоторое время назад для наблюдения за самолетами использовались радиолокаторы, которые могли получать только расстояние до фюзеляжа самолета. В последнее время, в российские аэропортах активно внедряются многопозиционные системы наблюдения. Их очень важное отличительное свойство — они передают по каналам связи диспетчеру не только информацию о местонахождении самолета, но и данные о количестве пассажиров, барометрической высоте и так далее. Казалось бы, что задача наблюдения за небом не такая уж и сложная, и все дело только в локаторах. К сожалению, это не так. Количество самолетов, ожидающих посадки, а также просто пролетающих над любым аэропортом, велико. Если принять во внимание ту информацию, который каждый из самолетов передает на обработку — данных получается слишком много, что приводит к сильно загруженным каналам связи [1]. Также из-за рельефа местности, не говоря уже о произвольных помехах, некоторые станции не могут точно определить местонахождении самолета и передают в центр обработки заведомо ложную информацию, а при несовпадении данных с нескольких датчиков процесс вычисления расположения самолета повторяется заново. Этот процесс необходимо модернизировать, что и будет реализовано в этой работе.

В основе работы лежит одновременное использование таких подходов, как рандомизация [2] и мультиагентные технологии [3, 4, 5]. Традиционный подход к процессу создания самых разнообразных систем представляет собой выполнение детерминированных алгоритмов, а во многих практических приложениях механический перенос на сложные системы естественных подходов, работоспособных для простых задач, приводит к неразрешимым противоречиям. Включение рандомизации позволит обобщить традиционные подходы [6]. В литературе, как правило, рассматриваются неопределенности, обладающие некоторыми заданными нормальными статистическими свойствами. Задачи обучения и адаптивного управления значительно усложняются при рассмотрении произвольных внешних по отношению к системе неопределенностей (например, при ограниченных, но в остальном неизвестных) [7]. В этой работе будут исследованы именно такие помехи, так как с ними чаще всего сталкиваются на практике. Мультиагентные технологии, в свою очередь, позволят естественным образом перейти к распределенным алгоритмам решения задач, что становится актуальным в связи с быстрым ростом количества летательных аппаратов.

Постановка задачи. Пусть существует распределенная сеть, состоящая из летательных аппаратов и датчиков слежения за ними (сенсоров). Введем обозначения: — набор всех сенсоров, — набор всех целей, — размерность пространства,

— множество координат сенсора в момент времени ,, — множество координат цели в момент времени — общий вектор состояния всех целей в момент времени . Предположим, что сенсоры могут обмениваться друг с другом информацией о местоположении целей согласно заранее известной топологии сети. — матрица связности в момент времени . Пусть в каждый момент времени сенсор

измеряет квадрат расстояния только до одной цели . Предположим, что он еще получает квадрат расстояния от других сенсоров до этой же цели. Стоит отметить, что количество соседей заранее задано и обосновано ограничениями на топологию сети. Обозначим через набор соседей, с которыми сенсоер наблюдает за целью . Необходимо найти такой общий вектор оценок местоположения состояния целей , который будет практически совпадать с .

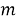
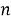
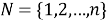
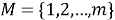
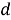
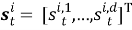
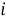
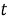
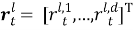
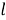
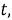
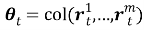
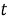
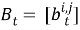
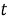
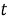
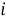
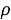
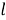
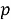
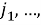
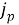
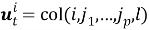
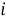
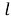
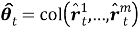
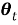
Алгоритм решения. Точное местоположение цели можно выразить как:

, (1)

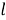
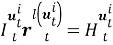
где , , , , , — последний элемент вектора

, и обозначают транспонированную и псевдообратную матрицы, соответственно.

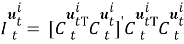
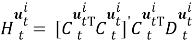
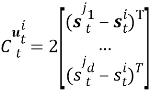
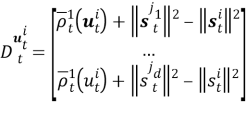
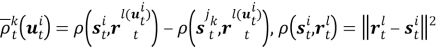
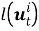
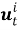
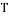
Пусть сенсоры получают наблюдения с помехами:

,(2)

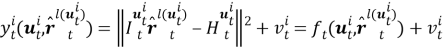
где — неизвестные, но ограниченные по амплитуде помехи [7], а обозначает оценку величины.

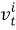
Пусть задано вероятностное пространство ( ), соответствующее произвольному множеству

с -алгеброй всех событий и вероятностной мерой . Обозначим -алгебру всех вероятностных событий, которые произошли до времени , как . Пусть — условное математическое ожидание относительно -алгебры . Для того, чтобы определить точное местоположение цели, необходимо минимизировать введенную ранее в выражении (2) функцию потерь [8]:

. (3)

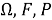
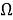
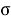
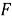
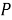
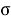
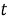
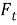
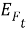
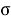
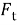
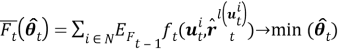
Распределенный мультиагентный алгоритм, которым решается задача оптимизации (3), совмещает в себе два подхода, а именно SPSA (simultaneous perturbation stochastic approximation) [9] и LVP (local voting protocol) [10]. Согласно этому алгоритму определение местоположения объекта наблюдения можно произвести по формулам:

, (4)

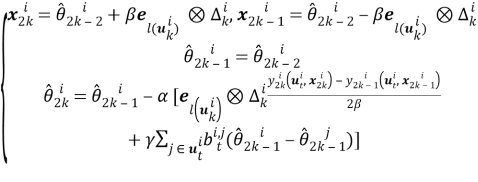
где — параметры алгоритма; — общий вектор оценок состояния всех целей, полученных сенсором ; — выбранные оценки местоположения объекта, значения которых определяются с использованием оценок ; принимает значения

согласно распределению Бернулли с вероятностью 0,5; — вектор, в котором все элементы нули, кроме -го ряда, — шаг алгоритма.

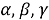
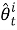
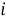
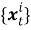
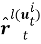
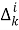
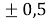
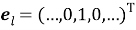
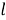
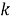
Заключение. В настоящей работе рассмотрен алгоритм для отслеживания большого количества летательных аппаратов в условиях влияния произвольных, но ограниченных по амплитуде помех при измерении их местоположения.

Исследование проводится при поддержке Фонда содействия инновациям по договору № 397ГУЦЭС8-D3/56404 от 2019 г.

Литература:

1. Oh, S., Hwang, I., and Sastry, S. (2008). Distributed multitarget tracking and identity management. Journal of Guidance, Control, and Dynamics, 31(1), 12–29.
2. Spall, J.C. (1992). Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Transactions on Automatic Control, 37(3), 332–341.
3. Olfati-Saber, R., Fax, J., and Murray, R. (2007). Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE, 95(1), 215–233.
4. Olfati-Saber, R. and Murray, R.M. (2004). Consensus problems in networks of agents with switching topology and time-delays. IEEE Transactions on automatic control, 49(9), 1520–1533.
5. Proskurnikov, A. and Tempo, R. (2018). A tutorial on modeling and analysis of dynamic social networks. Part II. Annual Reviews in Control, 45. 166–190.
6. Граничин, О. Н. Круглый стол «самоорганизация и искусственный интеллект в группе автономных роботов: методология, теория, практика» / О. Н. Граничин // Стохастическая оптимизация в информатике. — 2020. — № 16/1. — С. 5–12.
7. Granichin, O. and Amelina, N. (2015). Simultaneous perturbation stochastic approximation for tracking under unknown but bounded disturbances. IEEE Transactions on Automatic Control, 60(6), 1653–1658.
8. Erofeeva, V., Granichin, O., Ivanskiy, Y., and Jiang, Y. (2019). Distributed tracking based on simultaneous perturbation stochastic approximation-based consensus algorithm. In Proceedings of the 58th IEEE Conference on Decision and Control, December 10–13, Nice, France. IEEE.
9. Amelina, N., Granichin, O., Granichina, O., and Jiang, Y. (2014). Differentiated consensuses in decentralized load balancing problem with randomized topology, noise, and delays. In 53rd IEEE Conference on Decision and Control, 6969–6974. IEEE.
10. Amelina, N., Fradkov, A., Jiang, Y., and Vergados, D.J. (2015). Approximate consensus in stochastic networks with application to load balancing. IEEE Transactions on Information Theory, 61(4), 1739–1752.