В рамках этой работы было проведено исследование проблематики сохранения качества цифровой информации при использовании метода сжатия данных Хаффмана. В этой работе была полностью описана специфика этого метода, вместе с его основными преимуществами.
Ключевые слова: цифровые данные, информация, методика сжатия цифровой информации, метод сжатия Хаффмана, методик сжатия информации без потери качества.
Стоит отметить, что современный мир остро нуждается в разработке и практическом использовании продвинутых методов сжатия цифровой информации. Конечно, сейчас человечество имеет доступ не только к хранилищам цифровых данных огромного объема, но и к высокоскоростным способам обмена информацией. При этом, нужно учесть, что постоянно наблюдается рост объемов передачи данных. Ранее вполне нормальным было смотреть фильмы, записанные на обычном компакт-диске, вмещающем в себя 700 мегабайт информации. Теперь же при просмотре онлайн-фильмов в высоком качестве, видеоряд может занимать несколько десятков гигабайт пространства. Безусловно для обеспечения возможности хранения такого огромного объема информации и ее передачи потребуется не только время и широкий канал передачи информации, но и большое хранилище цифровых данных. Для реализации этих задач как раз-таки и применяются различные методики сжатия информации. В рамках этой статьи будет изучен принцип работы методов сжатия цифровой информации без потери ее качества. Также мы попробуем понять, как работает самый популярный метод сжатия данных под названием «алгоритм Хаффмана».
Процесс сжатия объема цифровой информации имеет выраженный алгоритмический характер. Он основан на принципе сокращение избыточности объемов данных. Метод сжатия информации предполагает уменьшение ее объема без ее утери. [1, с. 214]
В основе алгоритма Хаффмана лежит элементарная концепция. В рамках этого алгоритма применяется метод, предполагающий кодирование одинаковых символом меньшим количеством бит, чем тех символов, что встречаются не так часто.
Подобный метод сжатия цифровой информации был разработан в 1952 году Д. А. Хаффманом. При этом в то время еще не было никаких компьютеров современного типа. За счет эффективности этого метода он был положен в различные современные способы сжатия цифровых данных путем применения специальных кодировочных алгоритмов.
В основе идеи алгоритма лежит следующий принцип: при наличии знаний о вероятности наличия в сообщении конкретных символов, возникает возможность описания формирования кодов с переменной длиной, которые будут структурно представлять собой цельные количества битов. Короткие коды присваиваются тем символам, которые встречаются чаще. У кодов Хаффмана есть свой индивидуальный префикс, что дает возможность их декодировки даже несмотря на то, что их длина имеет переменный характер.
При использовании динамического алгоритма, разработанного Хаффманом, можно будет получить на входе частотную таблицу символов, которые встречаются в конкретном сообщении. На следующем этапе на основе данной таблицы происходит построение кодировочного дерева Хаффмана.
На сегодняшний день применяются два способа сжатия цифровой информации: с потерями части данных и без каких-либо потерь. При использовании метода сжатия информации с потерями восстановленная информация будет несколько отличаться от изначальной, что приводит к падению ее качества. Этот способ применим в тех случаях, когда при восстановлении цифровой информации не требуется максимальная точность. Если же используется способ сжатия без потерь, тогда восстановленные данные будут иметь свой исходный вид. Подобный метод, как правило, применяется при передачи текстовых цифровых документов. В дальнейшем в рамках этой работы будет проводиться работа по изучению второго способа сжатия цифровой информации. [2, с. 364]
Методика сжатия цифровой информации без потерь использует алгоритм уменьшения битов за счет определения и последующего удаления обнаруженной избыточности статистического характера. Для того, чтоб понять принцип работы этого способа, потребуется ознакомиться с некоторыми следующими примерами. [4, с. 163]
Предположим, у нас есть набор из девяти фигур круглой формы. Три красных, три голубых и три коричневых круга. При этом, вместо того, чтоб показывать все девять кругов можно просто оставить три круга разного цвета и указать рядом с ними количество этих кругов. Фактически, мы предоставляем аналогичную информацию, но уже меньшего объема.
В качестве еще одного примера можно взять файл, содержащий в себе следующий текст: RRRRRZZZZEEEGGGGGG.
Данная текстовая информация с помощью методики Хаффмана может быть сжата следующим образом: R5Z4E3G6. В итоге вместо 18 символов нам для предоставления аналогичной информации потребовалось всего 8. При этом, может показаться, что этот метод сжатия данных работает слишком безукоризненно, что сложно себе представить. По сути, во многом, сама концепция сжатия информации без потерь, идет в разрез Ньютоновским физическим законам.
Правда, все же этот метод действительно идеально работает. Современные программы, использующиеся для сжатия информации без потерь, обеспечивают это за счет использования таких эффективных алгоритмов, как алгоритм Хаффмана, а также кодирование LZW. [4, с. 241]
Особенности алгоритма Хаффмана
В основе популярности этого метода сжатия цифровой информации лежит его простота и легкость применения. Несмотря на то, что сама методика была придумана еще в середине 20-го века, она до сих пор сохраняет свою актуальность. В основе работы алгоритма Хаффмана лежит принцип того, что в цифровой информации одни символы могут встречаться намного чаще других. При этом потребуется найти самые часто встречающиеся символы и присвоить ими короткую кодировку. При этом самые редкие символы получают, наоборот, длинный код. В рамках алгоритма Хаффмана на входе должна находиться изначально сформированная частотная таблица, без которой сам метод попросту не будет работать. [2, с. 75]
Алгоритм сжатия информации задается частотной таблицей. Изначально определяется пара информационных узлов с самой низкой частотой символов. После этого формируется родитель, который будет равен сумме частот. При этом родитель будет выступать в качестве нового полноценного узла, который придет на замену двум предыдущим узлам. Дуге, выходящей от родителя, присваивается бит с нулем или единицей. Данная операция повторно осуществляется до момента пока внутри списка не будет сформирован один единственный узел. К примеру, мы имеем следующую частотную табличку:

Исходя из специфики используемого алгоритма, потребуется провести работу по суммированию пары узлов, имеющих самую низкую частотность:
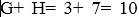
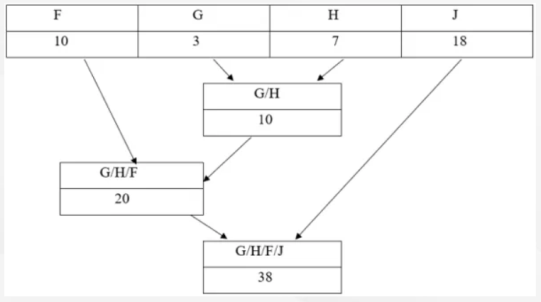
На следующем этапе каждому символу присваивается уникальный код. Для этой цели нужно будет продвигаться по направлению снизу вверх по кодировочному древу. При этом нужно будет копить биты в процессе движения по веткам древа. Движение вправо это ноль бит, а влево один бит. В итоге на выходе будет получена таблица следующего вида:

У этого алгоритма есть один серьезный недостаток, заключающийся в том, что декодеру для восстановления информации нужно будет иметь данные о частотной таблице. В итоге размер полученного файла будет увеличен по причине размещения перед кодом частотной таблицы. Также нужно отметить, что факт наличия полноценной частотной таблицы Кроме того, факт наличия перед кодировочным кодом полноценной частотной таблицы диктует необходимость двойной проходки по сообщению с целью формирования самой модели информации и для ее последующего декодирования. [5, с. 152]
Несмотря на то, что алгоритм Хаффмана был разработан более 60 лет назад, он до сих пор сохранил свою актуальность. Поэтому он в том или ином виде используется современными программами, обеспечивающими возможность сжатия данных без их потери.
В рамках данной статьи была проведена работа по описанию способов сжатия цифровой информации без ее потери, а также был описан самый популярный алгоритм Хаффмана. При этом, важно отметить, что существуют самые разные алгоритмы, обеспечивающие возможность сжатия данных без потерь. Поэтому пользователю нужно будет самостоятельно выбирать наиболее подходящий для себя способ.
Литература:
- Баринов В. В. Сжатие данных, речи, звука и изображений в телекоммуникационных системах, РадиоСофт — Москва, 2019. — 360 c.
- Вотолин Д. Ратушпяк А. Смирнов М. Юкин В. Методы сжатия данных. Устройство архиваторов, Сжатие изображений и видео. — М.:ДИАЛОГ-МИФИ, 2018 г. — 381 с.
- Рассел Джесси Сжатие данных, Книга по Требованию — Москва, 2017. — 104 c.
- Ратушняк О. А. Сжатие мультимедийной информации. // Hard'n'Soft. 2016. — №.4 — стр. 78–79.
- Сэломон Д. Сжатие данных, изображений и звука, Техносфера — Москва, 2016. — 368 c.







