Развитие исследовательских компетенций у учащихся на уроках математики при применении практико-ориентированного подхода в обучении



Роль образования для развития творческих способностей личности неоценима. Особенно важна роль математики. Важнейшим средством формирования у школьников высокой математической культуры, активизации обучения математике является эффективная организация и управление учебной деятельностью в процессе решения различных математических задач.

В ФГОС сказано, что «методологической основой Стандарта является системно-деятельностный подход, который обеспечивает: формирование готовности обучающихся к саморазвитию и непрерывному образованию; … активную учебно-познавательную деятельность обучающихся…» [5].

В Системно-деятельностном подходе основные результаты обучения и воспитания выделяются в контексте ключевых задач и универсальных учебных действий, которыми должны владеть учащиеся. [3].

Развитие личности школьника в системе образования обеспечивается, прежде всего, через формирование универсальных учебных действий, которые выступают основой образовательного и воспитательного процесса. Овладение учащимися универсальными учебными действиями создают возможность самостоятельного успешного усвоения новых знаний, умений и компетентностей, включая организацию усвоения, то есть умения учиться. Эта возможность обеспечивается тем, что универсальные учебные действия — это обобщенные действия, порождающие широкую ориентацию обучающихся в различных предметных областях познания и мотивацию к обучению.

Требования о переходе к системно-деятельностному подходу в образовании возникли в связи с необходимостью привести образование в соответствие с потребностями рынка труда. С введением этого подхода в систему образования становится возможным на ранних этапах готовить целенаправленно качественных специалистов. Все более очевидной становится потребность оценивать результаты педагогического образования, не ограничиваясь качеством знаний.

Компетентностный подход, входящий в системно-деятельностный подход позволяет моделировать результаты обучения и их представления как нормы качества образования.

Такой подход акцентирует внимание на результате образования, причем в качестве результата рассматривается не сумма усвоенной информации, а способность учащихся действовать в различных проблемных ситуациях , то есть основными единицами оценки качества результата обучения выступают компетентности и компетенции.

Рассматривая этот вопрос у различных авторов в работах Э. Ф. Зеера и Э. Э. Сыманюк, И. А. Зимней, Ю. Н. Емельянов, Л. И. Анцыферова мы сталкиваемся с неоднозначностью трактовки самих понятий «компетенция» и «компетентность» и с проблемой соотношения этих понятий.

Ряд авторов рассматривает компетентности (компетенции) как составляющие части общей компетентности человека (специалиста). Так, например [3].

Известна позиция А. В. Хуторского, который предлагает под компетенцией понимать «некое отчужденное, наперед заданное требование к образовательной подготовке учащегося», а термин «компетентность» использовать для фиксирования уже состоявшихся качеств личности, «владения, обладания человеком соответствующей компетентностью, включающей его личностное отношение к ней и предмету деятельности» [6].

Из вышеизложенного делаем вывод^ компетенция и компетентность — это разные понятия, компетентность включает в себя разного рода компетенции, то есть является более широким понятием. Понятия компетенций, компетентностей значительно шире, чем понятия знаний, умений, навыков, так как включают в себя ещё и направленность личности (способность преодолевать стереотипы, чувствовать проблемы, проявлять проницательность, гибкость мышления; характер — самостоятельность, целеустремленность, волевые качества и т. п.).

Рассмотрев этот теоретический вопрос, пред учителями стоит задача преобразовать учебный процесс и его компоненты. На уроках математики это позволят сделать подбор задач со специфической фабулой, которые помогают в развитии исследовательских компетенций.

Нередко случается так, что, решая практические задачи в совершенно разных отраслях, специалисты приходят к одной и той же математической модели.

Возьмем, например, способ нахождения наибольших и наименьших значений функции с помощью производной, данный метод активно применяется для решения множества практических задач, возникающих в разных отраслях человеческой деятельности. На сегодняшнее время, в частности в связи с научно-техническим прогрессом, применение дифференциального исчисления становится все более актуальным для специалистов.

Из выше сказанного мы видим, что при прохождении различных тем, на уроках можно решать не просто задачи из учебника, а выбирать именно практико-ориентированные задания.

Приведём примеры таких заданий из темы Производные :

1. Требуется вырыть канал прямоугольного сечения, глубиной 1 м. При какой ширине канал будет иметь гидравлически наивыгоднейший профиль? [6].

Рис. 1

Найдем, при каком отношении глубины канала к ширине, канал будет иметь гидравлически наивыгоднейший профиль. Пусть — ширина канала,

— его живое сечение, — смоченный периметр . Тогда глубина канала , а его смоченный периметр (рис. 1):

. Требуется найти наименьшее значение функции на промежутке . Найдем производную:

Так как при и

при , таким образом, функция в точке достигает наименьшего значения.

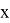
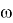
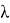
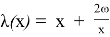
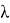
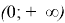
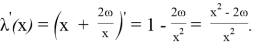
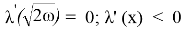
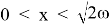
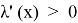
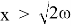
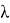
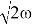
Итак, ширина канала в рассматриваемом случае должна быть , глубина , а искомое отношение равно . То есть, при глубине канала в 1 м, наиболее оптимальная ширина b равна: м

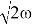
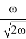
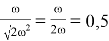
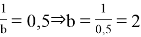
2.Необходимо проложить канал, сечение которого — сегмент (рис. 2). Каким должен быть центральный угол , чтобы канал имел гидравлически наивыгоднейший профиль?

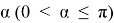
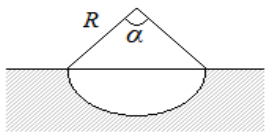
Рис. 2

Пусть R — радиус круга. Живое сечение канала найдем как разность площадей сектора и треугольника:

. Отсюда получаем, что

; , и значит, смоченный периметр равен:

.

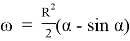
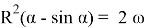
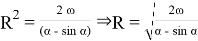
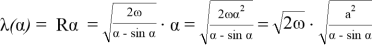
Исследуем более простую функцию . При имеем

. Так как и на рассматриваемом интервале, то производная на определена и отрицательна. Поэтому функция

, а значит, и убывает на . Следовательно, функция достигает наименьшего значения при . В сечении канала должен быть полукруг.

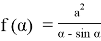
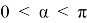
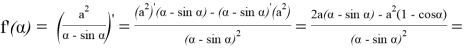
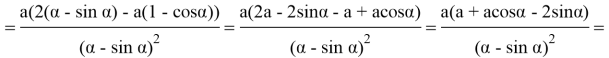
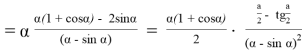
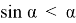
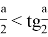
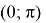
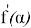
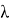
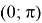
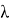
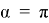
3. С помощью измерительных приборов было выявлено, что высота Эвереста над городом Катманду составляет 5768 м, пользуясь этими данными нужно определить высоту ландшафтного превышения Эвереста над Катманду, если расстояние между ними ≈ 150 км.

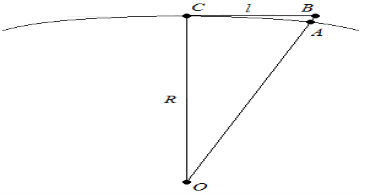
Рис. 3

Высота превышения Эвереста над Катманду равна сумме значений, полученных с помощью измерительных приборов и дополнительной поправки на кривизну земли

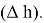
Определим значение той самой дополнительной поправки. Рассмотрим рис.1, на котором изображена поверхность океана, где точка O — центр Земли. Пусть точка C лежит на поверхности, а точка B принадлежит горизонтальной плоскости (проходящей через точку C по касательной Земли). В таком случае, так как угол между лучом CB и горизонтальным направлением равен нулю, то, глядя из точки C , нам покажется, что B и C находятся на одном уровне. Поэтому, мы допустим поправку на кривизну Земли:

где

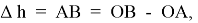
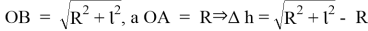
Величина Ɩ относительно мала по сравнению с величиной R . Поэтому для вычисления можно воспользоваться приближенной формулой , полученной (с помощью производной) из учебника «Алгебра и начало анализа 10–11класса». [5] Положив в этой формуле , , мы получим указанное выше выражение для . [5]

;

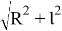
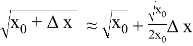
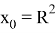
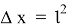
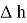
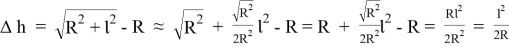
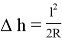
Подставляем имеющиеся значения в выведенную формулу и получаем (радиус земли берем 6 317 км):

км, то есть ландшафтное превышение Эвереста над Катманду составляет приблизительно 5768 м + 1781 м = 7549 м.

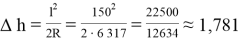
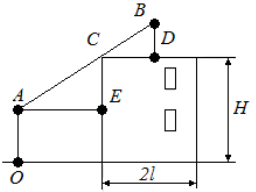
Рис. 4

4. Необходимо построить производственное здание с плоской крышей с высотой 9 м и шириной 6 м. С какой минимальной длинной стрелы крана возможно осуществить постройку (высоту автомобильного крана брать 2 м над землей).

Пусть высота здания — H, а ширина — 2Ɩ. Нам нужно найти длину стрелы крана всего до середины крыши (середину считаем по ширине) тогда кран достанет до любой точки здания.

Рассмотрим кран (рис. 4)., который, находясь в точке , дотягивается до середины крыши. Пусть угол наклона стрелы при этом составляет . Тогда

; ; ;

, где — высота подвеса стрелы крана. В таком случае длина стрелы (2).

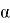
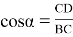
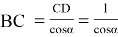
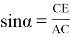
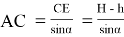
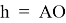
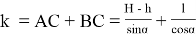
Из формулы (2) видно, что потребуется кран с другой длиной стрелы, так как при таком перемещении крана меняется угол α .

Определим наивыгоднейшее место установки крана (такое место, в котором крану понадобится стрела с наименьшей длиной). Для этого достаточно определить, при каком из промежутка функции принимает наименьшее значение. Найдем производную функции Ɩ:

. Рассуждая теперь так же, как и при решении задачи 2.2, находим, что функция достигает наименьшего значения при (3). Найдя из формулы (3) значение , которое равно и подставив в формулу (2), мы получим наименьшее возможное значение длины стрелы а именно

= .

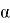
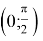
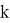
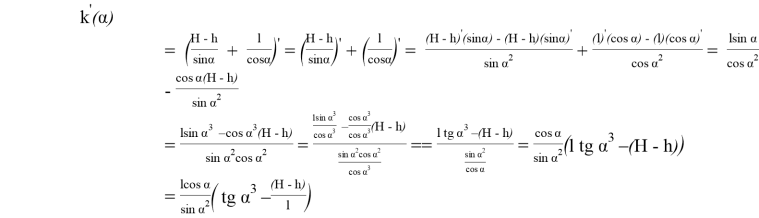
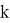
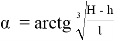
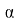
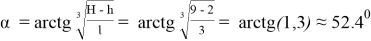
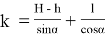
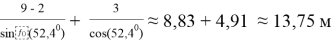
Как видно решение практико-ориентированных задач, проходит через применение исследовательских рассуждений, это позволяет учащимся пройти через основные этапы исследования, что способствует формированию их исследовательской компетенции.

Решая исследовательскую задачу, человек познает много нового: знакомится с новой ситуацией, описанной в задаче, с применением математической теории к ее решению, познает новый метод решения или новые теоретические разделы математики, необходимые для решения задачи. Исследовательские задачи создают условия для проявления творческой активности учащегося, выражающейся в стремлении познать объективно новые факты, используя теорию научных исследований. При решении исследовательских задач ученик обучается применять математические знания к практическим нуждам.

Литература:

1. Гребенюк, Е. В. Общекультурная компетентность современного учителя [Текст]: Е.В Гребенюк / Материалы конференции «Педагогическое образование в переходный период: результаты исследований 2010 года» / ГОУ ВПО «Российск государственный педагогический университет им. А. И. Герцена».- Санкт-Петербург: НИИ непрерывного педагогического образования, 2011
2. Золотовскова, А. А Психологические особенности СЛК [Текст]: курсовая работа / А.А Золотовскова/ руководитель: М. В. Кормильцева, Институт психологии, кафедра психологии профессионального развития — Екатеринбург 2009.-32 с.
3. Ильязова, М. Д. Компетентность, компетенция, квалификация — основные направления современных исследований [Текст] / М. Д Ильязова. // Профессиональное образование. Столица. — 2008. — № 1.
4. Мордкович А. Г. Алгебра и начало математического анализа, 10–11 классы, В 2 ч. Ч. 1. Учебник для учащихся общеобразоват. учреждений (профильный уровень)/А. Г. Мордкович. — 10-е изд., стер. — М.: Мнемозина, 2019. — 399 с.
5. Федеральный государственные образовательные стандарты среднего (полного) общего образования [Текст]: утверждён приказом Министерства образования и науки Российской Федерации от 7.06.2012.
6. Хуторской, А.В Ключевые компетенции и образовательные стандарты: [Текст]: доклад А. В. Хуторского на Отделении философии образования и теории педагогики РАО 23 апреля 2002 г. — Центр «Эйдос». [Электронный ресурс]. URL: www.eidos.ru/news/compet/htm.