В статье наглядно показана реализация функции потерь для тензорного потока регрессии через среднеквадратичную, среднюю абсолютную ошибку. Вычисление итогового значения нейронной сети через перекрестную энтропию и библиотеки numpy, tensorflow.
Ключевые слова: функция потерь, numpy, tensorflow, перекрестная энтропия.
Обычно в моделях машинного обучения мы собираемся предсказывать значения с учетом набора входных данных. Модель имеет набор весов и смещений, которые вы можете настроить на основе набора входных данных. Обучающие данные содержат несколько пар прогнозируемых и фактических значений. Для этого мы используем функцию потерь, чтобы определить, насколько прогнозируемые значения отличаются от фактических значений в обучающих данных. Мы можем обновить или изменить веса модели, чтобы минимизировать потери. У нас есть разные типы функций потерь: потери регрессии, классификационные потери. В регрессионных потерях: среднеквадратичная ошибка, средняя абсолютная ошибка, средняя ошибка смещения. В классификационных потерях: потеря петли или SVM, потеря кросс-энтропии.
Среднеквадратичная ошибка:
Математическая формулировка:
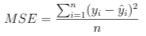
Как следует из названия, среднеквадратичная ошибка используется для измерения среднего квадрата разницы между предсказаниями и фактическими наблюдениями. Учитывайте только среднюю величину ошибки независимо от направления.
Средняя абсолютная ошибка:
Математическая формулировка:
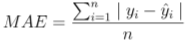
Средняя абсолютная ошибка измеряется как среднее значение суммы абсолютных различий между предсказаниями и фактическими наблюдениями. Он очень похож на MSE, измеряет величину ошибки без учета их направления. MAE более устойчив к выбросам, поэтому в нем не используется квадрат.
Средняя ошибка смещения:
Математическая формулировка:
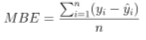
Ошибка среднего смещения гораздо реже встречается в приложениях машинного обучения. Это то же самое, что и MSE, но с той лишь разницей, что мы не берем абсолютные значения. Поэтому здесь следует проявлять осторожность, потому что положительные и отрицательные ошибки отменяют каждую прочее. Это повлияет на точность.
Потеря шарнира или потеря Svm:
Математическая формулировка:
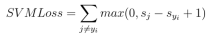
Потеря кросс-энтропии:
Математическая формулировка:
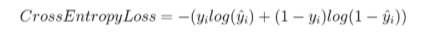
Это наиболее широко используемый в задачах классификации. Он увеличивает прогнозируемую вероятность.
В тензорном потоке аналогичной функцией потерь является функция l2_loss.
Теперь перейдем к другой функции потерь — кросс-энтропии. Это наиболее часто используемая функция в тензорном потоке. Здесь мы снова берем некоторые мнимые значения для фактических и прогнозируемых, и мы будем использовать numpy для математических вычислений. Softmax используется для преобразования ненормализованного в нормализованное и в распределение вероятностей.
Рис. 1. Вычисление значения numpy
Теперь давайте возьмем 2 примера:

Рис. 2. Примеры вычисления softmax_function
Теперь мы собираемся вычислить значение перекрестной энтропии для отдельных элементов (элемент — это скалярное значение). Первый параметр — это фактическое значение, а второй элемент — это прогнозируемое значение.

Рис. 3. Вычисление значения перекрестной энтропии
Фактическое значение и прогнозируемые значения находятся в векторах или списках, тогда мы можем вычислить перекрестную энтропию, взяв среднее значение поэлементных значений перекрестной энтропии.

Рис. 4. Программная реализация перекрестной энтропии
Обычно вероятности равны 0 или 1. Прогнозируемые вероятности softmax наблюдаются ранее. Эти прогнозируемые значения вычисляются на предыдущем уровне нейронной сети. Теперь примените softmax к логитам. Здесь логиты вычисляют значения в нейронных сетях перед применением softmax.
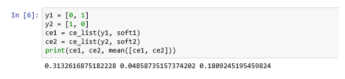
Рис. 5. Вычисление перекрестной энтропии
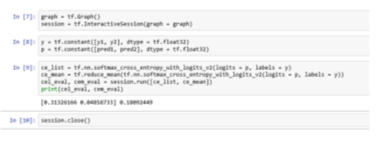
Рис. 6. Вычисление значений через функцию тензерного потока
Литература:
1. Nils J. Nilsson.Introduction to Machine Learning. Nils J. — Robotics Laboratory Department of Computer Science Stanford University, 1998
2. Yaser S. Abu-Mostafa, Malik Magdon-Ismail, Hsuan-Tien Lin. — Learning From Data Hardcover — January 1, 2012
3. Stuart Russell, Peter Norvig. Artificial Intelligence: A Modern Approach —Paperback — 5 Aug. 2013
- D. Michie, D. J. Spiegelhalter, C. C. Taylor. Machine Learning, Neural and Statistical Classification—January 1999







