В статье приводятся основные принципы и алгоритмы создания компьютерного изображения с помощью рейкастинга, а именно: графическое представление алгоритма броска луча и наложения текстур. Дана ссылка на полный исходный код проекта с инструкциями по его запуску.
Ключевые слова: raycasting, рейкастинг, псевдо 3D визуализация, graphic programming, графическое программирование, Wolfenstein.
Введение
Рейкастинг (англ. ray casting — бросание лучей) — один из методов рендеринга в компьютерной графике, при котором сцена строится на основе замеров пересечения лучей с визуализируемой поверхностью [1].
Термин впервые использовался в конце 70-х годов. Он применялся для описания метода параметрического моделирования с помощью комбинации примитивов, соединенных посредством операций объединения (+), разности (-) и пересечения (&).
В данной статье рейкастинг будет рассматриваться применительно к компьютерным играм. Конкретнее, будет рассмотрен способ отрисовки сцены в реальном времени в простейшей компьютерной игре.
Одной из первых игр, в которой была использована подобная технология псевдотрехмерной визуализации игрового пространства была Wolfenstein 3D (1992 год издания). Спустя почти 30 лет технологии визуализации в компьютерной графике, конечно, усложнились, однако, рейкастинг как технология имеет много общего с рейтрейсингом [2]. Рейтрейсинг, в свою очередь, благодаря увеличению вычислительных мощностей персональных компьютеров, в настоящее время становится современным способом визуализации некоторых объектов в играх, и уже довольно давно применяется в кинематографе для создания компьютерных спецэффектов.
Разработка своей собственной небольшой игры с применением технологии рейкастинга может помочь начинающим графическим программистам получить необходимый базовый опыт в создании компьютерных изображений и понимание того, какие аспекты программы наиболее сильно влияют на её производительность.
Основной принцип рейкастинга в играх
Принцип рейкастинга заключается в том, что от наблюдателя (точки, из которой мы будем смотреть на сцену) бросаются лучи в необходимую область перед наблюдателем — область видимости. Каждый луч, столкнувшись с препятствием луч запоминает расстояние, которое он пролетел в данном направлении, прежде чем встретил препятствие. В зависимости от этого расстояния мы можем визуализировать это препятствие (стену) на экране. Размер визуализируемого объекта выбирается в соответствии с необходимой перспективой. На рисунке 1 показано графическое представление этого процесса: в области примерно 60 перед наблюдателем бросаются лучи, каждый луч пролетает какое-то расстояние, и чем оно больше — тем меньше высота отображаемой стены.

Рис. 1. Визуализация рейкастинга
Далее будет описан общий алгоритм формирования таких изображений.
Соглашения для разработки собственной программы визуализации
− Представляемая сцена («карта») будет представлять собой двумерный массив символов. Символ «1» будет представлять препятствие, символ «0» — пустое пространство.
− Операционная система — Ubuntu.
− Для упрощенного создания графического окна воспользуемся надстройкой для Linux библиотеки LibX, MiniLibX.
Алгоритм отрисовки
Основной алгоритм отрисовки одной сцены заключается в следующем:
- Определить ширину экрана в точках
- Определить область видимости игрока в градусах (FOV — field of view)
- Определить шаг угла (область видимости, деленная на ширину экрана)
- Для каждого угла в интервале от 0 до FOV с полученным шагом выполнить бросок луча, и в зависимости от расстояния до препятствия отобразить вертикальную полоску на экране в соответствующей «колонке» дисплея
Основной алгоритм броска луча
Чтобы «бросить» луч необходимо вычислить расстояние между наблюдателем и препятствием в направлении луча. Если препятствие — это математический объект, который описывается каким-либо уравнением, а наблюдатель — точка на координатной плоскости, то чтобы рассчитать необходимое расстояние достаточно решить нужное уравнение. Однако, по нашим соглашениям препятствия — это «1» в двумерном массиве символов, поэтому нам нужно «шагать» лучом, пока мы не встретим стену.
Очевидным способом броска луча является перемещение начальной координаты луча в выбранном направлении на заданное константное расстояние [3] (рисунок 2).
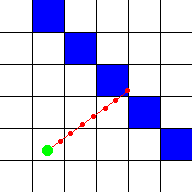
Рис. 2. Очевидное решение для броска луча
Однако, такое решение не является работоспособным для всех случаев. Основная причина в том, что под определенным углом луч будет проходить сквозь эту диагональную схему. Сокращение дистанции, на которую перемещается луч если и частично решает данную проблему, то вместе с этим сильно замедляет отрисовку изображения [3]. На рисунке 3 показан этот эффект.
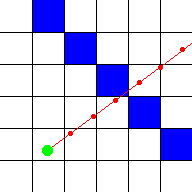
Рис. 3. Луч проскочил через стену
Правильным решением будет перемещать луч до следующей грани сетки. Это решение позволяет не нагружать отрисовку долгими вычислениями, и в тоже время позволяет не промахнутся мимо стены. Визуализация представлена на рисунке 4.
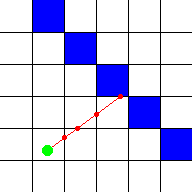
Рис. 4. Луч перемещается по граням сетки
Опираясь на эти идеи, мы можем реализовать алгоритм броска луча.
Примечание 1.
Перед отрисовкой стен мы можем нарисовать на экране линию горизонта и отделить «пол» от «потолка». Это поможет пользователям понимать, что верх и низ отличаются и сделать «игру» более красивой.
Примечание 2.
Поскольку мы проецируем изображение стены не на точку, из которой мы бросаем лучи, а на плоскость (монитор компьютера), то нам необходимо делать коррекцию расстояния до стен, чтобы убрать эффект рыбьего глаза. Необходимое расстояние до стены получается следующим образом:
length_to_wall = ray_distance * cos(cur_angle — midle_angle);
Здесь cur_angle — это угол текущей итерации относительно заданного FOV, а midle_angle — центральный угол FOV’а.
Примечание 3.
Для повышения эффективности алгоритма, вместо вычисления функции cos() во время отрисовки изображения можно заранее рассчитать таблицу косинусов и вместо вычисления косинусов брать заранее рассчитанное значение. Это может ускорить некоторые части программы в несколько раз [4].
Добавление текстур.
Поскольку бросаемый луч останавливается на грани сетки, то мы можем узнать точку попадания луча относительно одной клетки. Вычислив относительное расстояние от левого края клетки до места попадания луча, мы можем узнать соответствующий столбец пикселей изображения и вывести его на экран. Перед выводом, очевидно, этот столбик пикселей текстуры необходимо растянуть или сжать (в зависимости от высоты изображения и высоты препятствия, которое мы отображаем). Графически этот процесс представлен на рисунке 5 [5].
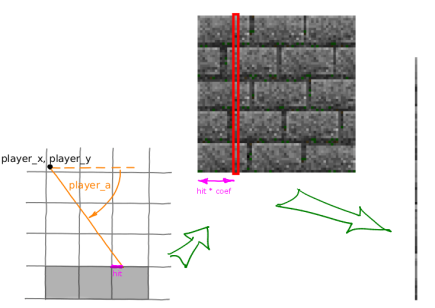
Рис. 5. Наложение текстур
Заключение
Результат программы представлен на рисунке 6. Полный исходный код проекта можно посмотреть в github репозитории автора [https://github.com/vesord/cub3d].

Рис. 6. Результат работы рейкастера
Изучение принципов рендеринга компьютерного изображения является первым шагом на карьерном пути графического программиста.
Литература:
- Рей кастинг. — Текст: электронный // Википедия свободная энциклопедия. — URL: https://ru.wikipedia.org/wiki/Ray_casting (дата обращения 05.12.2020)
- Boulos, Solomon (2005). Notes on efficient ray tracing // SIGGRAPH 2005
- Raycasting — Текст: электронный // Lode's Computer Graphics Tutorial. — URL: https://lodev.org/cgtutor/raycasting.html (дата обращения 07.12.2020)
- Евстратов В., Оценка скорости вычисления тригонометрических функций на Си / В. В. Евстратов // Молодой учёный № 46 (336) ноябрь 2020.
- Рейкастинг — Текст: электронный // Блог компании «Библиотека программиста». — URL: https://proglib.io/p/raycasting-for-the-smallest/ (дата обращения 08.12.2020)







