Рассмотрена структура и исследованы параметры нечетких систем управления на основе теории нечетких множеств. Получены результаты моделирования функции нечеткого контроллера и оценки его функциональности путем его моделирования в программе fuzzyTECH Explorer Edition.
Ключевые слова: нечеткое моделирование, нечеткий контроллер, микропроцессорная система, терм, функция принадлежности, fuzzy-система.
В настоящее время массовым становится применение так называемых нечетких систем управления под обозначением «fuzzy-системы». Большинство этих систем всецело входит в современный класс интеллектуальных систем управления (ИСУ). Fuzzy-системы строятся на теории нечеткой логики (нечетких множеств), разработанной профессором Лотфи Заде [1965, 7].
ИСУ рождаются на исследовательских платформах искусственного интеллекта и больших данных (Big Data), где объект управления (ОУ) по структуре сложен и по логике его параметры не поддаются точным методам классической теории автоматического управления. Для анализа структуры и свойств ИСУ необходима огромная обработка больших регистрированных данных как априорное представление информации разного формата о поведении исследуемой системы. Применение fuzzy-систем наглядно демонстрируется рисунком 1.
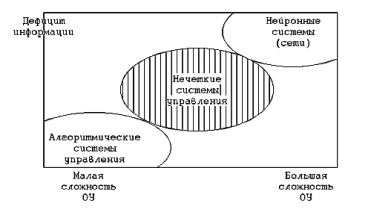
Рис. 1. Область применения нечетких систем управления
Принцип действия fuzzy-систем основан на применении свойств нечеткого логического вывода типа: «ЕСЛИ А…, ТО В…». Такие системы структурируются на базе знаний и элементах искусственного интеллекта. Обычно простейшее звено нечеткого управления содержит один восходящий нечеткий вывод (рисунок 2).
Схему вывода представим в виде:
Знание: «если Х есть А, то Н есть В».
Факт: «Х есть A’».
Вывод: «У есть В’».
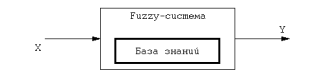
Рис. 2. Простейшее звено нечеткой системы
Здесь А, A’ и В, В’ — описание лингвистической переменной. Такое описание представляется в виде нечетких множеств m(A), m(B). Связь между входной переменной Х и соответствующей ей лингвистической переменной А может быть представлена в виде характеристической функции (рисунок 3). Характеристическая функция является лингвистической переменной класса «Высокий». Это обозначение является термом лингвистической переменной.
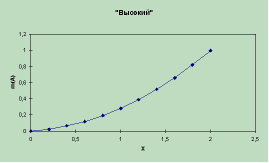
Рис. 3. Функция принадлежности лингвистической переменной «Высокий»
Здесь представленная функция имеет вид: А = (x i , a i ). Параметр x i принадлежит к Х. Переменная Х является элементами множества, a i — степенью принадлежности x i к множеству А. При дискретном представлении функции принадлежности А будет иметь вектор вида: А= (a 1 , a 2 ,..., a i ,... a m ), значения a i находится в интервале (0, 1). Аналогично B = (b 1 , b 2 ,..., b i ,... b m ), b i также находится в интервале (0, 1).
В нечетком логическом выводе А (это причина) и В (это есть результат) связаны матрицей R. Такая матрица отражает нечеткие причинно-следственные отношения между А и В. Матрицу R следует представить как:
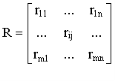
Профессор в своей теории Л. Заде определяет результат нечеткого вывода для параметра В’ [1]:
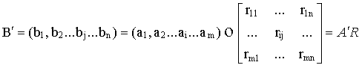
Из выражения (2) вытекает следующее выражение:
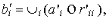
Здесь приняты обозначения:
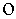
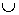
Другой теоретик нечеткого множества Мамдани предложил другой алгоритм нечеткого отношения, наиболее часто используемый на практике как [2]:
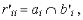
где

Реализация нечеткого управления в интеллектуальной системе управления с одним входом и одним нечетким выводом можно показать функциональной схемой с компенсационной емкостью (рисунок 4).
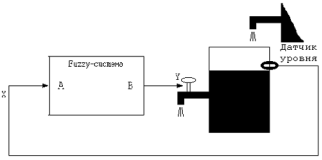
Рис. 4. Функциональная схема системы управления компенсационной емкостью
Такая система следит за протеканием вычислительного процесса, когда в компенсационной емкости должно быть достаточное количество жидкости. Значит, надо исключить ситуацию переполнения жидкости. Такая ИСУ отображает образ нечеткого вывода типа: «ЕСЛИ уровень «высокий», ТО открыть клапан К».
Таким образом, здесь входная лингвистическая переменная пишется как: А = «Высокий», выходная переменная В = «Открыть».
Функции принадлежности, связывающие физическую входную переменную «Уровень» в метрах с лингвистикой «Высокий» и выходную переменную «Угол поворота вентиля» с лингвистикой «Открыт» показаны соответственно на рисунке 5, а и 5, б.
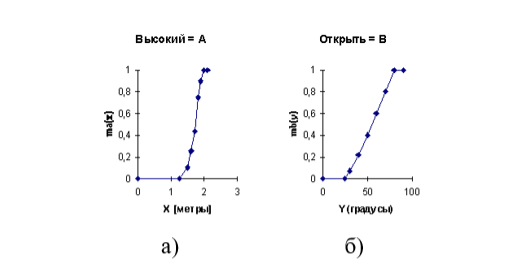
Рис. 5. Функции принадлежности «Высокий» и «Открыть»
По этим функциям входная и выходная переменные будут представлены в виде множеств:
«Высокий» = m A (x) = 0.1/1.5 + 0.3/1.6 + 0.7/1.7 + 0.8/1.8 + 0.9/1.9 + 1.0/2.0 + 1.0/2.1 + 1.0/2.2;
«Открыть» = m B (y) = 0.1/30° + 0.3/40° + 0.7/50° + 0.8/60° + 0.9/70° + 1.0/80° + 1.0/90°.
В итоге нечеткий вывод «Если высокий, то открыть» реализуется в нечеткой системе на основе формул (3) и (4). Эта реализация продемонстрирована на рисунке 6.
Управление происходит в 3 этапа:
– фаззификация — превращение датчика уровня (например, 1.75 м) в лингвистическую переменную (A’ — предельно высокий). На рисунке 6 это представлено в виде множества m A (x) с учетом разброса измеряемого параметра x;
– реализация нечеткого вывода по формуле:
b j ’ = И i (a i ’принадлежит a i ) b j .(5)
Этот процесс показан на рисунке 6, б и 6, в;
— дефаззификация — превращение выходного множества m B’ (y) в выходной сигнал вида y. На рисунке 6, в дефаззификация множества показана в виде реализации метода центра тяжести (фигуры, заштрихованной на рисунке 6, в). Значение сигнала y’ равно 70°.
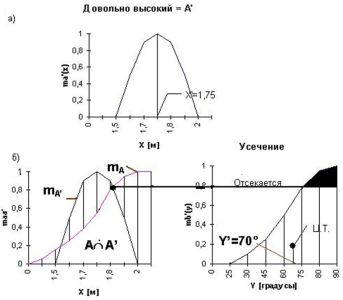
Рис. 6. Реализация принципа управления в fuzzy-системе
Нечеткое управление здесь может быть реализовано так называемыми нечеткими контроллерами. Такое устройство является машиной нечетких выводов (МНВ) [8], структура которой показана на рисунке 7.
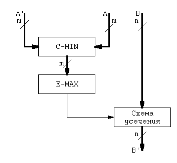
Рис. 7. Функциональная схема МНВ
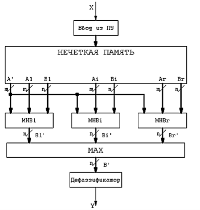
Рис. 8. Базовая архитектура нечеткого контроллера
Эта машина реализует нечеткий вывод вида: «ЕСЛИ А, ТО В» по формуле (5). Реализованный вывод указан на рисунке 6. Блок, реализующий функцию C-MIN, представляет пересечение множеств А и А’. Блок, реализующий функцию E-MAX, показывает из множества «А принадлежит А’» максимальный элемент с фиксированным значением. Такой процесс выполняет усечение множества В. Значит множество В превращается в множество В’.
Базовая архитектура нечеткого контроллера, реализующего нечеткие выводы (r), располагает r машинами нечетких выводов (рисунок 8). Кроме МНВ i базовый нечеткий контроллер располагает у себя нечеткую память. Здесь хранится база знаний и схема объединения результатов выводов.
Таким образом, нечеткое управление реализовано через обычные, так называемых специальное логико-арифметическое контроллеры. В таком контроллере нечеткие выводы генерируются вычислением значений выходного сигнала. Этот сигнал является лингвистической переменной и характеризуется через входные лингвистические переменные с операциями «И» и «ИЛИ». Переход от лингвистических переменных (термов) осуществляется через соответствующие характеристические функции, называемые функциями принадлежности (рисунок 9). Можно формулировать, что для реализации простейших алгоритмов нечеткого управления достаточно, чтобы лингвистические переменные содержали от 3 до 7 термов: например, Z-функция, p-функция, l-функция, S-функция.
Z-функция, p-функция, l-функция, S-функция

Рис. 9. Типовые функции принадлежности в нечеткой системе
Теперь можем с уверенностью представить, что разработка алгоритма нечеткого управления может содержать следующие 3 этапа:
Этап 1. Фаззификация — переход от физического значения к лингвистическим переменным и определение характеристических функций. Этот процесс осуществляется выполнением шагов:
Шаг 1. Для каждого терма лингвистической переменной определяется числовое значение физической величины (диапазоном значений). Такая величина лучше всего характеризует выбранный терм. Выбранным значениям присваивается характеристическое значение 1.
Шаг 2. Для терма выбирается диапазон значений физической переменной, где характеристическая функция имеет значение 0.
Шаг 3. После определения таких оптимальных значений выбирается промежуточные значения характеристических функций (рисунок 9).
Этап 2. Во втором этапе формулируются нечеткие правила. Нечеткие системы используют продукционные правила. Они удобны для описания зависимостей между лингвистическими переменными. Простое продукционное правило состоит из так называемого антецедента (ЕСЛИ...) и консеквента (ТО...) [6]. Антецедент содержит более одной посылки. В этом случае они объединяются через логику И или ИЛИ. Процесс формулировки нечеткого правила называется нечетким логическим выводом.
Процесс проходит в двух частях: обобщение и заключение. Например, для башенного крана (функциональная схема крана представлена на рисунке 10) входными переменными являются:
– расстояние от каретки до стены d [м];
– угол отклонения груза от вертикали j°.
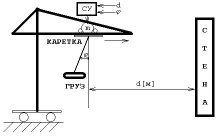
Рис. 10. Функциональная схема управления башенным краном
Для выходной переменной — мощность, подаваемая на двигатель каретки m. Теперь допустим, что каждая из этих переменных имеет 3 терма: нулевое, среднее и большое. Этим термам соответствуют свои характеристические величины:
– D 0 — нулевое (малое) расстояние;
– D ср — среднее расстояние;
– D б — большое расстояние;
– j 0 — нулевой (малый) угол;
– j ср — средний угол;
– j б — большой угол;
– М 0 — нулевая (малая) мощность;
– М ср — средняя мощность;
– М б — большая мощность.
Все эти величины принимают значения на интервале (0–1). Например, одно из продукционных правил может быть сформулирован таким образом:
ЕСЛИ Дистанция = средняя И Угол = малый, ТО Мощность = средняя.
Это правило можно представить в виде логической формулы М ср = D срj 0 = min [Dср ,j 0 ]. После формулировки всех правил получится нечеткое значение выходной переменной со степенями принадлежности ее термов. В нашем примере — это М 0 , М ср , М б .
Чтобы исполнительное устройство крана сработало, надо перейти к значению выходного с игнала системы. Это — мощность крана m. В этом заключается сущность деффазификации.
Этап 3. Дефаззификация. Наиболее распространены 3 способа дефаззификации:
– центр максимума — это, когда выходная величина становится средним значением величин m 0 , m ср , m б . Тогда m = (m 0 + m ср + m б ) / 3;
– наибольшее значение (MoM) — выбирается наибольшее значение величины: m = MAX(m 0 , m ср , m б );
– способ центроида (CoA) — здесь значение выходного сигнала системы представляет координату центра тяжести площади фигуры через усечение характеристических функций по степеням принадлежности.
Теперь есть все условия для составления алгоритма функционирования интеллектуальной системы управления в виде башенного крана:
Этап 1. На этапе фаззификации составим функции принадлежности для 3 переменных (рисунок 11).
Этап 2. Сформулируем продукционные правила. Перечислим комбинации входных переменных:
– D 0 j 0 , D 0 j ср , D 0 j б , D ср j б ; — М 0 ;
– D ср j 0, D ср j ср , D б j б ; — М ср ;
– D б j 0, D б j ср ; — М б .
Эти комбинации разобьем на 3 группы. Группы соответствуют 3 термам выходного сигнала. На основании такого разбиения напишем выражения, соответствующие продукционным правилам определения выходного сигнала:
– М 0 = D 0 И D ср j б = max [D 0; min(D ср j б )] ;
– М ср = D ср j ср И D б j б = max [min(D ср j ср ) ; min(D б j б ) ];
– М б = D б (j 0 И j б ) = min [D б ; max(j 0 j ср ) ].
Производим вычисления для: d = 25м и j = 4°. Результаты заносим в таблицу 1.
Таблица 1
Результаты вычислений по формулам (6)
|
j 0 |
j ср |
j б |
D 0 |
D ср |
D б |
М 0 |
М ср |
М б |
|
0.4 |
0.6 |
0 |
0.3 |
0.7 |
0 |
0.3 |
0.6 |
0 |
– М 0 = max [0.3 ; min(0.7;0)] = 0.3 ;
– М ср = max [min(0.7;0.6) ; min(0; 0) ] = 0.6 ;
– М б = min [0; max(0.4; 0.6) ]= 0 .
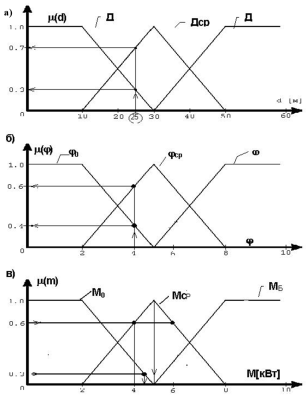
Рис. 11. Функции принадлежности входных величин (а, б) и выходного сигнала (в) системы управления башенным краном
Этап 3. Определим значения расчетов на этапе дефаззификации (рисунок 11):
– по CoM получим m = 4.5 квт;
– по MoM и CoA получим m = 5 квт.
Таким образом, для значений входных переменных d и j на двигатель следует подавать среднюю мощность, потому что величина степени принадлежности этого терма преобладает над другими.
В 2000 годы после бурного развития нечетких и интеллектуальных систем, особенно в Японии, многие технические специалисты штатов Америки и стран Европы явно заметили появления новой технологии в образе эксплуатации нечетких систем. Но к началу нового тысячелетия время было упущено. Мировым передовиком по нечетким системам стала Япония.
К концу 80-х годов в этой стране был налажен выпуск специальных нечетких контроллеров, разработанных по технологии СБИС (сейчас эта технология именуется как ПЛИС). Догонять реализацию японской технологии значило потерять десятки годы времени.
Американская фирма Intel принял альтернативное решение. В то время разнообразные промышленные контроллеры от MCS-51 до MCS-96 успешно применялись во многих цифровых платформах. Компания Intel решила предоставить разработчикам средство разработки приложений на базе этих контроллеров и включили туда возможность использования технологии по применению и внедрению нечетких систем (интеллектуализация контроллер.
Создание подобной системы позволили бы не осуществлять финансовые затраты на создание американских нечетких контроллеров. Такая созданная система получила название fuzzyTECH. В итоге такая нечеткая система была интеллектуализирована и завоевала огромную популярность в развитых странах: США, страны Европы, Япония).
Сейчас имеется многочисленные версии fuzzyTECH. Все они различаются по своим возможностям и стоимости. Приведем самый простой вычислитель из семейства fuzzyTECH — это пакет fuzzyTECH Explorer Edition.
Эта программная среда является одним из лучших средств обучения работе нечеткой системы. Она предоставляет пользователю широкие возможности по практическому освоению нечеткой технологии. Например, профессиональный пакет fuzzyTECH MCU-96 ориентирован на применение микроконтроллеров Intel семейства MCS-96.
Также имеется другой On-line вариант fuzzyTECH Edition. Эта программа может отладить реальную нечеткую систему, отлавливая ошибки прямо на ходу протекания процесса в системе. Приложение работает в реальном масштабе времени. Поэтому этот пакет незаменимое средство отладки созданных цифровых систем управления.
В составе программы fuzzyTECH аккумулированы многие алгоритмы и процедуры имеющейся нечеткой технологии: арбитражные функции принадлежности, современные методы дефаззификации и т. д.
Таким образом, среда FuzzyTECH — это полностью графическое средство поддержки разработки цифровых приложений и платформ на основе нечеткой логики. Оно является инструментом нечеткого моделирования и оптимизации реально созданного проекта. Пакет совместим с обычными средствами программной разработки. Графическое представление на экране всех этапов разработки поможет найти множество путей оптимизации или совершенствования проекта.
Пакет можно называть и генератором кода, который сможет поддерживать множество современного цифрового оборудования. Созданный пакетом fuzzyTECH исполнительный программный код можно конвертировать на язык программирования C.
Но ассемблерный код весьма уникален, наиболее корректно выполняется схемами аппаратной части и типу используемого микроконтроллера.
Покажем 5 стадии создания нечеткой системы используя программой fuzzyTECH:
- Формулировка постановки задач в виде назначения лингвистических переменных, сопоставление терма к конкретной физической величине.
- Формулирование сводов правил на основе стратегии управления системой (дефаззификация выходных данных).
- Оптимизация структуры исследуемой (анализ свойств и поведения нечеткой системы через подготовленные данные или тестирование программной модели системы).
- Организация процедуры проведения оптимизации параметров прямо в среде Интернет (тестирование структуры системы к реальному объекту и оптимизация структуры системы в реальных условиях).
- Реализация нечеткой системы (выбор варианта генерируемого кода для конкретного микропроцессора может, такой вариант может быть записан в ПЗУ реальной системы управления).
В пакете fuzzyTECH все этапы разработки осуществляются через нажатие соответствующих кнопок мыши. Внутренний код fuzzyTECH создан на языке FTL (Fuzzy Technology Language). Это аппаратно независимый объектно-ориентированный язык для разработки нечетких систем. Он имеет открытую архитектуру и может быть расширен в зависимости от потребностей пользователя.
Перечислим состав пакета программы fuzzyTECH: редакторы (Editors), отладочный модуль (Debugger), анализ созданной структуры (Analyzer), специальный генератор кодов (Code Generation — реализация нечетких систем), опции (Options — конфигуратор с инструментальным интерфейсом).
При запуске программы fuzzyTECH появляется два окна (рисунок 12): Окно Редактора проекта и Окно лингвистических переменных (LV). Редактор Проекта содержит структуру системы нечеткой логики (интерфейсы и блоки правил), LV-окно содержит список всех лингвистических переменных.
Рис. 12. Окна программы fuzzyTECH
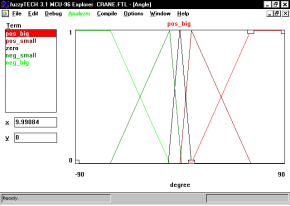
Рис. 13. Вид окна fuzzyTECH-редактирования термов
В теории нечетких множеств наиболее часто используется 3 или 7 количество термов. Обычно 1 или 2 терма не используются. Причина этого явления ясна. Человеческий разум чаще всего оценивает и представляет реальные числа (т. е. число имитации лингвистических переменных). Чаще всего в человеческом уме удобно раскладывается 3 величины: две величины низкий и высокий переделы, а также середина. Это число как терм наиболее удобно запоминается мозгом человека. Точно также можно комментировать самое большое количество термов как арабское число 7. Этот факт можно пояснить тем, что запоминание чисел включает краткосрочную память мозга. Человеческий мозг наиболее лучше работает не более 7 символическими величинами. Также известно, что переменные с «центром» или крайними «нулями» наилучше работают с нечетным количеством термов (рисунок 13).
Авторы статьи считают, что пакет программ fuzzyTECH является удачной и востребованной разработкой для углубления в теорию Искусственного интеллекта. Методика этой программы сотни раз может облегчить проектирование и создание микропроцессорных систем управления. Мы уверены, что цифровые системы в будущем поколении будут функционировать на основе теории нечеткой технологии.
Литература:
- Микропроцессорные системы автоматического управления / Бесекерский В. А. и др. — Л.: Машиностроение, Лен. отд. 1988–365с.
- Боборыкин А. В. и др. Однокристальные микроЭВМ, М.: МИКАП, 1994.
- Гребнев В. В. Однокристальные микроЭВМ (микроконтроллеры) семейства MCS-96, 1995.
- Микропроцессоры в системах автоматического управления. INTEL 8XC196MC: Учеб. пособие / Бутырин Н. Г. и др.: СПбГТУ, СПб., 1995, 115с.
- Изерман Р. Цифровые системы управления: пер. с англ. — М.: Мир, 1984–541с.
- Микропроцессорное управление электроприводами станков с ЧПУ. / Тихомиров Э. Л. и др. — М.: Машиностроение, 1990.
- Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений., М.: Мир, 1976, 165с.
- Прикладные нечеткие системы / Тэрано Т., Асаи К., Сугено М., 1993.







