Обзор существующих подходов к расчету железобетонных балок в условиях кручения с изгибом



В статье рассматриваются принципы работы железобетонных балок в условиях кручения с изгибом. Представлен обзор существующих подходов к расчету данного напряженно-деформированного состояния конструкции. Особое внимание уделено подходам, представленным в нормативной документации разных стран.

Ключевые слова: кручение с изгибом, нормативная документация, расчет железобетонной балки.

В настоящее время исследования в области расчета строительных конструкций направлены преимущественно на оптимизацию существующих подходов, уменьшения материалоемкости, учет реальной работы конструкций в условиях сложных деформаций.

Одним из таких сложных напряженно-деформированных состояний является кручение с изгибом. Пространственная работа конструкций усложняет возможность точного аналитического расчета.

Наиболее часто кручению с изгибом подвергаются железобетонные балки. Зачастую крутящие моменты, возникающие в данных конструкциях, не учитываются в расчетах, поскольку возникающее кручение либо имеет небольшую величину, либо возникло в результате случайных эксцентриситетов, либо возникающие в балках усилия могут быть перераспределены на смежные конструкции. При расчетах данных элементов кручение рассматривают как вторичный фактор, который будет учтен коэффициентами запаса или будет воспринят поперечным армированием, которое было подобрано из условия восприятия поперечных сил.

Важно понимать, как работает балка в условиях кручения с изгибом, чтобы отличать ситуации, в которых кручением пренебрегать нельзя (краевые балки, балки с боковыми консолями).

Работа в области исследования кручения с изгибом ведется с начала прошлого столетия, ей занимались такие ученые, как Е. Мерш, Г. Коуэн, Э. Г. Ц. Бах и др. В нашей стране значительный вклад в развитие теорий расчета данного напряженно-деформированного состояния внесли А. А. Гвоздев и Н. Н. Лессиг. А. А. Гвоздев [1] разработал теорию предельного равновесия, на основании которой впоследствии Н. Н. Лессиг [2] были проведены экспериментальные исследования и выведены методы расчета прочности балок, работающих в условиях кручения с изгибом.

Разрушение балки происходит по пространственному сечению, что усложняет аналитический расчет. Механизм образования трещины представлен на рис.1. А. С. Залесовом [3] был предпринят подход с заменой пространственного сечения плоским диагональным, однако, данное упрощение не всегда находит подтверждение в экспериментальных исследованиях.

Рис. 1. Пространственная трещина в балке [8, с. 57]

Нормативная документация является базой для расчета строительных конструкций. Все сооружения, возводящиеся в любой стране, должны отвечать местным требованиям норм, рассчитываться по формулам, подходам, которые представлены в них. Рассмотрим, как в нормативной документации разных стран учитывается работа конструкций в условиях кручения с изгибом.

В СП 63.13330.2018 [4] учитывается работа конструкции в условиях кручения с изгибом по некоторому обобщенному закону. Расчет по прочности пространственных сечений с использованием кривых взаимодействий крутящих и изгибающих моментов производится по формуле (1):

(1)

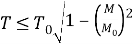
где — крутящий момент от внешней нагрузки в пространственном сечении;

— предельный крутящий момент, воспринимаемый пространственным сечением;

— изгибающий момент от внешней нагрузки в нормальном сечении;

— предельный изгибающий момент, воспринимаемый нормальным сечением.

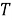
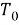
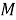
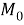
Формула расчета (1) может быть представлена в виде:

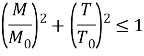
Или в виде кривой зависимости (Рис. 2).

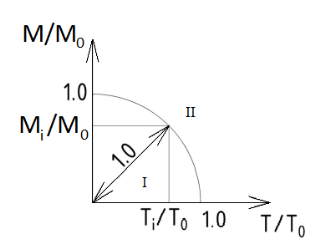
Рис. 2. Кривая взаимодействия для элемента, работающего на кручение с изгибом. I — область обеспеченной прочности; II — область необеспеченной прочности

Если точка с координатами лежит в пределах области, ограниченной кривой и осями координат, то прочность сечения обеспечена, если за пределами данной области — прочность обеспечена не будет.

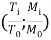
В основе подхода расчета по СП лежит принцип, по которому несущая способность балки на кручение уменьшается на величину, необходимую для восприятия изгибающего момента.

В индийских строительных нормах IS 456:2000 [7] также представлены формулы, которые учитывают связь двух силовых факторов. Продольное армирование подбирается из условия действия фиктивного изгибающего момента, который является функцией действующих в конструкции изгибающего и крутящего моментов.

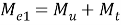
где — изгибающий момент в поперечном сечении

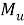
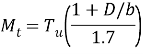
где — это крутящий момент;

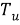
D — полная высота сечения балки;

b — это ширина балки.

В американских ACI 318–14 Building Code [5] и европейских строительных нормах EN 1992–1–1 [6] подбор армирования для восприятия изгибающего и крутящего моментов производится независимо друг от друга, сначала подбирается армирование для восприятия изгибных усилий, затем подбирается арматура для восприятия кручения (поперечная и продольная). Затем продольная арматура для восприятия всех силовых факторов суммируется. Данный подход приводит к большим запасам прочности, что подтверждается экспериментальными исследованиями.

Литература:

1. Гвоздев, А. А. Расчет несущей способности по методу предельного равновесия / А. А. Гвоздев. — М.: Стройиздат, 1949. — 279 с.

2. Лессиг, Н. Н. Определение несущей способности железобетонных элементов прямоугольного сечения, работающих на изгиб с кручением. / Н. Н. Лессиг / Исследование прочности элементов железобетонных конструкций: сб. трудов НИИЖБ. — М.: НИИЖБ, 1959. — № 5.

3. Залесов, А. С. Расчет железобетонных конструкций по прочности, трещиностойкости и деформациям. / Залесов А. С., Кодыш Э. Н., Лемыш Л. Л., Никитин И. К. — М. Стройиздат., 1988 г. — 120 с.

4. СП 63.13330.2018. Бетонные и железобетонные конструкции. Основные положения. / Госстрой России. -М.: ГУП НИИЖБ, 2012.-155 с.

5. ACI 318–14 Building Code Requirements for Structural Concrete and Commentary, American Concrete Institute, 2014–524 с.

6. EN 1992–1–1:2004 Eurocode 2: Design of concrete structures — Part 1–1: General rules and rules for buildings — Brussels, 2004–227 с.

7. IS 456 (2000): Plain and Reinforced Concrete — Code of Practice (Fourth Revision) — New Delhi, 2000–114 с.

8. Elfgren, L. Reinforced Concrete Beams Loaded in Combined Torsion, Bending and Shear. A study of the ultimate load-carrying capacity / L. Elfgren. — Göteborg: Division of Concrete Structures, 1972–233 с.