В данной статье приводится рекурсивный алгоритм решения судоку (с помощью «грубой силы»). Приводится способ проверки найденного решения на единственность с помощью модификации того же алгоритма. Доказывается, что этот способ работает для любого судоку.
Ключевые слова: судоку, решение судоку, рекурсия, рекурсивный алгоритм, единственность решения судоку.
Судоку — это незамысловатая головоломка, главной целью которой является заполнение квадрата 9 х 9 ячеек числами от 1 до 9 по специальным правилам. Решение судоку — вид досуга, однако существуют соревнования по его скоростному решению.
Написание программы для автоматического решения судоку является упражнением для программиста, изучающего алгоритмы. В настоящее время существует множество онлайн сервисов, позволяющих подобрать решение для классического судоку [1], [2]. Также, можно найти примеры программ на разных языках программирования, решающие судоку и использующие как «человеческие» методы решения судоку [3], так и алгоритм Х (алгоритм Кнута) для поиска точного покрытия множества [4].
В приведенных выше примерах не учитывается проверка «правильность» поставленной задачи. Напомним, что правильным (валидным) судоку является судоку с такими входными данными, которое имеет одно единственное решение [5].
В данной статье будет рассмотрен алгоритм решения судоку с помощью «грубой силы», т. е. решение полным перебором возможных вариантов решения задачи и показан способ проверки полученного решения на единственность.
Идея алгоритма
Напомним правила классического судоку [5]:
- Поле головоломки представляет собой квадрат, состоящий из 81 клетки;
- Часть клеток изначально заполнены числами от 1 до 9 (подсказки);
- В каждом ряду и столбце любое число от 1 до 9 может встречаться лишь один раз;
- Кроме того, все поле делится еще на 9 блоков 3x3, в которых цифры от 1 до 9 тоже могут встречаться лишь один раз;
- Задача заключается в том, чтобы заполнить все клетки цифрами с учетом указанных ограничений.
Нельзя забывать:
- Валидное судоку должно иметь одно и только одно решение.
Блок-схема рекурсивного решения судоку без проверки на валидность представлена на рисунке 1. Рекурсивный вызов происходит внутри цикла (овальный блок «решатель судоку»), который вызывает саму эту функцию.
Необходимо понимать, что во время работы этого алгоритма информация о поле головоломки присутствует где-либо в программе (в глобальной переменной или всегда передаётся внутрь по указателю и пр.). Шаги по чтению/записи в это структуру данных в данной блок-схеме опущены, т. к. в общем случае они могут быть разными, и они ухудшают восприятие блок-схемы.
Блок условия «Входные данные валидны?» представляет собой проверку, только на то, что в каждом строке/стобце/блоке числа не повторяются. Обратите внимание, что в данном алгоритме не используются разнообразные методы решения судоку «последний герой», «выбора нет» и прочие [6].
Блок условия «Есть свободная клетка?» проверяет, существует ли на поле свободная клетка, если да, то следующее число мы будем записывать в неё.
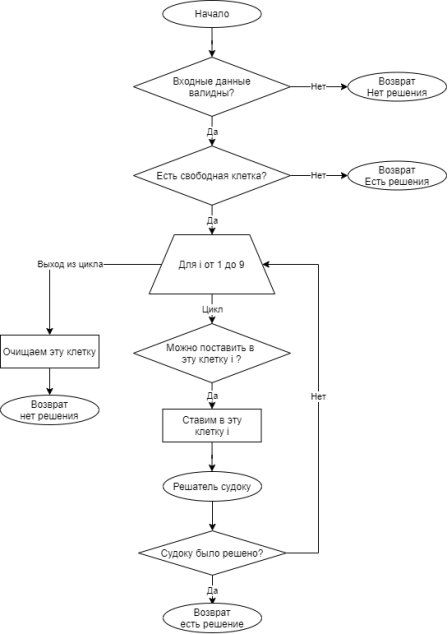
Рис. 1. Блок-схема рекурсивного решения судоку
Проверка решения на единственность
Возьмем поле для судоку, которое гарантированно будет иметь больше одного решения (рисунок 2 слева). Рекурсивный алгоритм будет по очереди заполнять клетки этого поля, пока в конце концов не найдет подходящее решение (рисунок 2 справа).
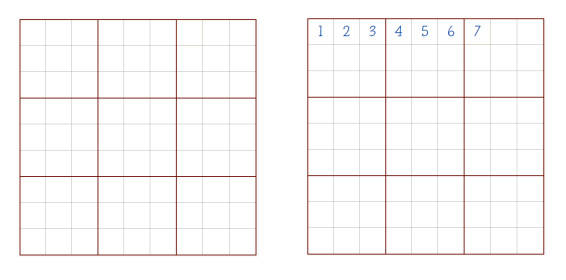
Рис. 2. Судоку с несколькими решениями (слева), процесс работы рекурсивного алгоритма (справа)
Идея проверки на единственность решения заключается в том, чтобы запустить заполнение поля судоку числами не от 1 до 9, а от 9 до 1. Если после обоих заполнений решения оказались разными, то судоку имеет несколько решений, т. е. исходная задача не валидна. Если решения совпали, то судоку валидно, т. е. имеет ровно одно решение. На рисунке 3 представлено заполнение пустого поля от 1 до 9 и от 9 до 1, наглядная демонстрация, что данное судоку имеет несколько решений.
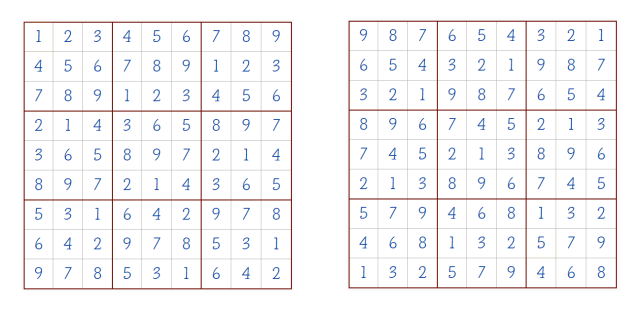
Рис. 3. «Пустое» судоку заполняется от 1 до 9(слева) и от 9 до 1 (справа)
Доказательство
Поле судоку будем представлять в вдие 81-значного числа. Причем старшинство разрядов должно соответствовать обходу алгоритмом клеток поля судоку. Каждое такое число будем называть полем судоку.
Например, полю на рисунке 3 слева будет соответствовать число
1234567894567891237…8531978531642.
Представим теперь последовательность чисел от 0 до 10^81–1. Числа меньшие 10^80 будем дополнять для удобства незначащими лидирующими нулями:
0000000000…0000000000
0000000000…0000000001
0000000000…0000000002
…
1000000000…0000000000
1000000000…0000000001
…
9999999999…9999999998
9999999999…9999999999
Удалив из этой последовательности все невалидные поля судоку мы получим множество всех возможных решенных судоку.
Наложим на это множество «маску» из нашего изначального поля (пустые клетки — любое число, заполненная клетка должна точно совпасть с соответствующей позицией числа из полученного выше множества). Удалив все поля, несоответствующие маске мы получим множество всех возможных решений нашего судоку. Причем поля (числа) в этом множестве будут отсортированы по возрастанию.
Производя полный перебор путём подстановки в свободные клетки чисел от 1 до 9 мы «продвигаемся» по этой последовательности от меньших чисел к большим. А подставляя числа от 9 до 1 мы «продвигаемся» от больших к меньшим.
Если в множестве возможных решений больше одного элемента, то алгоритм найдет разные ответы: самое «большое» поле-число и самое «маленькое» поле-число. Если в множестве ровно 1 элемент (единственное решение судоку), то эти ответы совпадут.
Примечание по эффективности полного перебора
На первый взгляд может показаться, что рекурсивный полный перебор поиска решения судоку должен занимать очень большое время (10^81 операций, например). Однако, для написанной программы автору не удалось найти примера судоку, который решался бы программой дольше, чем за 1 секунду.
Если убрать проверку судоку на валидность перед запуском основного алгоритма, и попробовать, например, решить судоку, где в первых двух клетках находятся «1», а остальные клетки пустые (очевидно, невалидные входные данные), то действительно, программе требуется значительное время, чтобы понять, что ответа не существует (автор ни разу этого не дождался).
Заключение
Как говорилось ранее, написание программы для решения судоку является упражнением для программиста. Однако, проверка решения на единственность не так очевидна.
Следующим по сложности упражнением может стать проверка единственности решения судоку для более эффективного алгоритма — алгоритма X.
Литература:
- Решатель судоку. — Программа: веб-сервис — URL: https://sudokus.ru/reshateli/ (дата обращения 10.12.2020)
- Sudoku solver. — Программа: веб-сервис — URL: https://sudokuonline.ru/resatel-sudoku-onlajn/ (дата обращения 10.12.2020)
- Решаем судоку на JavaScript. — Текст: электронный // Хабр. — URL: https://habr.com/ru/post/113837/ (дата обращения 10.12.2020)
- Решаем судоку с помощью Алгоритма X. — Текст: электронный // Хабр. — URL: https://habr.com/ru/post/462411/ (дата обращения 11.12.2020)
- Судоку. — Текст: электронный // Википедия свободная энциклопедия. — URL: https://ru.wikipedia.org/wiki/Судоку (дата обращения 10.12.2020)
- Методы решения судоку. — Текст: электронный // Хабр. — URL: https://habr.com/ru/post/173795/ (дата обращения 11.12.2020)







