Задачи Дарбу и Коши для линейных гиперболических уравнений с постоянными коэффициентами



Многие явления механики, физики, биологии сводятся к исследованию гиперболических уравнений. Чтобы эти явления описать полностью для гиперболических уравнений, ставится задача Дарбу и для дальнейших изучений необходимо явное представление рассматриваемой задачи.

В данной статье изучаются задачи Дарбу и Коши для линейных гиперболических уравнений с постоянными коэффициентами.

Показано, что эта задача имеет единственное решение и получен ее явный вид.

Ключевые слова : уравнение Вольтерра, функция Римана, функция Бесселя, задача Коши.

Many phenomena of mechanics, physics, and biology are reduced to the study of hyperbolic equations. In order to describe these phenomena completely, the Darboux problem is posed for hyperbolic equations, and for further studies, an explicit representation of the problem under consideration is necessary.

In this article discusses, we study the Darboux and Koshi problems for linear hyperbolic equations with constant coefficients.

It is shown that this problem has a unique solution and its explicit form is obtained.

Keywords: Volterra equation, Riemann function, Bessel function, Cauchy problem.

Введение

Математические модели многих задач газовой динамики, аэродинамики и ряда других моделей процессов механики, физики, биологии сводятся к исследованию гиперболических уравнений ([1–4]).

Задача Дарбу вместо с задачей Коши являются основными задачами для двумерных гиперболических уравнений. Теория этих задач, в силу их прикладной и теоретической важности стала одним из центральных разделов современной теории уравнений с частными производными ([3–5]).

В данной работе изучаются задачи Дарбу и Коши для линейных гиперболических уравнений с постоянными коэффициентами.

Показано, что эта однозначна разрешима и получен явный вид его решения.

Постановка задачи

Пусть - конечная область, ограниченная отрезком оси , при прямыми и

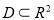
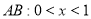
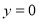
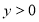
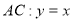
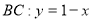
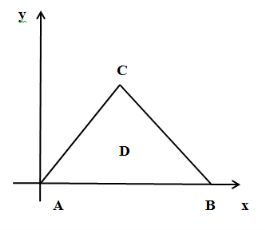
Рис. 1

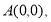
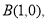
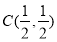
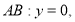
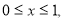
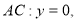
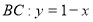
В области рассмотрим линейные гиперболические уравнения с постоянными коэффициентами

(1)

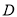
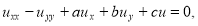
где

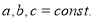
Задача Коши:

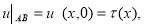
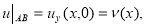
Первая задача Дарбу:

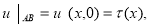
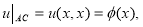
Вторая задача Дарбу:

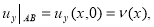
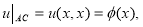
Первая сопряженная задача Дарбу:

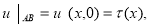
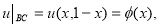
Вторая сопряженная задача Дарбу:

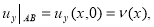
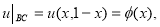
В качестве сопряженной второй задачи Дарбу для уравнения (1) рассмотрим следующую задачу

Задача 2*. Найти решение уравнения (1) в области из класса удовлетворяющее краевым условиям

(2)

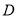
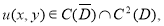
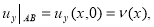
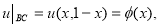
где

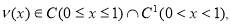
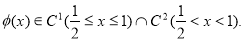
Имеет место.

Теорема. Задача 2* имеет единственное решение.

Доказательство. Введем новую неизвестную функцию по формуле

(3)

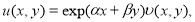
где - пока неизвестные параметры.

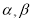
Подставляя функцию (3) в уравнение (1) и краевое условие будет иметь

. (4)

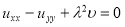
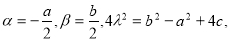
при этом из (2) получим

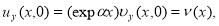
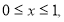
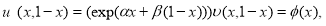
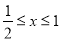
или

(5)

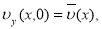
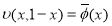
где

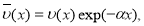
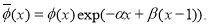
Таким образом, вместо задачи (1),(2) пришли к задаче (4),(5) в области

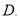
В характеристических координатах

задача (4),(5) записывается в следующем виде

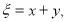
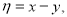
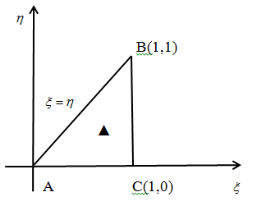
Рис. 2

Область

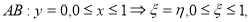
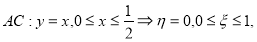
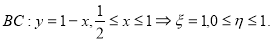
переходит в область .

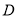
Задача 2’ . Найти в области ∆ решение уравнения

(6)

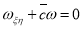
из класса удовлетворяющее краевым условиям

(7)

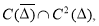
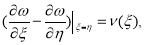
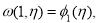
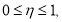
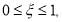
где

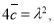
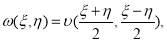
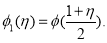
Так как в (6) , то из решения задачи Коши ([3–5]) для уравнения (6) получим следующую формулу

(8)

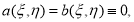
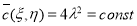
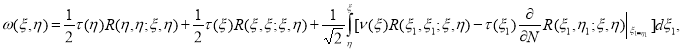
где - функция Римана уравнения (6).

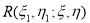
Известно ([6]), что эта функция представимо в явном виде

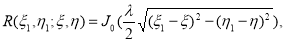
где -функция Бесселя первого рода нулевого порядка [7]

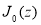
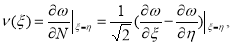
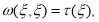
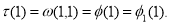
Из (8) при будем иметь

(9)

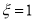
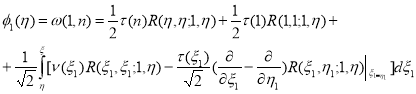
Проведя некоторые вычисления относительно из (9), а также из ([7]) получим интегральное уравнение Вольтерра второго рода относительно

(10)

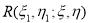
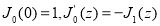
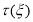
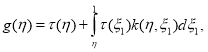
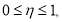
Которое имеет единственное решение ([8]) и она выписывается в явном виде.

Здесь

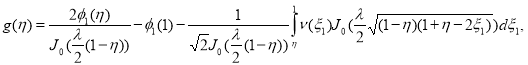
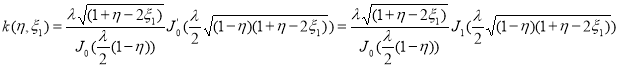
Таким образом задача (6),(7)(т. е. задача 2’) имеет единственное решение вида (8), где

определяется из интегрального уравнения (10).

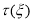
Отсюда следует и задача 2* имеет решение вида

и можно записать ее в явном виде, где находится из (8).

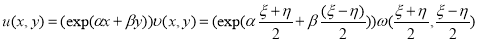
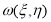
Теперь покажем, что решение задачи 2* (т. е. задача 2’) единственно. Пусть — два решения задачи 2* с данными (2). Тогда функция удовлетворяет уравнению (1) с однородными данными

(11)

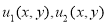
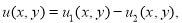
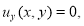
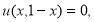
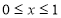
Тогда из задачи (1),(11) приходим к задаче для уравнения (6) с условием

(12)

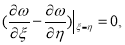
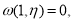
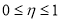
Далее из решения задачи Коши (8), с учетом (12) будем иметь

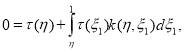
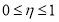
которое имеет тривиальное решение ([8]) т. е.

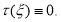
Значит, из (8) получим т. е.

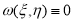
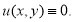
Следовательно,

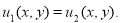
Единственностьзадачи 2* показана.

Теорема доказана.

Литература:

1. Тихонов А. Н., Самарский А. А. Уравнения математической физики, М.: Наука, 19722–724 с.
2. Бицадзе А. В. Уравнения математической физики, М.: Наука, 1976–336 с.
3. Бицадзе А. В. Некоторые классы уравнений в частных производных, М.Наука, 1981–448 с.
4. Нахушев А. М. Уравнения математической биологии, М.: Высшая школа, 1995–301 с.
5. Алдашев С. А. Краевые задачи для многомерных гиперболических и сммешанных уравнений, Алматы: Гылым, 1994–170 с.
6. Курант Р. Уравнения с частными производными, М.: Мир.1964–830 с.
7. Бейтмен Г., Эрдейн А. Высшие трансцендентные функции, т.2, М.: Наука, 1974–295 с.
8. Смирнов В. И. Курс высшей математики, т.4, ч.2, М.: Наука, 1974–334 с.