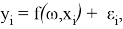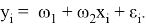Рассмотрено использование языка R для анализа данных, в частности, при анализе данных всемирного рейтинга университетов. Разработана и протестирована модель прогнозирования места университета в рассматриваемом рейтинге.
Ключевые слова: язык R, регрессионный анализ, всемирный рейтинг университетов.
The use of the R language for data analysis when analyzing data from the world ranking of universities, is considered. A model for predicting a place in the ranking of universities has been developed and tested.
Key words: R language, regression analysis, world university ranking.
На сегодняшний день существует множество международных рейтингов университетов. Списки рейтингов университетов полезны тем, кто выбирает, в какой стране учиться или планирует получить работу за рубежом (особенно в области исследований, преподавания, бизнеса). Одним из них является рейтинг Times Higher Education (THE), который предоставляет достоверные данные об университетах для студентов, преподавателей, руководителей университетов, правительств и промышленности с 2004 г. [1]. Составители рейтинга Times Higher Education исследовали вузы из 79 стран и выбрали лучшие университеты мира по качеству преподавания и исследовательской деятельности, уровню распространения знаний и инноваций. Также эффективность вузов и качество их материальной базы оценивается THE на основе финансовых показателей.
Для анализа факторов, на которые необходимо обратить внимание руководству университета, была создана модель на языке R, с возможностью прогноза рейтинга университета, на основе имеющихся факторов. Данная модель позволяет предсказать возможность попадания университета в рейтинг или возможность увеличения своей позиции в рейтинге.
Язык R — язык программирования для статистической обработки данных и работы с графикой, а также свободная программная среда вычислений с открытым исходным кодом в рамках проекта GNU. R широко используется как статистическое программное обеспечение для анализа данных и фактически стал стандартом для статистических программ [2].
Входные данные для анализа формируются в виде файла формата csv, содержащего набор показателей для каждого университета, представленного в рейтинге. Данные для анализа взяты с сайта kaggle.com [3]. Файл с входными данными содержит 1603 строки и 10 показателей (рис. 1).
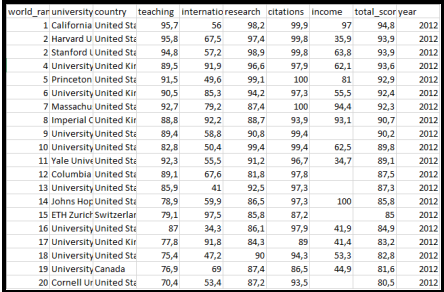
Рис. 1. Формат входных данных
Входными переменными csv файла, содержащего рейтинг университетов по версии THE, являются:
1 — World_rank (Ранг университета в мире, текст)
2 — University_Name (Название университета, текст)
3 — Country (Страна, в которой находится университет, текст)
4 — Teaching (Рейтинг преподавания в университете, число)
5 — International (Рейтинг иностранных студентов, число)
6 — Research (Рейтинг исследований университета, число)
7 –Сitations (Рейтинг цитируемости работ университета, число)
8 — Income (Рейтинг знаний выпускников, число)
9 — Total_score (Общий балл, используемый для составления рейтинга, число)
10 — Year (Год анализа рейтинга, число)
Статистический анализ данного файла показывает, что основную информацию о выборке можно получить, используя функцию “summary” языка R. Эта функция сообщает минимальное и максимальное значения, медиану, среднее, первый, и третий квартиль задаваемого параметра (табл. 1).
Таблица 1
Статистический анализ файла
|
Столбец |
Min. |
1 st Qu. |
Median |
Mean |
3 rd Qu. |
Max |
NA’s |
|
Teaching |
10.70 |
26.25 |
34.90 |
38.79 |
46.80 |
96.30 |
- |
|
International |
12.70 |
35.75 |
53.00 |
53.49 |
69.40 |
98.90 |
- |
|
Research |
6.50 |
21.90 |
32.10 |
37.35 |
47.40 |
99.40 |
- |
|
Сitations |
3.10 |
50.20 |
64.20 |
64.39 |
79.60 |
100.00 |
- |
|
Income |
24.20 |
34.10 |
41.90 |
49.81 |
60.40 |
100.00 |
122 |
|
Total_score |
41.40 |
49.20 |
54.60 |
59.03 |
65.60 |
95.50 |
802 |
|
Year |
2012 |
2012 |
2013 |
2013 |
2014 |
2015 |
- |
Ниже приведен пример программы, которая строит модель зависимости по заданной выборке и показывает результат на графике. Для заданного множества из m пар (x i , y i ), i=1, …, m, значений свободной и зависимой переменной требуется построить зависимость. Эта зависимость представлена в виде линейной регрессии:
|
|
(1) |
где
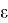
x, y — переменные (принимают значения на числовой прямой R).
Предполагается, что случайная величина распределена нормально с нулевым мат. ожиданием и фиксированной дисперсией
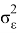
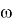
Одномерная регрессия определяется как:
|
|
(2) |
Основываясь на этом, построим модель, которая позволяла бы предсказывать рейтинг университета на основе его показателей. Результат программы представлен на рис. 2.
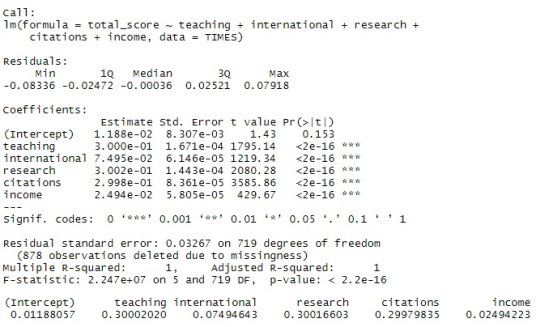
Рис. 2. Множественная регрессия и коэффициенты регрессии
Из результата работы программы видно, что коэффициент детерминации R-squared равен 1. Данный показатель указывает на то, что связь между факторами регрессии и зависимой переменной является очень тесной. Значение скорректированного коэффициента детерминации Adjusted R-squared равно 1, значит зависимость является ярко выраженной. Значение параметра F-statistic, равное 2.247е +07 , говорит о высокой значимости модели. Если критерий t-value, больше 2, то фактор является значимым для модели. Соответственно, для рассматриваемой модели все факторы являются значимыми.
Вероятность истинности нуль гипотезы p-value, которая гласит, что независимые переменные не объясняют динамику зависимой переменной, и, при p-value равным 2.2e -16 нуль гипотеза является ложной, что говорит о том, что связь между факторами регрессии и зависимой переменной существует.
Создадим новый датафрейм с новыми значениями университетов, повторяющими реальный университет из рейтинга (рис. 3). После чего предскажем значение рейтинга университета по предлагаемой модели, а также проверим ее адекватность.

Рис. 3. Датафрейм с новыми значениями
В результате работы программы прогнозирования рейтинга университетов получено значение рейтинга университета — 49.98265. Сравнив результат с реальным университетом в рейтинге, данные которого совпадают с заданными (табл. 2), видим, что реальный рейтинг университета 50.0, Отклонение составляет 0.01735.
Таблица 2
Реальные данные университета в рейтинге
|
world_ rank |
university _name |
country |
teaching |
international |
research |
citations |
income |
total_ score |
year |
|
125 |
Aarhus University |
Denmark |
30.7 |
69.3 |
49.0 |
64.0 |
67.0 |
50.0 |
2012 |
Таким образом, разработанная модель позволяет предсказывать место университета во всемирном рейтинге университетов Times Higher Education, на основе имеющихся факторов. Для разработки данной модели была определена статистика показателей для данного рейтинга. Построенная модель была протестирована на работоспособность и показала хороший результат по прогнозированию рейтинга с минимальным отклонением.
Литература:
- WorldUniversityRankings [Электронный ресурс] // — Режим доступа: https://www.timeshighereducation.com/world-university-rankings (дата обращ. 21.12.2020).
- R (язык программирования) [Электронный ресурс] // — Режим доступа: https://ru.wikipedia.org/wiki/R_(язык_программирования) (дата обращ. 21.12.2020)
- WorldUniversityRankings [Электронный ресурс] // — Режим доступа: https://www.kaggle.com/mylesoneill/world-university-rankings (дата обращ. 21.12.2020).
- Линейная регрессия [Электронный ресурс] // — Режим доступа: http://www.machinelearning.ru/wiki/index.php?title=Линейная_регрессия_ %28пример %29 (дата обращ. 21.12.2020)