В статье автор рассматривает метод ветвей и границ, применяя его к решению задачи о коммивояжёре для нахождения наименьшего пути, а также проводит сравнение с методом грубого перебора.
Ключевые слова: минимальный путь, поиск пути, задача о коммивояжёре, метод ветвей и границ, грубый перебор, алгоритм
В современном мире оптимизация алгоритмов является очень важной проблемой, так как системы должны обрабатывать все большие данные за меньшее время. Одной из известных задач является задача коммивояжёра. Цели данной статьи — оптимизировать решение задачи о коммивояжёре с помощью метода ветвей и границ, разработать алгоритм решения для задачи на языке С++, оценить количество переборов при решении задачи стратегией с помощью грубой силы и с разработанным методом.
Формулировка задачи:
Есть N городов, соединённых между собой дорогами. Необходимо проложить между ними кратчайший замкнутый маршрут, проходящий через каждый город только один раз.
Расстояние из города j в город i считается неотрицательным числом: Dji ≥ 0. Часто Dji называют стоимостью ребра, так как дороги можно представить рёбрами, соединяющими города-вершины некоторого графа.
Допускается несимметричность матрицы Dji ≠ Dji. В ещё более общем случае пути между некоторыми городами могут отсутствовать.
Исходные условия можно записать в формате таблицы, где строки — города отправления, столбцы — города прибытия, в ячейках расстояния между ними.
Необходимые поля:
− Количество узлов
− Массив минимального пути
− Посещенные пути при текущем проходе
− Вес минимального пути
Необходимые методы:
− Начальный метод поиска пути
− Рекурсивный метод построения пути для заданного начала (в качестве параметра)
− Первый минимум массива
− Второй минимум массива
− Сохранение пути
Алгоритм начального метода поиска пути
− Инициализация нижней границы (bound):
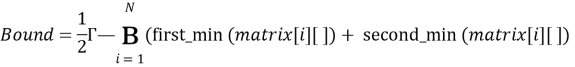
− Цикл вызова рекурсивного поиска минимального пути для каждого узла в качестве начальной точки
Алгоритм рекурсивного поиска пути
− Если все пройдено
-
Если есть путь до начальной точки
- Длина пройденного пути = переданная длина + путь до начальной точки
-
Если длина пути меньше минимальной длины
- Сохраняем путь и длину в качестве минимальных
- Завершаем метод
− Иначе проходим по всем путям (i=0..N-1)
-
Если есть путь до не посещенной точки
- Сохраняем нижнюю границу
- Идем в узел i
- Добавляем к текущей длине пути
- Вычисляем нижнюю границу для текущего пути по формуле выше
− Если текущая длина + граница для текущего пути меньше минимума
- Рекурсивный вызов следующего уровня (проходим в узел i)
- Обрезаем узел
- Очищаем массив посещенных узлов
Расчеты
В ходе тестирования метода ветвей и границ было совершено 30 генераций матриц и использован метод поиска пути для каждой из них. Результаты представлены в таблице 1. При использовании грубого метода использовалось:
(10! вариантов путей) * (10 переходов на 1 путь) = 36 288 000 переходов
Таблица 1
Таблица количества переходов
|
Номер матрицы |
Количество переходов |
Номер матрицы |
Количество переходов |
Номер матрицы |
Количество переходов |
|
1 |
89 |
11 |
476 |
21 |
442 |
|
2 |
179 |
12 |
113 |
22 |
691 |
|
3 |
2340 |
13 |
2294 |
23 |
605 |
|
4 |
689 |
14 |
1819 |
24 |
483 |
|
5 |
1616 |
15 |
3240 |
25 |
2180 |
|
6 |
309 |
16 |
290 |
26 |
147 |
|
7 |
4175 |
17 |
3270 |
27 |
1262 |
|
8 |
2365 |
18 |
2606 |
28 |
622 |
|
9 |
914 |
19 |
734 |
29 |
97 |
|
10 |
93 |
20 |
3576 |
30 |
2099 |
Среднее количество переходов: 1328 , что меньше грубого подхода в 27 325 раз.
Вывод
Исследовав метод ветвей и границ, можно сделать вывод, что данный способ в разы превосходит по количеству итераций метод грубого перебора, несмотря на свою простоту в реализации.
Литература:
1. Тема 4: Методы неявного перебора. — Текст: электронный // Дискретные задачи размещения: [сайт]. — URL: http://math.nsc.ru/LBRT/k4/or/or_part4.pdf (дата обращения: 06.01.2021).
2. Глава 4. Задача коммивояжера. — Текст: электронный // Дискретные задачи размещения: [сайт]. — URL: http://www.math.nsc.ru/LBRT/k5/OR-MMF/TSPr.pdf (дата обращения: 07.01.2021).
3. Метод ветвей и границ. — Текст: электронный // Экономико-математические методы: [сайт]. — URL: http://www.math.mrsu.ru/text/courses/method/metod_vetvei_i_granic.htm (дата обращения: 06.01.2021).







