В статье осуществляется оценка возможностей грунтово-железнодорожного транспортного средства преодолевать повороты при движении по железнодорожным путям без задевания других транспортных средств и приближающихся строений.
Ключевые слова: грунтово-железнодорожное транспортное средство, движение на повороте, отсутствия столкновений при движении на соседних путях.
Использование на железной дороге ГЖТС, отличающегося по конструкции от стандартного вагона и спроектированного без учета требований, предъявляемых к различным типам вагонов на предмет отсутствия столкновений при движении на соседних путях, вызывает необходимость определения максимальных величин выступающих частей ГЖТС.
Рассмотрим два соседние пути, имеющие закругления по известным радиусам. Обозначим расстояние между рельсами пути через «а« (а = 1524 мм), а расстояние между соседними рельсами двух смежных путей через «в« (рис.1).
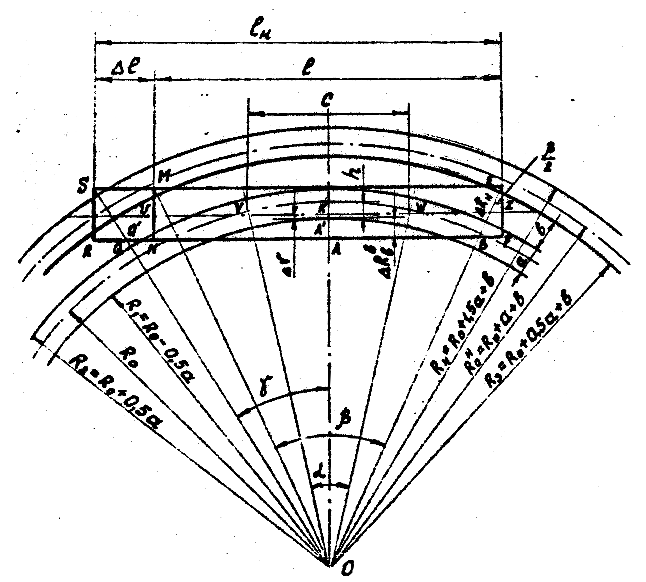
Рис. 1. Схема расположения ГЖТС на железнодорожных путях
Средний радиус закругления внутреннего пути обозначим через
R
0
. Тогда радиус закругления внутреннего рельса
R
1
= R
0–
0,5а; радиус закругления наружного рельса
R
2
= R
0
+
0,5а. Для наружного пути средний радиус закругления
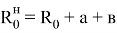
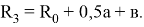
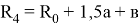
Определим наибольшую величину выступающих частей ГЖТС по отношению к внутреннему рельсу. Вначале определим эту величину для внутреннего пути —
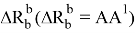
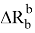
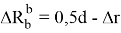
где
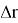
Для определения величины
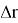
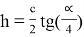
где
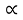
При этом
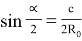
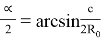
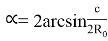
Угол
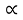
Найдем расстояние ОК
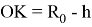
После этого определим величину
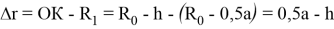
Подставив выражение (4) в зависимость (1), получим наибольшую величину выступающей части ГЖТС по отношению к внутреннему рельсу
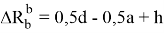
Для транспортного средства, расположенного на наружном пути, наибольшая величина выступающей части по отношению к внутреннему рельсу наружного пути
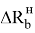
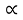

Определим наибольшую величину выступающей части транспортного средства по отношению к наружному рельсу внутреннего пути
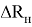
Рассмотрим треугольник ОАВ (рис. 1). Из указанного треугольника
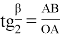
Откуда
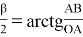
Выразим АВ и ОА через известные величины
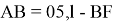
Значение BF определим из треугольника BEF, учитывая, что угол BEF равен β/2.
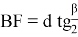
Подставив выражение (9) в формулу (8), получим
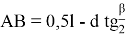
Значение ОА выразим через радиус
R
1
и
величину
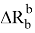
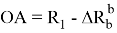
Подставив выражения (10) и (11) в зависимость (7), получим
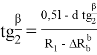
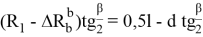
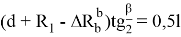
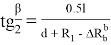
Откуда
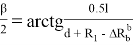
Если провести окружность радиусом
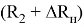
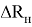
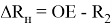
В рассматриваемом сегменте сторона МЕ = l транспортного средства определяется по зависимости
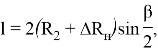
откуда
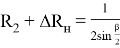
Выразив из последнего выражения
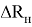
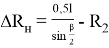
Зависимости для
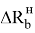
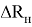
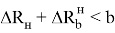
Это условие сохраняется не только для однотипных транспортных средств, но и для транспортных средств различных конструкций. При этом для вычисления значений
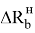
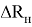
Как уже отмечалось, приведенная выше методика справедлива для случая симметричного расположения шкворня железнодорожных тележек ГЖТС по отношению к его торцам. Однако на ГЖТС шкворни могут быть расположены на разных расстояниях от торцов. Например, передний шкворень может находиться на большем расстоянии от переднего торца транспортного средства, чем задний.
Заметим, что асимметрия расположения шкворней транспортного средства по отношению к торцам не влияет на величины
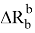
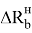
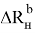
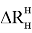
Обозначим наибольшую величину выступающей части транспортного средства по отношению к наружному рельсу в случае асимметрии расположения шкворней через
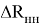
Тогда
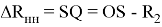
Из треугольника OTS находим
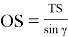
кроме того,
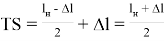
где
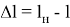
После подстановки зависимости (20) в выражение (19) получим
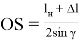
Подставив (21) в (18), найдем
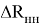
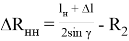
Определим угол γ через известные величины. Из треугольника OAQ 1 находим
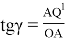
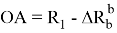
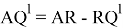
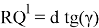
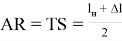
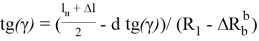
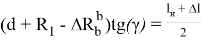
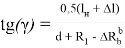
Если в зависимость (23) подставить выражения для
R
1
и
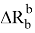
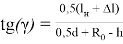
По зависимостям (23) и (24) находим выражение для угла γ
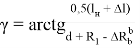
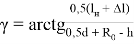
Точка Е, противоположная точке S, будет выступать на величину
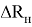
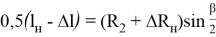
откуда
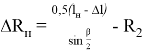
Причем угол β/2 определяется по зависимости
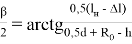
Эта зависимость получается аналогично зависимости (24) с использованием треугольника ОТЕ.
Отметим, что если шкворни ГЖТС расположены симметрично относительно его торцов, т. е.
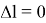
На рис. 2 представлены зависимости значений величин выступающих частей различных транспортных средств от радиуса кривизны путей.
Рассматривались ГЖТС с базами С = 8,65 м; С = 7,7 м с симметричным расположением шкворней и вагон с базой С = 17 м также с симметричным расположением шкворней. Ширина ГЖТС принималась равной 3,75 м и 3,04 м.
Кривые 1…4 получены для ГЖТС, расположенного на внутреннем пути; кривые 1 l …4 l — при нахождении на внешнем пути.
Кривая 5 l получена для вагона, расположенного на внешнем пути, а кривая 5 — при расположении вагона на внутреннем пути.
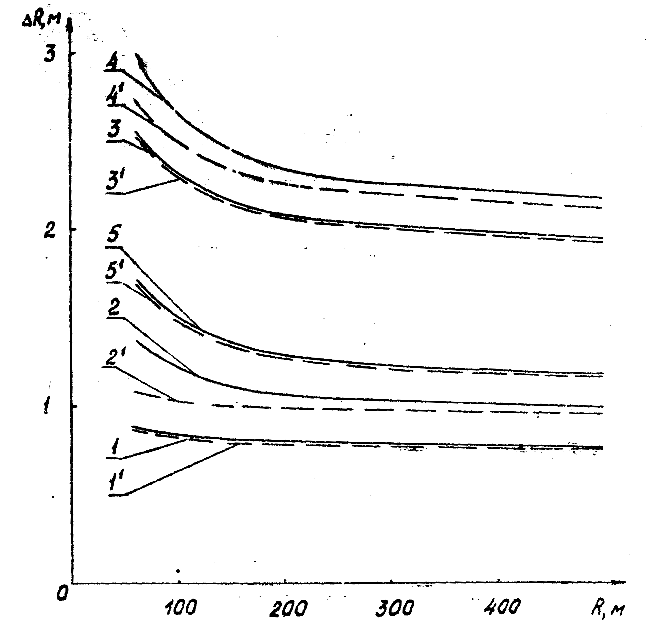
Рис. 2. Величины выступающих частей ГЖТС и вагона с симметричным расположением шкворней
При радиусах кривизны пути свыше 300 м изменение значений выступающих частей транспортных средств происходит незначительно.
На рис. 3 показаны величины выступающих частей ГЖТС и вагона с несимметричным расположением шкворней.
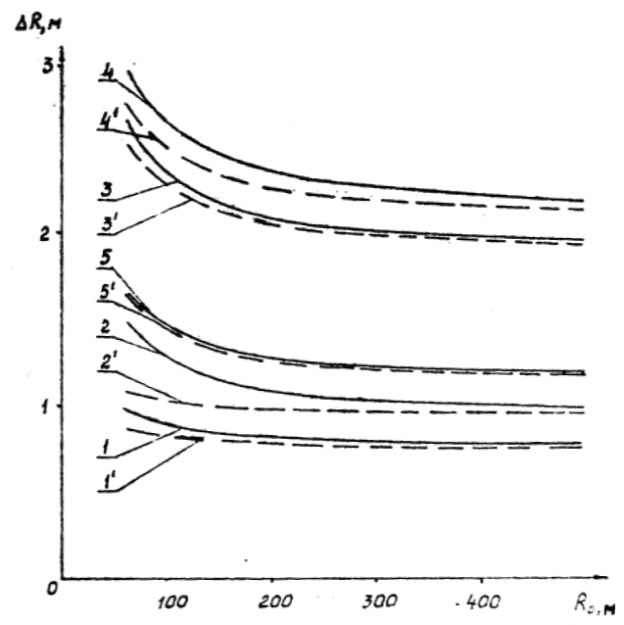
Рис. 3. Величины выступающих частей ГЖТС и вагона с несимметричным расположением шкворней
В случае несимметричного расположения шкворней на ГЖТС величины выступающих частей на повороте будут больше.
Литература:
- Антонов, А. С., Кононович Ю. А. и др. Армейские автомобили. Теория. — М.: Военное издательство МО СССР, 1970, 526 с.
- Степанченко, Э. П., Фалалеев П. П. Технологическое оборудование. — М.: МО СССР, 1986, 364 с.
- Литвинов, А. С., Фаробин Я. Е. Автомобиль: Теория эксплуатационных свойств: Учебник для вузов по специальности «Автомобили и автомобильное хозяйство». — М.: Машиностроение, 1989.—240 с.
- Вахламов, В. К. Автомобили: Эксплуатационные свойства: учебник для студ. Высш. Учеб. Заведений — М.: Издательский центр «Академия», 2006.-240 с.
- Оценка возможностей привода железнодорожной тележки грунтово-железнодорожного транспортного средства типа МАЗ-547 от собственного двигателя / Д. А. Свечников, Н. А. Кузьмин, Р. М. Чумаев [и др.]. — Текст: непосредственный // Молодой ученый. — 2020. — № 31 (321). — С. 32–39.







