In this article the authors analyses influence factors of Russian oil export to China.
Keywords: China, influence factors, oil export.
The energy sector, particularly the oil industry, plays a special role in Sino-Russian cooperation. Rapidly growing GDP in the People's Republic of China, not well-developed energy saving system, environmental problems and relatively low energy using of its own resources lead to the fact that China needs additional sources of energy supplies. In these conditions, the Russian Federation is an important partner for the People's Republic of China, and the Chinese market is beneficial for Russia, whose leadership is faced with the task of diversifying energy exports, particularly crude oil, and its expansion to the East is extremely profitable.
The steady economic growth of China makes new demands on Russia's foreign economic policy. To strengthen its economic positions in the world, it is becoming increasingly necessary to build up its presence in the Asian part of the continent. In recent decades, regardless of the situation in world energy prices, in most of the countries of the Asia-Pacific region, there has been an increase in demand for oil, while the volume of oil production remains practically unchanged. Although Russia has a large energy potential and has a high share of exports in the production of energy resources, and China is the largest global market for oil consumption, oil supplies from the Russian Federation in this promising direction do not yet satisfy the full potential of Russian oil.
- Influence factors of Russian oil export
To conduct the research we collected the data for 9 biggest importer countries of Russian oil for the period 2001–2019 [3]: China, Netherlands, Germany, Republic of Korea, Italy, Poland, Finland, Japan, Slovakia.
(1) The amount of oil export
The variable (named «oil») represents the amount of crude oil exported to 9 countries from Russia for the period from 2001 to 2019 and is measured in US$. The data is taken from the Trading Economics website according to HS code 2709 [4].
(2) Economy scale
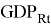
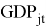
(3) Population
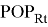
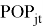
(4) Distance
Distance represents the distance between the capitals of the two countries. Distance in this case is a variable that did not change with time, so the variable of distance is fixed throughout the study period. In this article, we still use simple geographic distances to get better estimation results and is measured in km.
(5) Dummy variable
Contig is added as a dummy variable in the model. Contig represents the common border, indicating whether the two countries are adjacent or bordering. If the two countries have a common border, then we take 1; otherwise take 0. The volume of trade between countries that share a common border will increase because the common border makes transportation costs relatively low.
We select Russia's crude oil export as the research object and construct the model as follows [1]:
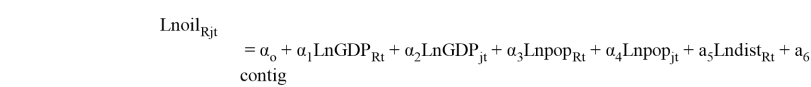
In the model,
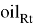
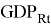
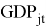
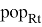
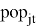
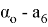
This research will use the nominal exchange rate instead of price according to the research of Brun, Carrere, Guillaumont and De Melo [2].
The fixed effects model assumes that explanatory variables are related to unobservable individual effects, so some variables cannot be taken into account. The random effects model assumes that unobservable individual effects are randomly distributed and uncorrelated with explanatory variables. Here is a simple form of these two effects:
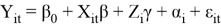
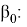
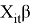
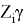
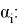
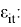
In addition to the trade volume in the study, here are other variables that affect Russia's crude oil exports, such as changes in political relations and preferences of trading partner country. Due to the lack of some data and adding more variables will make the model more complicated, not all variables can be added to the model.
This paper uses fixed ((FE) effects and random (RE) effects to regress panel data, and test the regression results for mutual robustness.
Table 1. FE and RE coefficients and S. E.
|
Variable |
loil (coefficient and standard error) |
|
|
FE |
RE |
|
|
lGDPimp |
0.3788353* (0.2029935) |
0.5259289*** (0.1784061) |
|
lGDPexp |
0.8654615*** (0.1364335) |
1.024278*** (0.1259418) |
|
ldist |
0 |
-1.158255** (0.5808699) |
|
lpopimp |
9.082534*** (3.242843) |
0.0934848 (0.3014497) |
|
lpopexp |
-28.26738*** (9.644309) |
-16.77018* (8.946694) |
|
contig |
- |
-0.2646308 (0.7012011) |
|
C |
362.1067 (167.0037) |
309.4472 (168.9807) |
|
N |
171 |
171 |
|
R |
0.0234 |
0.6283 |
***p0,01, **p0,05, *0,1
Source: author’s calculations
The F statistic value of the fixed effects model is 105.58 rejects the null hypothesis at the 5 % test level, indicating that the fixed effects model is significant. The chi-square statistic of the random effects model is 402.30, rejecting the null hypothesis at the level of 5 %, indicates that the random effects model is significant. Finally, the Hausman test is used to determine whether the fixed effects model or the random effects model should be selected. The value of the chi-square statistic of Hausman test is 0.06, and the acceptance null hypothesis should be used at the level of 5 %, indicating that the random effects model should be selected. The Hausman test results are shown in Table 2.
Table 2. Hausman test results
|
Variable |
Coefficient |
|||
|
FE |
RE |
Difference |
S.E |
|
|
lGDPimp |
0.3788353 |
0.5259289 |
-0.1470936 |
0.0968381 |
|
lGDPexp |
0.8654615 |
1.024278 |
-0.1588164 |
0.0524669 |
|
lpopimp |
9.082534 |
0.0934848 |
8.989049 |
3.228802 |
|
lpopexp |
-28.26738 |
-16.77018 |
-11.4972 |
3.601299 |
Source: author’s calculations
Since the fixed-effect model cannot estimate the influence of variables that do not change with time, in this analysis, it is found that the direction of the significant change of the coefficient under the fixed-effect and random-effect models is consistent, so here we refer to the random effect model.
Russia’s GDP and the GDP of other trading partner countries have a significant positive impact on Russia’s crude oil exports, indicating that the larger a country’s economic scale, the larger its oil trade volume also. In addition, it can be seen that there is a significant negative influence of the Russian population on the oil export, mainly because the increase in the size of its population will lead to an increase in domestic oil demand, and thus its export volume will decrease. Partner’s population has a positive influence on oil trade, and it can be due to the fact that on the one hand, as the population of a country increases, the increase in domestic demand will increase the purchasing power and lead to the increase in oil needs.
The distance between Russia and trading countries indicates that the cost of trade abduction caused by the distance will cause a decrease in Russian crude oil trade. The border also has a positive impact on oil trade indicating that common border reduces additional costs and raises trade volume.
- Conclusion
The factors influencing oil export from Russia to China are in favor of developing and strengthening the relationship in oil field and both countries in the future are able to fulfil each other’s economic and energy needs. Russia and China have a common border and distance between the regions from where oil is exported, the growing GDP of both countries also has a certain positive effect on oil trade.
The Sino-Russian energy relationship has not reached the level of development which their geographical proximity and economic complementariness implies. China and Russia appear to be a perfect match. China is seeking «security of supply» and the diversification of its imports; Russia is pursuing «security of demand» and the diversification of its exports. However, the development of the infrastructure is necessary for the cost-effective delivery of large volumes of oil.
References:
- Bergeijk, P.A., Brakman, S., The gravity model in international trade: Advances and applications, Cambridge University Press, 2010.
- Brun, J-F, Carrere, C, Guillaumont, P and De Melo, J (2005) «Has distance died? Evidence from a panel gravity model», The World Bank Economic Review, 19(1).
- Export value of crude oil from Russia in 2019, by major country of destination. Statista. 2020 URL: https://www.statista.com/statistics/1100591/russia-main-crude-oil-export-destinations/ (accessed on October 11, 2020)
- Russia exports of crude oil. Trading Economics. 2020. URL: https://tradingeconomics.com (accessed on October 11, 2020)
- The World Bank data. 2020. URL: https://data.worldbank.org/ (accessed on September 11, 2020)







