В данной статье рассмотрены особенности интеллектуальных способностей учеников, обоснована необходимость индивидуально находить подход ученику при изучении той или иной темы. Особое внимание уделяется формированию такого когнитивного стиля, как поленезависимость, который связан с высоким показателем невербального интеллекта (образным мышлением) и более высокой обучаемостью, посредством элективного курса по геометрии.
Ключевые слова: когнитивные технологии в обучении, полезависимость, элективный курс, уроки математики, методика преподавания математики, формирование поленезависимости.
Изучение индивидуальных различий в когнитивной сфере традиционно является одной из острейших проблем психологии. Когнитивно-стилевой подход является одной из форм анализа интеллектуальных возможностей человека. Кто-то решает быстро, но может быть делает это не очень качественно, а кто-то медленно, но добивается большей правоты. Кому-то больше даются точные науки, кому-то гуманитарные, поэтому по утверждению сторонников когнитивно-стилевого подхода важно именно каким образом достигается решение [1].
В современной зарубежной и отечественной литературе можно встретить описание около двух десятков различных когнитивных стилей. Среди большого набора психологических характеристик личности можно выделить те, которые в наибольшей степени существенны в индивидуальной познавательной деятельности учащихся и определить 2 когнитивных стиля: полезависимость — поленезависимость.
Изучение математики, а в частности стереометрии, не вызывает у учащихся высокой мотивации, очень трудно пробудить у них интерес к геометрии. Для этого нужно найти индивидуальный подход к каждому ученику, чтобы любой мог свободно ориентироваться в «море» математических построений, чтобы предмет не был в тягость, а наоборот, заинтересовал и подтолкнул к изучению стереометрии. Чтобы оказать помощь учащимся в ходе поиска решения каждой конкретной задачи, следует выявить их индивидуальные способности и возможности принятия информации. А для этого предлагаю учитывать когнитивные стили, которые помогут учителю в выборе того или иного решения задачи для каждого ученика. У каждого человека присутствует своё, индивидуальное сочетание этих стилей, обуславливающих его мыслительную деятельность и ее результаты.
С помощью теста включённых фигур [2] измеряется такой параметр, как полезависимость-поленезависимость (ПЗ — ПНЗ). Поленезависимость связана с высоким показателем невербального интеллекта (образным мышлением), более высокой обучаемостью, успешностью решения задач на сообразительность, легкостью смены установок, с автономностью, стабильностью образа Я, более объективными подходами к проблемам, устойчивостью к внушению, критичностью, более высокой моральностью. [1]
Как определить?
Для того, чтобы выяснить, к какому стилю относится ученик было проведено тестирование. В нем приняло участие 22 ученика 11 класса МБОУ СОШ № 3 г. Уссурийска. Им было предложено пройти тест включенных фигур по методике «Фигуры Готтшальдта» [2].
Ученикам предложили пройти электронную версию либо печатную, все выбрали первый вариант. Испытуемым в данном тестировании предлагается в тридцати замаскированных фигурах найти одну из пяти эталонных фигур и указать ее. Сложные фигуры предъявляются по одной. Фиксируется общее время выполнения задания. После предъявления инструкции следует демонстрация примеров с указанием правильных ответов.
Инструкция
В каждом сложном рисунке имеется один из следующих элементов:
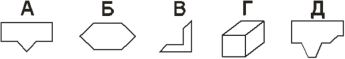
Назовите в каждом случае, какой из этих элементов содержится в рисунке. Например:

Результат
Подсчет сырых баллов производится в соответствии с ключом, приведенным в таблице 1:
Таблица 1
|
1. А |
6. В |
11. Б |
16. Д |
21. Г |
26. Б |
|
2. Б |
7. А |
12. А |
17. А |
22. Б |
27. А |
|
3. В |
8. В |
13. А |
18. Д |
23. Г |
28. Д |
|
4. Г |
9. Д |
14. В |
19. Б |
24. А |
29. В |
|
5. В |
10. Д |
15. Б |
20. В |
25. Д |
30. Б |
За каждый правильный (совпадающий с ключом) ответ присваивается 1 балл.
Индекс полезависимости рассчитывается по формуле:
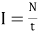
Если I больше 2,5, то можно делать вывод о выраженной поленезависимости.
Если I меньше 2,5, то можно делать вывод о выраженной полезависимости [2].
Таким образом, чем больше правильно выполненных заданий и меньше время работы с тестом, тем более выражена поленезависимость.
Результаты тестирования приставлены в таблице 2.
Таблица 2
|
Номер ученика |
Балл |
Намерен сдавать проф. матем (да/нет) |
Номер ученика |
Балл |
Намерен сдавать проф. матем (да/нет) |
|
1 |
3,2 |
Да |
12 |
1,3 |
Нет |
|
2 |
2,25 |
Да |
13 |
1,24 |
Да |
|
3 |
2,12 |
Нет |
14 |
1,2 |
Нет |
|
4 |
2,1 |
Нет |
15 |
1,13 |
Да |
|
5 |
2,04 |
Да |
16 |
1,11 |
Нет |
|
6 |
1,95 |
Да |
17 |
1,6 |
Да |
|
7 |
1,8 |
Да |
18 |
1,06 |
Да |
|
8 |
1,75 |
Да |
19 |
1,01 |
Да |
|
9 |
1,6 |
Нет |
20 |
0,93 |
Нет |
|
10 |
1.55 |
Да |
21 |
0,92 |
Да |
|
11 |
1,3 |
Нет |
22 |
0,62 |
Нет |
После тестирования ученикам с наиболее высокими баллами и ученикам, собирающимся сдавать профильную математику, предложила посетить элективный курс по геометрии.
Сформировалась небольшая группа, а именно ученики из таблицы 3:
Таблица 3
|
№ |
Ученик |
Балл |
Пол (м/ж) |
|
1 |
Ученик 1 |
3,2 |
Ж |
|
2 |
Ученик 2 |
2,25 |
М |
|
3 |
Ученик 3 |
2,12 |
М |
|
4 |
Ученик 5 |
2,04 |
М |
|
5 |
Ученик 6 |
1,95 |
Ж |
|
6 |
Ученик 7 |
1,8 |
М |
|
7 |
Ученик 8 |
1,75 |
Ж |
|
8 |
Ученик 10 |
1,55 |
Ж |
|
9 |
Ученик 13 |
1,24 |
М |
|
10 |
Ученик 18 |
1,06 |
М |
|
ИТОГО:10 учеников, из них девочек — 4, мальчиков — 6. |
|||
Проведённое первичное тестирование показало, что в данном классе один ученик с выраженной поленезависимостью, причем с высоким баллом, треть учеников близки к поленезавимости, а остальные явно полезависимы. Некоторые ученики так сильно хотели ответить на все задания верно, что забыли о таком критерии, как время выполнения, поэтому это учитывалось при наборе в группу (таблица 3) для проведения элективного курса.
Так как элективные курсы выбираются самими учащимися, они должны соответствовать их потребностям, целям обучения и мотивам выбора курса. Следует отметить, что к основным мотивам выбора элективных курсов в 10–11 классе, которые следует учитывать при разработке и реализации элективных курсов относятся: подготовка к ЕГЭ по профильным предметам; приобретение знаний и навыков, освоение способов деятельности для решения практических, жизненных задач, уход от традиционного школьного «академизма»; поддержка изучения базовых курсов; профессиональная ориентация [3]. Так и в разработанном элективном курсе по геометрии для 11 класса «Векторно-координатный метод решения задач стереометрии» все это учитывалось. Элективный курс расширяет базовый курс по математике, дает более глубокие знания, связанные с понятием вектор в пространстве, способствует более полному усвоению векторно-координатного метода в стереометрии. Данный курс посвящен систематическому изложению учебного материала, связанного с понятием ненулевого вектора и аспектами его применения. Элективный курс вызывает познавательный интерес учащихся, способствует интеллектуальному развитию личности, тем самым развивает когнитивные способности, а особенно такой важный в обучении когнитивный стиль, как поленезависимость.
Данное событие можно заметить после повторного тестирования на полезависимость/поленезавимость. В нем приняло участие 22 ученика 11 класса МБОУ СОШ № 3 г. Уссурийска. Им было предложено снова пройти тест включенных фигур по методике «Фигуры Готтшальдта».
Результаты тестирования приставлены в таблице 4.
Таблица 4
|
Номер ученика |
Балл в первичном тестировании |
Балл в повторном тестировании |
Номер ученика |
Балл в первичном тестировании |
Балл в повторном тестировании |
|
1 |
3,2 |
3,3 |
12 |
1,3 |
1,3 |
|
2 |
2,25 |
2,4 |
13 |
1,24 |
1,4 |
|
3 |
2,12 |
2,35 |
14 |
1,2 |
1,2 |
|
4 |
2,1 |
2,05 |
15 |
1,13 |
1,1 |
|
5 |
2,04 |
2,0 |
16 |
1,11 |
1,2 |
|
6 |
1,95 |
2,2 |
17 |
1,06 |
1,0 |
|
7 |
1,8 |
2,15 |
18 |
1,06 |
1,9 |
|
8 |
1,75 |
2,2 |
19 |
1,01 |
1,1 |
|
9 |
1,6 |
1,5 |
20 |
0,93 |
0,9 |
|
10 |
1.55 |
1,6 |
21 |
0,92 |
1,0 |
|
11 |
1,3 |
1,2 |
22 |
0,62 |
0,6 |
*Жирным выделена группа, которая прошла элективный курс
Проведённое вторичное тестирование показало, что в данный элективный курс повысил балл на 0,2/0,3, а у ученика № 18 на 0,8 (в первичном тестировании у этого ученика большое количество времени ушло на тестирование, во втором время сократилось почти вдвое). Предполагаю, что это связано с тем, что курс повышает способность к пространственному мышлению, что помогло быстрее пройти тест, если и были ошибки в выполнении заданий, то скорость решения это компенсировала, т. к. является важным фактором. Контрольная группа почти без изменений: выше/ниже на 0,1.
Подводя итог всей работы, которая направлена повышение когнитивных способностей, находим подтверждение того, насколько элективные курсы незаменимы для достижения основных целей образования. С хорошо разработанной системой элективных курсов каждый ученик может получить образование с определенным желаемым уклоном в ту или иную область знаний.
Литература:
- Когнитивные стили [Электронный ресурс] — Режим доступа: URL: http://www.psyworld.ru/for-students/stories-for-students/571–2008–12–12–21–08–08.html
- Тест включённых фигур [Электронный ресурс] — Режим доступа: URL: https://ru.wikipedia.org/wiki/Тест_включённых_фигур
- Рытченко, И. Н. Роль элективных курсов в системе подготовки учащихся к ЕГЭ / И. Н. Рытченко. — Текст: непосредственный // Молодой ученый. — 2019. — № 15 (253). — С. 292–294. — URL: https://moluch.ru/archive/253/58105/







