В данной работе проведен анализ работы системы фазовой автоподстройки частоты. Рассмотрены реакции схемы на скачок фазы, частоты, и на линейное изменение частоты. Показано, что большинство контуров фазовой автоподстройки частоты имеет второй порядок. Рассмотрены и оценены условия стабилизации фазы, влияние дополнительных факторов на систему синхронизации.
Ключевые слова: ФАПЧ, фазовая синхронизация.
Актуальность
В последние десятилетия были предложены различные методы удаленной фазовой синхронизации. Одним из основных элементов систем фазовой синхронизации является контур фазовой автоподстройки частоты (ФАПЧ). Современные спутниковые аппаратуры характеризуются низким отношением сигнал-шум, наличием изменяющегося во времени доплеровского сдвига частоты и других мешающих факторов, что обуславливает рост фазовой ошибки в контуре ФАПЧ [1, 3]. Поэтому задача повышения устойчивости контура ФАПЧ систем синхронизации к действию мешающих факторов в настоящее время весьма актуальна.
Цель работы — разработать реакции системы ФАПЧ на скачок фазы, частоты, и на линейное изменение, а также оценить условия стабилизации фазы, влияние порядка передаточной функции петлевого фильтра на систему синхронизации.
Структурная схема и принцип работы системы ФАПЧ
Практически во всех схемах синхронизации имеется определенная разновидность контура фазовой автоподстройки частоты.
Контур фазовой автоподстройки частоты — это система управления, в которой регулируемая переменная является фазой периодического сигнала. В принципе, ФАПЧ состоит из трех основных компонентов: фазового детектора, контурного фильтра и генератора, управляемого напряжением (ГУН). Когда контур заблокирован, управляющее напряжение таково, что фаза ГУН равна фазе входного сигнала фазового детектора [2,4,6]. Сигнал, генерируемый фазовым детектором, вводится в контурный фильтр для генерации управляющего напряжения, которое подается на ГУН. Петлевой фильтр имеет передаточную функцию нижних частот, и его порядок определяет порядок петли.
Схематическая диаграмма основы контура ФАПЧ показана на рис. 1.
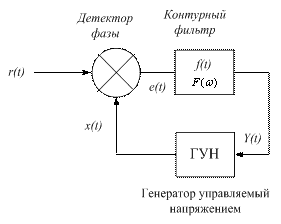
Рис. 1. Схема контура фазовой автоподстройки частоты
Контуры ФАПЧ самоуправляемы, причем управляющим параметром является фаза локально генерируемой копии поступающего несущего сигнала.
Рассмотрим нормированный входной сигнал следующего вида:
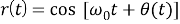
где
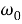
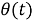
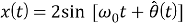
На выходе детектора фазы эти сигналы дадут выходной сигнал:
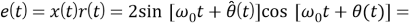
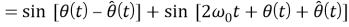
Напряжение с удвоенной частотой принимаемого сигнала на выходе фазового детектора подавляется фильтром низких частот и можно пренебречь. Фильтр нижних частот дает сигнал рассогласования, являющийся функцией исключительно разности фаз между входом (формула (1)) и выходом ГУН (формула (2)). Выходная частота ГУН является производной по времени от аргумента синусоиды из уравнения (2). Если предположить, что
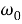
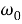
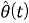
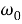
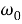
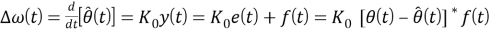
Где
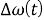
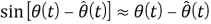
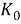
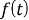
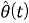
Теорема об окончательном значении преобразования Фурье формулируется следующим образом.
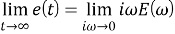
Известно, что
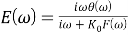
Объединяя уравнения (5) и (6), получаем:
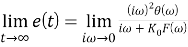
Реакция на скачок фазы
Рассмотрим отклик контура, находящегося в стационарном состоянии, на скачок фазы на входе контура.
Предположим, что изначально контур ФАПЧ синхронизирован по фазе с входным сигналом, а скачок фазы вывел его из этого состояния. Причем после резкого изменения входная фаза снова стала стабильной. Вообще, это самый простой случай, с которым способен справиться контур ФАПЧ. Итак, Фурье-образ скачка фазы равен следующему:
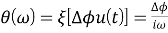
Здесь
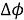
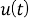
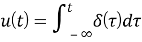
где
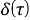
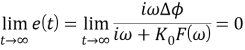
в предположении, что
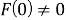
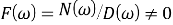
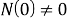
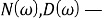
Реакция на скачок частоты
Рассмотрим отклик контура, находящегося в стационарном состоянии, на скачок частоты на входе.
Посредством скачка частоты можно аппроксимировать последствия доплеровского смещения частоты входного сигнала вследствие относительного движения передатчика и приемника. Следовательно, данный пример важен для систем с мобильными терминалами. Поскольку фаза является интегралом частоты, при постоянном сдвиге входной частоты входная фаза (как функция времени) будет меняться линейно. Фурье-образ фазовой характеристики — это Фурье-образ интеграла частотной характеристики. Поскольку частотная характеристика — это ступенчатая функция, а образ интеграла — это образ подынтегрального выражения, деленного на параметр
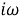
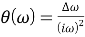
где
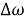
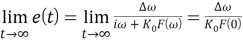
В данном случае стационарный результат зависит не только от ненулевой постоянной составляющей в характеристике, но и от других свойств контурного фильтра. Если фильтр является «всепропускающим» (широкополосным с полосой, равной бесконечности), то:
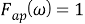
Если фильтр является фильтром нижних частот, то:
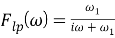
Если фильтр является стабилизирующим, то:
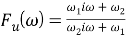
Уравнение (10) показывает, что контур отследит изменение входной фазы с установившейся ошибкой, величина которой зависит от члена
К
0 и величины скачка частоты. Подстановка любого из значений
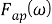
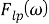
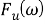
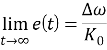
Отметим, что произведение нескольких фильтров с характеристиками, подобными указанным в формулах (11), (12) или (13), по-прежнему будет давать желаемый результат. Стационарная ошибка, называемая
ошибкой по скорости,
будет существовать вне зависимости от порядка фильтра, если только знаменатель
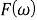
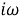
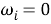
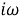
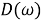
Реакция на линейное изменение частоты
Рассмотрим отклик контура, находящегося в стационарном состоянии, на линейное (по времени) изменение частоты на входе.
Ситуация, описанная в данном примере, соответствует ступенчатому изменению производной по времени от входной частоты. Это может, например, аппроксимировать изменение скорости доплеровского смещения, что позволило бы смоделировать ускорение относительного движения спутника (или самолета) и наземного приемника. В данном случае Фурье-образ фазовой характеристики дается следующим выражением:
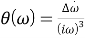
Здесь
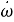
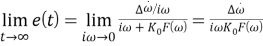
Если контур имеет ненулевую ошибку по скорости (т. е. если правая часть уравнения (10) не равна нулю), уравнение (15) показывает, что стационарная фазовая ошибка становится неограниченной вследствие линейного изменения частоты. Это означает, что контур ФАПЧ с контурными фильтрами, характеристики которых описываются уравнениями (11) — (13), не сможет отследить линейное изменение частоты. Чтобы все-таки отследить это изменение, знаменатель преобразования контурного фильтра
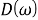
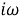
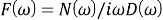
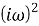
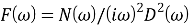
Ниже приведены схемы ФАПЧ в Simulink для моделирования и графики полученных результатов при различных значениях порядка фильтра (фильтр 1-ого, 2-ого и 3-его порядка).
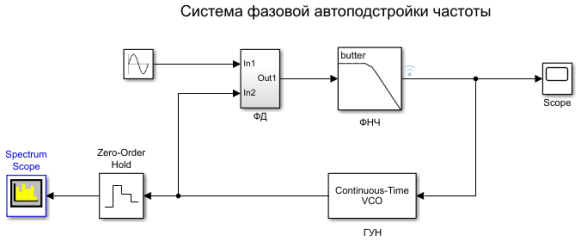
Рис. 2. Схема ФАПЧ для моделирования в Simulink
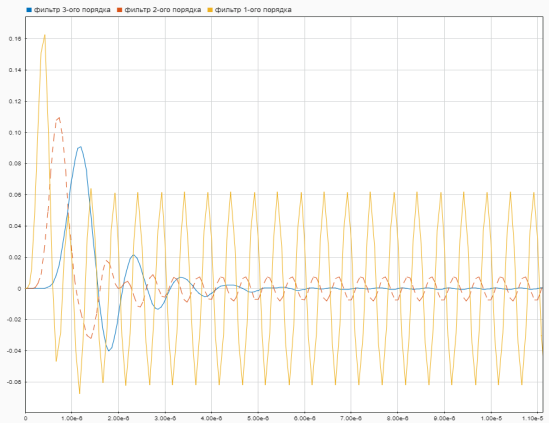
Рис. 3. Сигналы на выходе фазового детектора, при различных значениях порядка фильтра
Основные выводы
Во всех случаях синхронизация частоты получается с помощью контура на один порядок ниже, чем необходимо для синхронизации фазы. Итак, анализ стационарной ошибки является полезным показателем требуемой сложности контурных фильтров.
На практике подавляющее большинство контуров ФАПЧ имеет второй порядок. Это объясняется тем, что контур второго порядка можно спроектировать безусловно устойчивым. Безусловно устойчивые контуры всегда будут пытаться отследить входной сигнал. Никакие входные условия не приведут к тому, что контур будет реагировать на изменения входа в ненадлежащем направлении. Контуры второго порядка отследят последствия скачка частоты (доплеровского смещения); кроме того, они относительно просто анализируются, поскольку аналитические выражения, полученные для контуров первого порядка, являются хорошей аппроксимацией для контуров второго порядка. Контуры третьего порядка применяются в некоторых специальных областях, например некоторые навигационные приемники систем GPS (Global Positioning System — глобальная система навигации и определения положения) и некоторые авиационные приемники. В то же время характеристики таких контуров относительно сложно определить, кроме того, контуры третьего и более высоких порядков являются только условно устойчивыми. Если же вследствие динамики сигнала для когерентной демодуляции потребуются контуры третьего и более высоких порядков, то вместо этого используется некогерентная демодуляция.
Литература:
- Цифровые радиоприемные системы: Справочник / Под ред. М. И. Жодзишского. — М.: Радио и связь, 1990, 208 с.
- John L.Stensby Phase-Locked Loops — Theory and Applications . University of Alabama in Huntsville, 1997, 377с.
- Mengali U. and D'Andrea A. N. Synchronization Technique for Digital Receivers. Plenum Press, New York, 1997.
- F. M. Gardner. Can Analog PLLs Hold Lock? A Paradox Explored. Circuits and Systems Magazine, IEEE , 7(3):46 –52 с, quarter 2007.
- Gardner F. M. Phaselock Techniques. 2nd ed., John Wiley & Sons, Inc., New York, 1979.
- Ван Трис Г. Теория обнаружения, оценок и модуляции. Том 2. М., «Сов. радио», 1975, 344 с.







