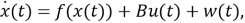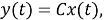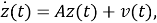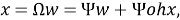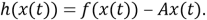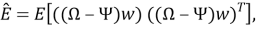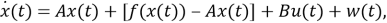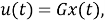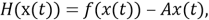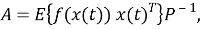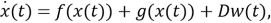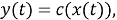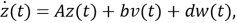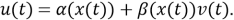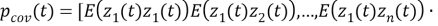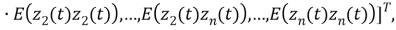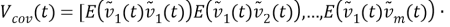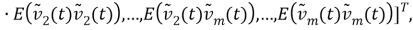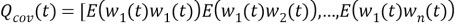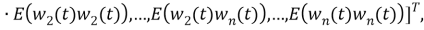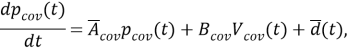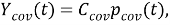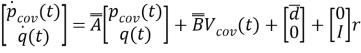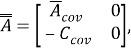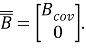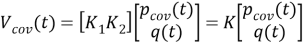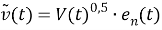Подход к ковариантному управлению нелинейными стохастическими системами с ковариационной обратной связью



В данной работе исследуется алгоритм ковариационного управления нелинейными стохастическими системами с использованием ковариационной обратной связи. Поэтому предлагаемый алгоритм ковариационного управления выводится для нашего случая сначала путем применения метода ковариационного управления и линейной аппроксимации нелинейных систем, а затем достигается путем принятия этого метода для класса нелинейных стохастических систем, использующих идею линеаризации обратной связи и ковариационного регулятора обратной связи.

Ключевые слова: обратная связь, ковариационное управление, нелинейная система, ковариационная обратная связь.

Введение

Большинство представленных подходов, анализирующих динамику стохастических систем, используют алгоритм ковариационного управления для разработки правила, обеспечивающего ограниченные желаемые ковариационные цели. Дисперсия случайной величины очень важна в большинстве контрольных исследований, таких как анализ систем прогнозирования и задачи оценки состояния. Многие исследователи провели огромную работу, чтобы обеспечить сходимость в системах идентификации и оценки [1, 2], фильтрации данных обнаружения и диагностики неисправностей [3] или иметь лучшую скорость сходимости некоторых интеллектуальных алгоритмов, таких как генетический алгоритм [4] и нейронная сеть [5]. Неправильный выбор дисперсии может привести к нестабильности всей системы и снизить ее производительность.

Большинство работ по ковариационному назначению сосредоточены на теории назначения ковариаций состояний (SCA) для линейных систем. В этих исследованиях предполагались первичные цели контроля, такие как ограничения дисперсий состояний. Кроме того, для входных значений дисперсии можно было бы предположить вторичные цели.

Поскольку отчеты для нелинейных случайных систем немногочисленны, исследователи заинтересованы в применении теорий линейных систем для нелинейных случаев, насколько это возможно, без потери слишком большой точности и производительности.

В данной работе исследуется алгоритм ковариационного управления нелинейными системами с использованием ковариационной обратной связи. В соответствии с идеей линеаризации обратной связи и ковариационной обратной связи доказано, что любую желаемую ковариационную матрицу можно поместить в соответствующую ей нелинейную систему.

Предварительные условия и постановка задачи

В этом разделе для получения линеаризованной аппроксимации нелинейных систем приводятся две идеи линеаризации, включающие линейную аппроксимацию нелинейных стохастических систем и точную линеаризацию нелинейных стохастических систем с обратной связью.

1. Линейная аппроксимация нелинейных стохастических систем.

Рассмотрим общую нелинейную стохастическую систему с нулевым средним значением:

(1)

где является нулевым значением белого шума и имеет ковариацию и является нечетной функцией относительно , таким образом, все средние значения равны нулю. Данную систему также можно рассматривать как функцию отображения, такую как . Линейная аппроксимация общей системы, представленная Лейтхедом [7, 8] в уравнении (1) может быть рассмотрена в следующем виде:

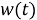
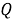
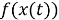
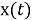
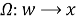
(2)

а соответствующая функция отображения определяется как: . Связь между и определяется следующим образом [7, 8]:

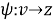
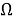
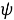
(3)

где нелинейный оператор связи, определяемый следующей функцией [10]:

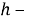
(4)

Лейтхед доказал, что линейная система является приемлемым представлением нелинейной системы , когда ковариационная матрица ошибок мала, где

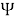
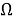
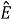
(5)

где оператор математического ожидания.

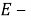
В дальнейшем подходящий оптимальный выбор для нелинейной системы может быть достигнут, когда нелинейности системы заменяются их стохастическими входными характеризующими функциями:

(6)

с нелинейной функцией связи

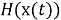
(7)

где матрица может быть вычислена по следующему уравнению:

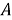
(8)

где оператор математического ожидания, а стационарная ковариация состояний. Основная проблема этого метода заключается в том, что полученная оценка нелинейной стохастической системы с параметрами точности оценивания зависит от матрицы ковариации состояний системы.

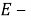
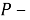
2. Точная линеаризация нелинейных стохастических систем с обратной связью.

Использование метода обратной связи по состоянию и замены переменных, преобразующего нелинейную систему в эквивалентную линеаризованную систему, является одной из наиболее часто используемых идей практического проектирования нелинейного управления [9].

Рассмотрим более общую форму нелинейной стохастической системы с нулевым средним значением:

(9)

где гладкие векторные поля. Кроме того, это вектор состояния, входной вектор, белый шум и выходной вектор системы соответственно.

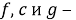
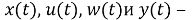
В методе линеаризации входного состояния проблема линеаризации обратной связи будет решена в два этапа.

Сначала рассмотрим преобразование состояния и входное преобразование таким образом, что нелинейная динамика системы будет преобразована в линейную динамику, не зависящую от времени, в следующей форме:

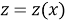
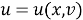
(10)

где

(11)

Затем при проектировании используются стандартные линейные методы управления (например, размещение столбов). Итак, используя разработанную обратную связь линеаризации и подходящее преобразование состояния, проблема ковариационного управления и стабилизации нелинейной системы (9) станет проблемой стабилизации и ковариационного управления с новой линейной динамической системой (10) с входом .

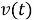
В отличие от большинства распространенных методов размещения ковариационной матрицы для линейных или нелинейных систем, мы можем рассматривать вопрос отслеживания выходных данных системы одновременно с ковариационным управлением.

Учитывая, что большинство нелинейных систем может быть преобразовано в эквивалентную линейную систему с помощью линеаризуемой обратной связи, идея ковариации обратной связи может быть использована для управления большинством нелинейных систем.

Описание системы ковариаций и устройство регулятора ковариации

1. Описание системы ковариации.

Пусть вектор состояний, дополнительный управляющий вход, и вектор технологического шума, соответственно.

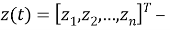
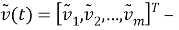
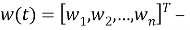
		(12)
		(13)
		(14)

В результате, система динамической ковариации может быть сведена к стандартному пространству состояний модели путем определения , , и следующим образом [6]:

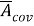
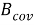
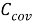
(15)

где и элементы матрицы состояний и возмущений предлагаемой ковариационной системы в пространстве состояний, соответственно, и вычисленные на основе нелинейного отображения. Кроме того, является детерминированным, и мы можем принять его как фактор возмущения.

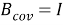
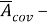
Следует отметить, что, хотя модель является стохастической, данная ковариационная модель в пространстве состояний (15) является детерминированной.

2. Дизайн контроллера ковариации.

Проектирование ковариационной обратной связи (при наложении входного воздействия для управления ковариацией, назначенной в указанной матрице, является основной проблемой.

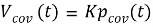
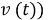
В силу линейности ковариационной системы, представленной в (15) с использованием техники, введенной Халоозаде и Баромандом [21], с интегральным состоянием , новое расширенное пространство состояний определяется как

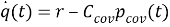
(16)

где определяется как искомый вектор ковариации, и

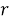
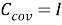
(17)

Управляемость пары

является необходимым условием существования решения задачи ковариационного слежения. Тогда обратная связь по ковариации состояний имеет следующий вид:

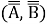
(18)

Из-за регуляризации задачи в исходной системе состояний управляющий сигнал — белый шум со средним нулевым значением и ковариационной матрицей . Поэтому на каждой итерации входной сигнал будет выводиться следующим образом:

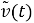
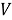
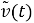
(19)

где обозначается как белый шум.

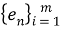
Выводы

Если выбрано малое значение измеряемой матрицы и предполагается сильное фильтрующее действие в статистической линеаризации или идея линеаризации с обратной связью по входному состоянию, нелинейная система может быть определена следующим образом:

Шаг 1 : рассмотреть входное управление преобразованием состояния и обратной связи так, чтобы нелинейная динамика (2) или (9) была перенесена в линейную динамику.

Шаг 2 : онлайн-оценка ковариации состояния основной системы.

Шаг 3 : переставить и изменить вектор ковариации и из (12) и (13).

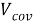
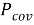
Шаг 4 : вычислить переменную управления ковариацией из ((15) - (18)).

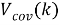
Шаг 5 : модифицировать ковариационную матрицу из , как ковариантности управляющего сигнала .

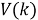
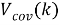
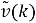
Шаг 6 : сгенерировать сигнал управления ковариацией с ковариационной матрицей

из (19).

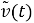
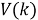
Заключение

В данном исследовании был исследован алгоритм ковариационного управления нелинейными системами с использованием ковариационной обратной связи. Сначала мы показали, что при условии, что линейное приближение нелинейной системы является хорошим представлением нелинейной системы, сценарий ковариационного управления нелинейными системами включает в себя теорию ковариационного управления, основанную на идее ковариационной обратной связи.

Литература:

1. J. Lardies and N. Larbi, «Dynamic system parameter identification by stochastic realization methods», Journal of Vibration and Control, vol. 7, no. 5, pp. 711–728, 2001.
2. V. K. Dertimanis, «On the use of dispersion analysis for model assessment in structural identification», Journal of Vibration and Control, vol. 19, no. 15, pp. 2270–2284, 2013.
3. S. E.-O. Bahlous, M. Abdelghani, H. Smaoui, and S. El-Borgi, «A modal filtering and statistical approach for damage detection and diagnosis in structures using ambient vibrations measurements», Journal of Vibration and Control, vol. 13, no. 3, pp. 281–308, 2007.
4. M. P. Schoen, «Application of genetic algorithms to observer Kalman filter identification», Journal of Vibration and Control, vol. 14, no. 7, pp. 971–997, 2008.
5. J. Latha and N. Devarajan, «Feature extraction of handwritten numeric characters and recognition using an artificial neural network: a new approach», Journal of Vibration and Control, vol. 20, no. 12, pp. 1869–1876, 2014.
6. S. Baromand and H. Khaloozadeh, «On the closed-form model for state covariance assignment problem», IET Control ;eory & Applications, vol. 4, no. 9, pp. 1678–1686, 2010.
7. W. E. Leithead, «Systematic approach to linear approximation of non-linear stochastic systems part 1. Asymptotic expansions», International Journal of Control, vol. 51, no. 1, pp. 71–91, 1990a.
8. W. E. Leithead, «Systematic approach to linear approximation of non-linear stochastic systems part 2. Filtering hypothesis», International Journal of Control, vol. 51, no. 1, pp. 93–117, 1990b
9. K. Khalil Hassan, Nonlinear Systems, Michigan State University, East Lansing, Michigan, 3rd edition, 2003