Численное определение предельно допустимой нагрузки в своде-арке из вальцованного тонкостенного профиля по предельным напряжениям, не приводящее к появлению пластического шарнира и потери устойчивости конструкции .
Ключевые слова: напряжения в гофрированных и прямолинейных элементах арки, быстровозводимые бескаркасные арочные здания, легкие конструкции, ангары, MIC-120.
Numerical determination of the maximum permissible load in the arch-arch of a corrugated U-shaped thin-walled profile when loaded with loads.
Keywords: stresses in corrugated arch elements, stresses when working together straight and curved, MIC-120.
Определив предельно допустимые нагрузки на арочный профиль U образного сечения, смоделируем профиль со следующим сечением-

Материалы и методы: по твердотельной модели, выполненной в программном комплексе Solid Works в виде свода — арки загружаемого до возникновения предельных напряжений и определения распределения напряжений в профиле рис.2–5. Данный профиль рассчитан методом конечных. Загружение приложено к гофрированной нижней полке профиля или на все поперечное сечений (Ry=343232750Н/м2).
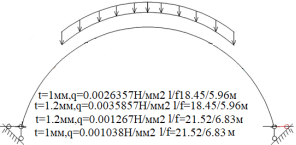
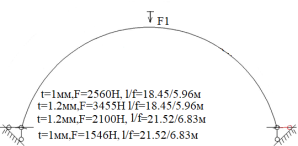


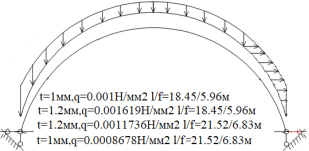
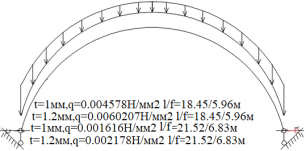
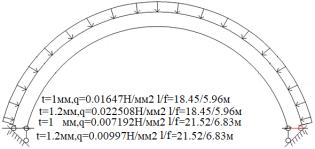
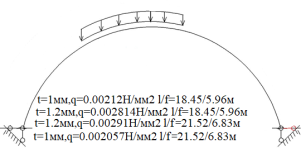
Рис. 1.Сечение/расчетная схема (при рассмотрении свода, не профиля,) закрепление из плоскости отсутствует). Форма загружения и значение предельной нагрузки
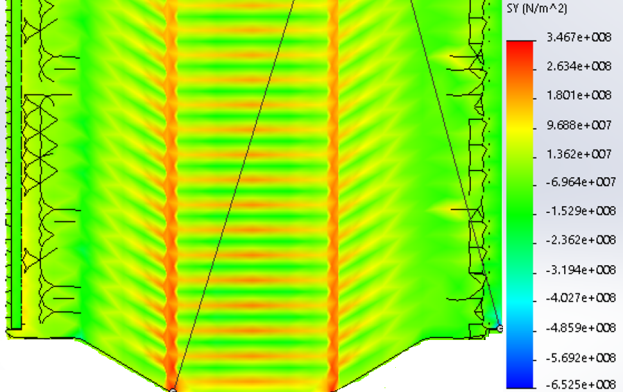
Рис. 2. Эпюра распределения нормальных напряжений при стреле подъема 6,83 м (сосредоточенная сила в максимальной точке подъема давление)
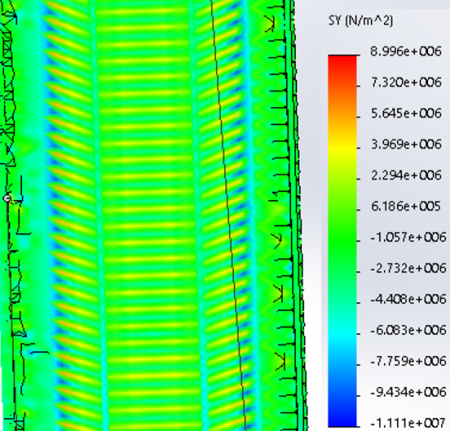
Рис. 3. Эпюра распределения нормальных напряжений при стреле подъема 6,83 м (радиальное давление)
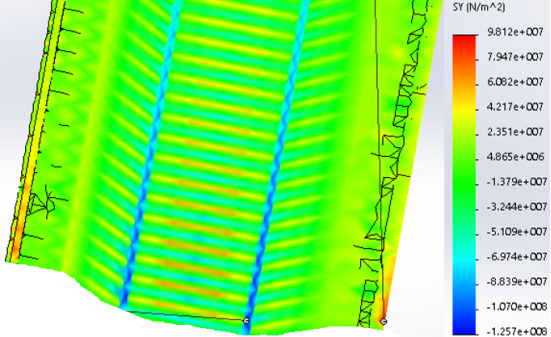
Рис. 4. Эпюра распределения нормальных напряжений при стреле подъема 6,83 м (ветровое давление)
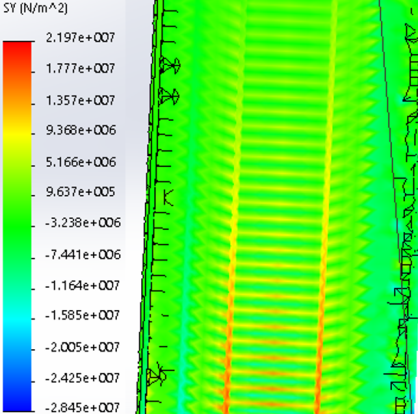
Рис. 5. Эпюра распределения нормальных напряжений при стреле подъема 6,83 м (гравитационное/снеговое давление)
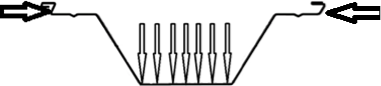
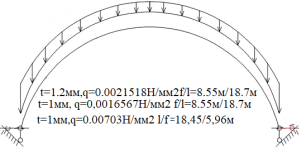
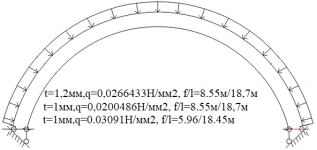
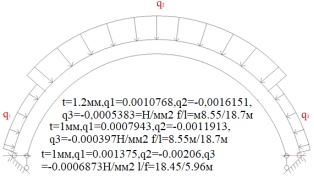
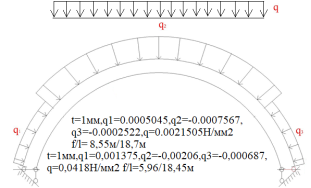
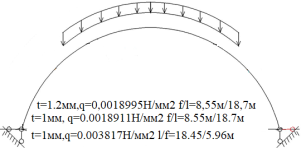
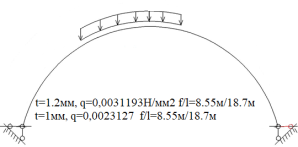
Рис. 6.Сечение/расчетная схема (при рассмотрении свода, не профиля,) закрепление из плоскости отсутствует). Форма загружения и значение предельной нагрузки (Рис.2–5)
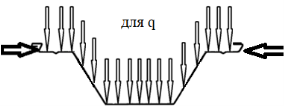
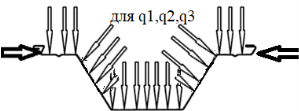
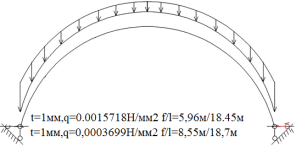
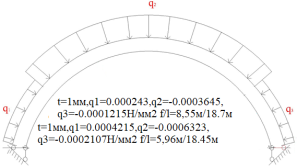
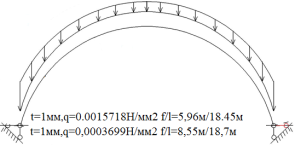
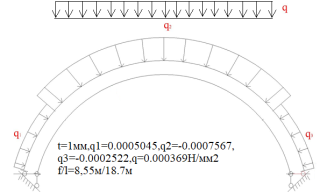
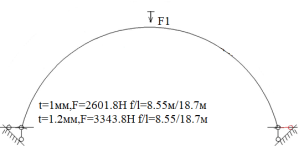
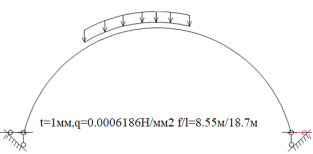
Рис. 7.Сечение/расчетная схема (при рассмотрении свода, не профиля,) закрепление из плоскости отсутствует). Форма загружения и значение предельной нагрузки (Рис.2–5)

Рис. 8.Эпюра распределения нормальных напряжений в узле закрепления вальцованного свода. (при гравитационном давлении) (профили между собой не объединены)
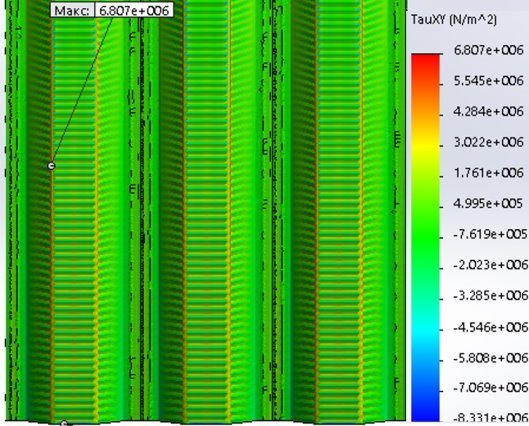
Рис. 9.Эпюра распределения тангенциальных напряжений в узле закрепления вальцованного свода (при гравитационном давлении) (профили между собой не объединены)
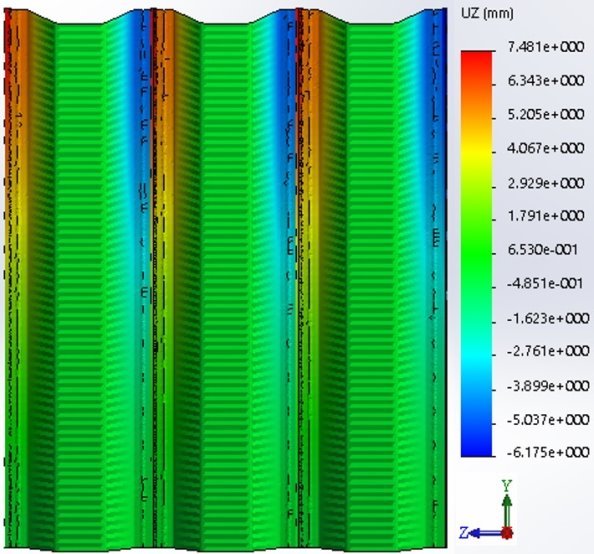
Рис. 10.Эпюра распределения перемещений из плоскости в узле закрепления вальцованного свода (при гидростатическом давлении) (профили между собой не объединены)

Рис. 11.Эпюра распределения нормальных напряжений в узле закрепления вальцованного свода (при гидростатическом давлении) (профили между собой не объединены)

Рис. 12.Эпюра распределения тангенциальных напряжений в узле закрепления вальцованного свода (при гидростатическом давлении) (профили между собой не объединены)
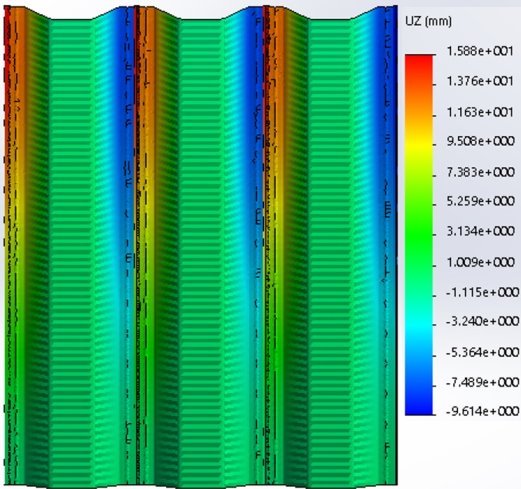
Рис. 13.Эпюра распределения перемещений в узле закрепления вальцованного профиля (профили между собой не объединены) (при гидростатическом давлении)
Таблица 1
(рис. 8–13)
|
Толщина профиля, мм |
Напряжения МАХ, Н/м2 |
Напряжения МIN, Н/м2 |
Напряжения танг МАХ, Н/м2 |
Напряжения танг МIN, Н/м2 |
Величина нагрузки, Н/мм2 |
Перемещения в плоскости, мм |
Перемещения из плоскости, мм |
|
|
0,8 |
7,01E+07 |
-1,03E+08 |
1,30E+07 |
-1,12E+07 |
0,0010025 |
19,8800 |
7,4810 |
гравит |
|
4,59E+08 |
-3,72E+08 |
5,87E+07 |
-4,35E+07 |
0,0010025 |
88,2500 |
35,5900 |
радиа |
|
|
1,2 |
3,75E+07 |
-4,98E+07 |
6,81E+06 |
-8,33E+06 |
0,0010025 |
9,1520 |
3,2400 |
гравит |
|
2,56E+08 |
-1,89E+08 |
2,91E+07 |
-3,04E+07 |
0,0010025 |
41,3300 |
15,8800 |
радиа |
По данному численному расчету рис.1,6,7 можно определить редуцированные геометрические характеристики при радиальной нагрузке
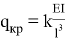
Результаты: численно определили предельно допустимые нагрузки приемлемые при различных загружениях профиля, с закреплением из плоскости показанным на рис.1,6,7. В зависимости от формы загружений предельная нагрузка показана на рис.1,6,7, при работе по данной расчетной схеме с закрепление всего поперечного сечения в узлах закрепления. При работе профиля в своде предельная нагрузка будет иной ввиду податливости профиля из плоскости рис10,13 и отсутствия закрепления показаны на рис.1,6,7. Учитывая распределение напряжений на рис.2–5 от гравитационной равномерно распределенной или не равномерно распределенной нагрузки численно определили, что нижняя полка больше загружена в узлах закрепления, чем стенки или верхние полки. При воздействии радиальной или ветровой нагрузки в верхних полках возникают напряжения численно превышающие значений в нижних полках в узле закрепления. На эпюрах показано неравномерное распределений численного значения положительных и отрицательных напряжения в верхних и нижней полках при разных формах загружений. При нагрузке выше предельно допустимой по напряжениям пластический шарнир не образуется, но после превышения текучести (Ry=203943242.6Н/м2) в полках(е) изменится расчетная схема тонкостенной конструкции, данной влияние сложно учесть в численном расчете [1]. Значение нагрузки возникновения в конструкции текучести можно определить интерполяцией от ранее полученных значений предельных нагрузок по напряжениям.
Обсуждения: арка при изменении соотношения пролета к подъему распределяет напряжения по сечению тонкостенного профиля одинаково, при рассмотрении элемента размером dx на dy на рис.13,15 перемещения из плоскости в верхних полках не одинаковы, что при отсутствии закрепления из плоскости рис.1,6,7 или нагрузке под углом значение предельной нагрузки изменится при влиянии эксцентриситета.
Литература:
- Карабутов М. С. Численное определение критической нагрузки по предельным перемещениям и напряжениям арки из гофрированного U-образного тонкостенного профиля при загружении гравитационной нагрузкой // Молодой ученый. — 2019. — № 43. — С. 19–22.
- Карабутов М. С. Численное определение предельно допустимой нагрузки на свод-арку из гофрированного U-образного тонкостенного профиля. // Молодой ученый. — 2020. — № 10.
- Карабутов М. С. Результаты определения предельно допустимой ветровой нагрузки на свод-арку из гофрированного U-образного тонкостенного профиля. // Молодой ученый. — 2020.№ 14.
- Карабутов М. С. Численное определение предельно допустимой несимметричной нагрузки на свод-арку из гофрированного U-образного тонкостенного профиля. // Молодой ученый. — 2020.№ 18.
- Карабутов М. С. Результаты определения предельно допустимой нагрузки на свод-арку из гофрированного U-образного тонкостенного профиля при разных формах загружений. // Молодой ученый. — 2020.№ 27.
- Л. В. Старцева, В. Г. Архипов, А. А. Семенов СТРОИТЕЛЬНАЯ МЕХАНИКА в примерах и задачах. –М.: Издательство АСВ, 2013. -224 с.
- Карабутов, М. С. Численный анализ работы арки из вальцованного U-образного профиля с результатами численных данных прямолинейного вальцованного металлического тонкостенного профиля // Молодой ученый. — 2019. — № 44 (282). — С. 103–106.







