В статье рассматривается Теорема Пикара — теорема о существовании и единственности решения обыкновенного дифференциального уравнения первого порядка. Приводятся различные формулы, замечания и поэтапные доказательства теоремы Пикара. Сведение уравнения 𝒏-го порядка к нормальной системе. Теорема существования и единственности для уравнений 𝒏-го порядка. Локальная теорема Коши-Пикара дает достаточные условия разрешимости задачи Коши для широкого класса ОДУ. В теории функций комплексного переменного в честь Ш. Э. Пикара названы две теоремы, традиционно называемые большая и малая теоремы Пикара.
Малая теорема Пикара
Формулировка
Областью значений целой функции, отличной от константы, является вся комплексная плоскость, за исключением, быть может, лишь одной точки.
Фактически, малая теорема Пикара является следствием большой, так как, по теореме Лиувилля, целая функция либо является многочленом, либо имеет на бесконечности существенную особенность.
Ключевые слова: теорема Пикара, дифференциальное уравнение, область, неравенство.
Введение:
Рассмотрим обыкновенное дифференциальное уравнение первого порядка:
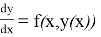
с начальным условием
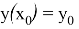
где правая часть (1) определена в замкнутой области R:
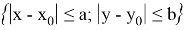
где a и b — некоторые положительные числа.
Замечание 1: Плоскуюобластьбудем называть выпуклой (или правильной) по у, если прямая, параллельная оси Оу, пересекает границу области только в двух точках, а прямая, параллельная оси Ох пересекает границу области в 3 и более точках.
Приведём пример выпуклой (или правильной) области по у:
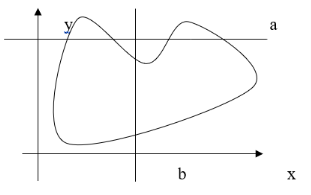
На графике видно, что прямая b, параллельная оси Оу, пересекает границу области только в двух точках, а прямая, а , параллельная оси Ох, пересекает границу этой области в 4 точках. Следовательно, наша область выпукла по у , но не является выпуклой по оси Ох.
Замечание 2: Так как непрерывная функция является в замкнутой области ограниченной, то существует такое положительное число М , что неравенство
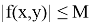
выполняется для всех точек области R; (теорема Вейерштрасса)
Теорема.
Пусть: 1)
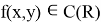
f (x, y) удовлетворяет в области R относительно переменного у
условия Липшица
: существует такое положительное число N, что для любого значения
х
,
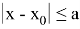
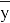
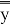
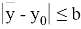
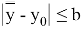
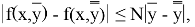
Тогда существует единственное решение уравнения (1):
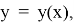
удовлетворяющее начальному условию
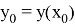
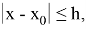
где
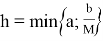
Доказательство теоремы разобьём на ряд этапов:
Этап 1: Сведение задачи Коши к интегральному уравнению из (1) имеем
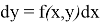
откуда
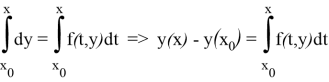
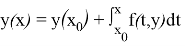
Покажем теперь эквивалентность задач (1), (2) и (5).
Пусть
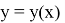
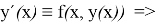
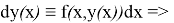
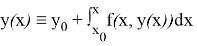
Следовательно, у=у(х) является решением (5).
Докажем обратное. Пусть у=у(х) является решением (5). Тогда,
дифференцируя
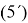
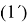
является решением (1), (2).
Эквивалентность (1), (2) и (5) доказана.
Будем в дальнейшем работать с (5).
Этап 2 : Найдём решение уравнения (5) с помощью последовательных приближений:
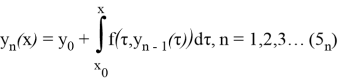
За нулевое приближение возьмём постоянное число
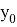
первое приближение
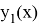
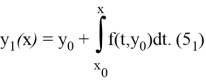
Так как функция под знаком интеграла известна, то
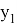
квадратурой; очевидно, при
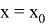
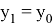
удовлетворяет начальному условию.
Мы ограничимся в формуле (
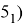
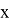
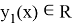
Следовательно, из (
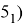
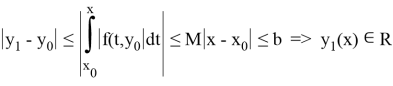
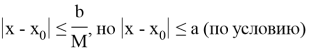
Следовательно,
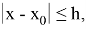
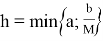
Продолжая и т. д. получим бесконечную функциональную последовательность
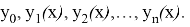
где каждая из функций
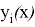
Этап 3:
Показывается, что существует предел последовательности
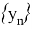
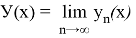
Этап 4: Показывается, что Y(x) есть решение (5)
Рассмотрим уравнение (
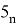
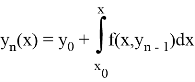
При n→∞ получим
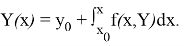
Этап 5: Доказывается, что найденное решение Y(x) есть единственное.
Это можно доказать методом от противного.
Литература:
- Матвеев Н. М. Методы интегрирования обыкновенных дифференциальных уравнений. Москва — 1967.
- Степанов В. В. Курс дифференциальных уравнений. М., 1958
- Танкиев И. А. Обыкновенные дифференциальные уравнения. Москва, ИЦ «Математика» 1997
- Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. М., 1969
- lionet J., Perez Carreras P. Barelled locally convex spaces//Math, studies. North Holland, 1987. V. 131.
- Шкаргт С. А. Нескольк результато о разрешимост обыкновенны линейны дифференциальны уравнени в локальн выпуклы пространства // Матем. сб. 1990. Т. 181, № 9. С. 1183–1195.







