Существует множество способов получения передаточной функции цифрового фильтра.
В данной статье рассматриваются следующие методы получения передаточной функции цифрового фильтра:
1) z -преобразование;
2) метод Тастина;
3) метод Цыпкина-Гольденберга.
Для того, чтобы построить цифровой фильтр, необходимо условиться с аналоговым прототипом. Рассмотрим обычный RLC-фильтр (рис. 1).
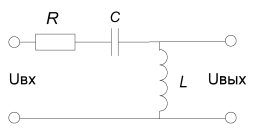
Рис. 1. Аналоговый прототип
Схема RLC -контура является электрической схемой, которая состоит из резистора, катушки индуктивности и конденсатора, соединенных последовательно или параллельно. Также RLC -контур является простейшей электрической схемой, способной совершать свободные колебания. [1, с. 5]
Это и будет аналоговый прототип получаемого цифрового фильтра.
Заданный аналоговый прототип имеет следующие параметры: сопротивление R =10 Ом , ёмкость С = 10 пФ и индуктивность L =100 мГн.
Прежде чем приступить к получению передаточной функции цифрового фильтра, необходимо посчитать операторную (передаточную) функцию заданного аналогового прототипа.
В нашем конкретном случае операторная функция K ( p ) представляет собой отношение напряжения на выходе к напряжению на входе:
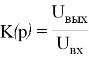
Известно, что в цепи протекает операторный ток
I
p
, а также операторные сопротивления конденсатора, индуктивности и резистора, соответственно равные
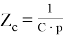
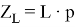
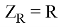
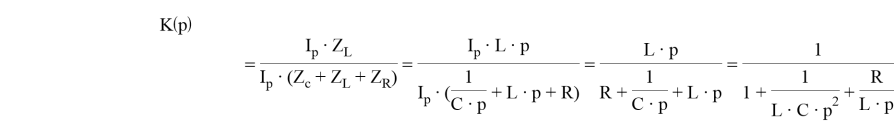
Таким образом, подставив исходные данные, получим, что
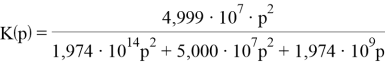
В z — области основной характеристикой цифрового фильтра является z — изображение импульсной характеристики h(n) .
Путем прямого z — преобразования импульсной характеристики мы получаем передаточную функцию H(z).
Передаточной функцией H(z) цифровогофильтра называется отношение z — изображения реакции на выходе цепи к z — изображению входного воздействия при нулевых начальных условиях.
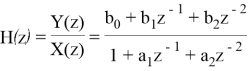
Один из самых простых методов нахождения дискретной передаточной функции основан на замене операторов непрерывного интегрирования их дискретными аналогами [2, с. 10].
Для этого передаточную функцию W ( p ) путём деления числителя и знаменателя на p k , где k -порядок системы, приводят к виду:
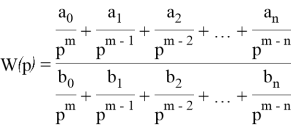
Заменяя интегратор
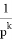
Переход от оператора непрерывного интегрирования к оператору дискретного интегрирования должен удовлетворять следующим условиям:
1) Переход в z-плоскость не должен сопровождаться потерей устойчивости;
2) Искажения частотных характеристик должны быть подвержены прогнозированию с целью их последующей коррекции, должна существовать возможность формирования требований к аналоговому прототипу;
3) Порядок передаточной функции цифрового фильтра не должен превышать порядка аналогового прототипа.
Последнее условие будет выполняться в случае, если порядок интегратора
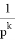
Для выполнения второго условия необходимо, чтобы мнимая ось p -плоскости отображалась в окрестность единичного радиуса при любых значения частоты. [3, с. 20]
Для этого должно выполняться одно из нескольких перечисленных условий:
1)A 0 =A 1 =A; B 0 =B 1 =B;
2)A 0 =-A 1 =A; B 0 =-B 1 =B;
3)A 0 =A 1 =A;B 0 =-B 1 =B;
4)A 0 =-A 1 =A; B 0 =B 1 =B.
Ниже представлены соответственно дискретные интеграторы первого и второго порядка.
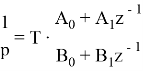
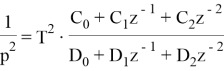
Далее применим билинейное z-преобразование, иначе известное как метод Тастина.
Билинейное z-преобразование с математической точки зрения представляет собой замену переменной.
В дискретной фильтрации это стандартный метод отображения переменной s (или аналоговой плоскости) в переменную z (то есть в дискретную плоскость). [4, с. 100]
Такое отображение преобразует аналоговые фильтры, рассчитанные классическими методами, в их дискретные эквиваленты.
Это простое конформное отображение s -плоскости в z -плоскость, свободное от некоторых недостатков и в то же время, сохраняющее удобную алгебраическую форму преобразования.
Метод билинейного преобразования обеспечивает более корректную замену операции дифференцирования дискретным эквивалентом.
Используется следующая замена:
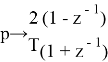
При билинейном преобразовании передаточная функция цифрового фильтра H ( z ) рассчитывается с помощью алгебраической подстановки.
Коэффициенты для интеграторов 1-го и 2-го порядка следующие:
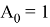
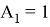
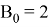
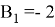
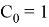
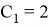
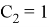

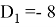
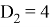
Передаточная функция H ( z ) для числа точек, равного 21, имеет следующий вид:
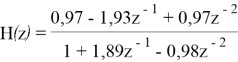
Теперь можем вывести разностное уравнение:
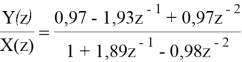
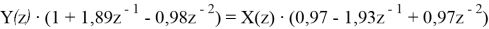
Таким образом, разностное уравнение примет следующий вид:
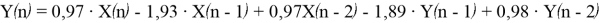
Исходя из данного уравнения, можем начертить структурную схему:
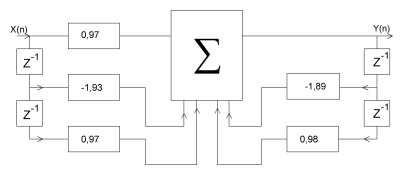
Рис. 2. Структурная схема ЛДС
Далее воспользуемся методом Цыпкина-Гольденберга.
Метод Цыпкина-Гольденберга не сильно отличается от билинейного преобразования, потому что это так же метод алгебраической подстановки, как и метод Тастина.
Единственное различие в значениях коэффициентах и, непосредственно, в самой подстановке.
Используется следующая замена для интегратора первого порядка:
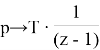
А коэффициенты его таковы:
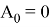
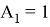
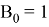

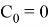
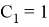
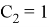
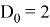

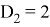
Таким образом получим следующую передаточную характеристику:
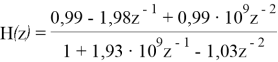
Теперь можем вывести разностное уравнение:
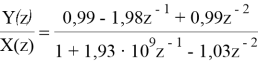
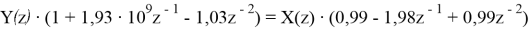
Для нормированного времени оно будет выглядеть так:

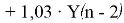
Структурная схема имеет следующий вид:
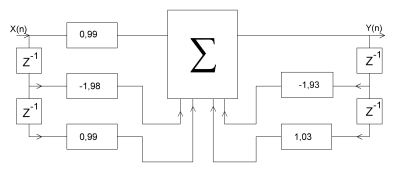
Рис. 3. Структурная схема ЛДС
Теперь применим стандартное z -преобразование.
Здесь переход от p к z иллюстрируется следующим образом:
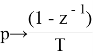
В таком случае, H ( z ) для 21 точки будет иметь такой вид:
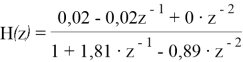
Теперь можем вывести разностное уравнение:
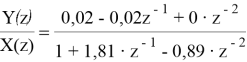
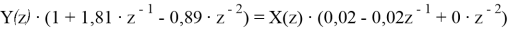
Таким образом, разностное уравнение примет следующий вид:
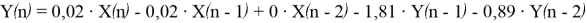
Структурная схема для данного метода будет иметь такой вид:
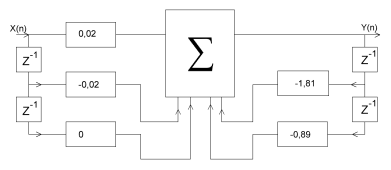
Рис. 4. Структурная схема ЛДС
Таким образом, в ходе сравнительного анализа были рассмотрены три метода z -преобразования для получения передаточной функции цифрового фильтра и построения разностного уравнения. Данная статья будет особенно актуальна при изучении студентами младших курсов специальности «Электроника и наноэлектроника» в качестве дополнительного материала к дисциплине «Цифровая обработка сигналов».
Литература:
- Солонина А. И. Линейные дискретные системы: учеб. пособие / СПбГУТ. СПб, 2005.- 76 с
- Глинченко А. С. Цифровая обработка сигналов: курс лекций / Красноярск: ИПК СФУ, — 2008. — 242 с.
- Яшин Е. Н. Дискретные системы: методические указания / сост.: Муромцев Д. Ю., Яшин Е. Н.. — Тамбов: Изд. тамб. гос. техн. ун-та, 2009. — 32 с.
- Токхейм Р. Основы цифровой электроники: Пер. с анг. — М.: Мир, 1988. — 392 с.







