В статье рассматриваются только конечные группы. Установлено влияние свойств класса групп
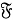
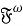
Ключевые слова: конечная группа; класс групп; подгрупповой функтор.
В последнее время в алгебре в рамках теории конечных групп активно развивается теория подгрупповых функторов, позволяющая устанавливать связь между свойствами классов групп и внутренним строением конечных групп (см., например, [2]). Большую роль в теории конечных групп играет понятие максимальной подгруппы группы. С развитием теории классов групп стали изучаться максимальные подгруппы в группах, связанные с рассматриваемыми классами. Центральное место среди них заняли
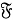
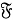
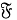
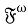
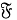
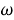
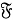
Цель данной работы состоит в исследовании свойств подгрупповых функторов в зависимости от свойств данного класса конечных групп. Установлено влияние свойства
Q
-1
-замкнутости класса групп
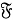
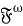
Запись
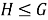
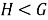
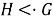
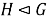
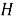
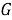
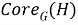
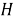
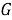
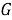
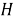
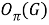
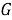
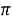
Отображение
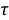
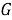
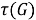
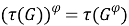
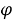
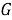
Совокупность групп
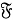
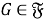
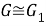
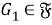
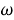
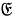
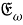
Пусть
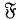
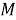
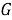
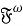
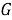
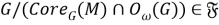
Класс групп
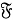
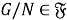
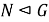
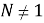
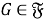
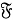
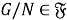
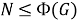
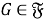
Исследуем влияние свойства
Q
-1
-
замкнутости класса групп
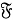
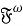
Лемма 1. Пусть
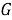
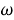
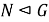
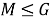
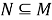
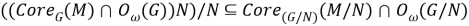
Доказательство
. Пусть
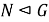
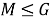
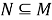
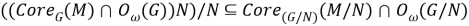
Введем следующие обозначения: пусть
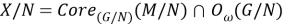
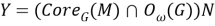
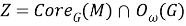
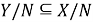
Так как
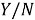

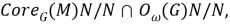
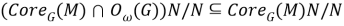
Поскольку
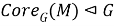
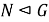
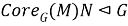
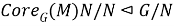
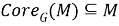
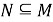
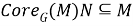
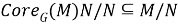
Так как, согласно определению ядра подгруппы в группе,
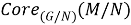
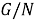
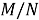
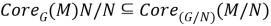
Из (3) и (6) получаем, что
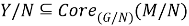
Далее, по определению операции пересечения, имеем
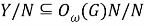
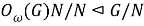
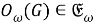
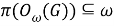
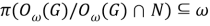
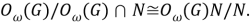
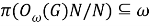
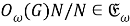
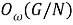
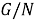
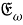
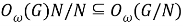
Из (8) и (9) получаем, что
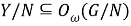
Из (7) и (10) следует, что включение (2) верно, и, значит, включение (1) справедливо. Таким образом,
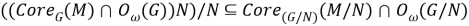
Лемма доказана.
Теорема 1. Пусть
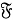
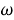
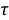
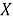
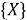
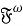
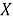
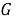
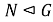
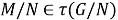
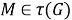
Доказательство.
Пусть
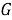
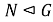
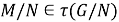
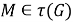
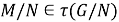
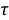
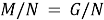
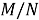
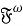
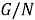
Рассмотрим каждый из случаев.
1) Пусть
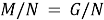
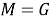
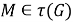
2) Пусть
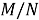
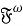
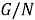

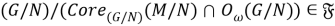
Из (1), ввиду леммы 3.17 [3, с. 112], получаем, что

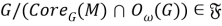
пусть
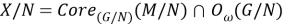
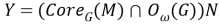
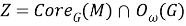
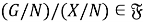
Из леммы 1 следует, что
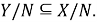
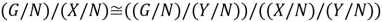
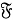
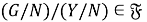
Поскольку
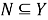
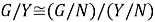
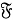
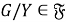
Из равенства

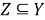
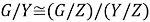
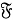
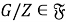
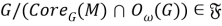
Таким образом, из (3) и (7) получаем, что
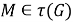
Теорема доказана.
Литература:
- Каморников С.Ф., Селькин М.В. О влиянии максимальных подгрупп примарного индекса на строение конечной группы // Известия высшего учебного заведения. Математика. 1995. № 6. − С. 24−28.
- Каморников С.Ф., Селькин М.В. Подгрупповые функторы и классы конечных групп. – Минск: Беларуская навука, 2003. – 254 c.
- Монахов В.С. Введение в теорию конечных групп и их классов: учебное пособие. – Минск: Вышэйшая школа, 2006. – 207 с.
-
Селькин М.В. Конечные группы с заданными
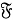
- Селькин М.В. Максимальные подгруппы в теории классов конечных групп. − Минск: Беларусская наука, 1997. – 145 с.
- Селькин М.В. О влиянии максимальных подгрупп на формационное строение конечных групп // Конечные группы. – Минск: Наука и техника, 1975. – С. 151–163.
- Селькин М.В. О максимальных подгруппах конечных групп // ДАН БССР. 1974. Т. 18, № 11. − С. 969−972.
- Скиба А.Н. О решетке подгрупповых функторов // Вопросы алгебры. – Гомель, 1996. Выпуск 10. – С. 177−186.
- Шеметков Л.А. Два направления в развитии непростых конечных групп // Успехи математических наук. 1975. Т. 30, № 2. − С. 179−198.
- Шеметков Л.А. Формации конечных групп. – Москва: Наука, 1978. – 272 с.
- Ballester-Bolinches A. Maximal subgroups and formations // J. Pure Appl. Algebra. 1989. V. 62. − P. 223−232.
- Doerk K., Нawkes T. Finite soluble groups. − Berlin − New York: Walter de Gruyter, 1992. – 893 p.







