Keywords : infinite series, integral, improper integral, integration by parts, infinitely decreasing geometric progression, differentiate, Riemann zeta function.
In our daily college or school life, we can sometimes face number series as: 1+2+3+…+n. Some of us are able to calculate this kind of number series. What if amount of elements of number series are infinitive? In these cases, it is impossible to calculate value of sum of elements in number series when
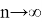
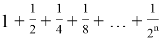
First example:
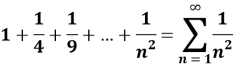
Lemma 1:
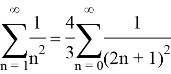
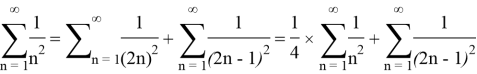
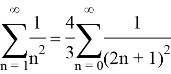
Lemma 1 was proved.
Lemma 2:
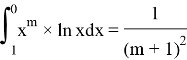
To make our life easier we can use integration by parts:
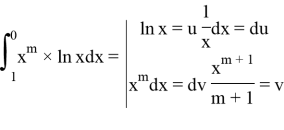
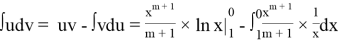
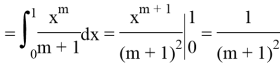
Lemma 2 was proved.
We express Lemma 1 in terms of Lemma 2:
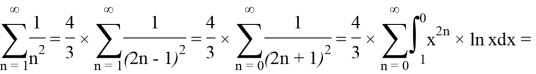
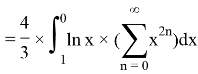
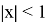
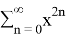
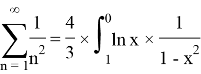
We can develop and change our natural logarithms by using limits into:
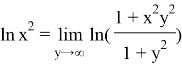
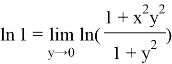
We can also rewrite
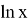
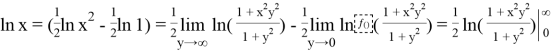
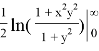
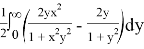
It is time to replace natural logarithm to our derived integral above and put all of them to the Lemma 1:
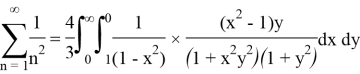
It is obvious that we can cancel
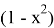
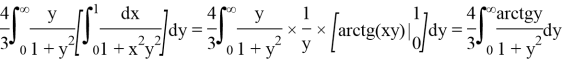
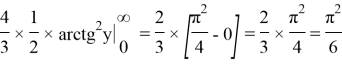
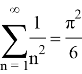
Second example:
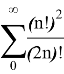
Lemma 1:
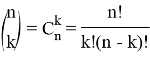
By using combinatorics, we can rewrite this expression
(
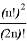
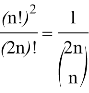
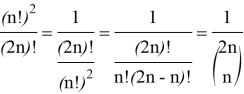
Lemma 1 was proved.
Lemma 2:
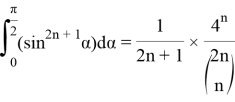
Below we will prove mathematical induction:
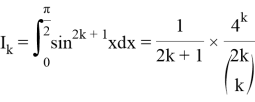
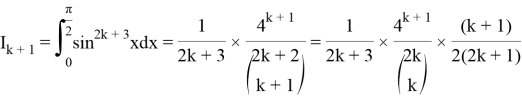
To make our life easier we can use integration by parts:
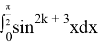
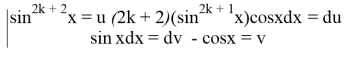
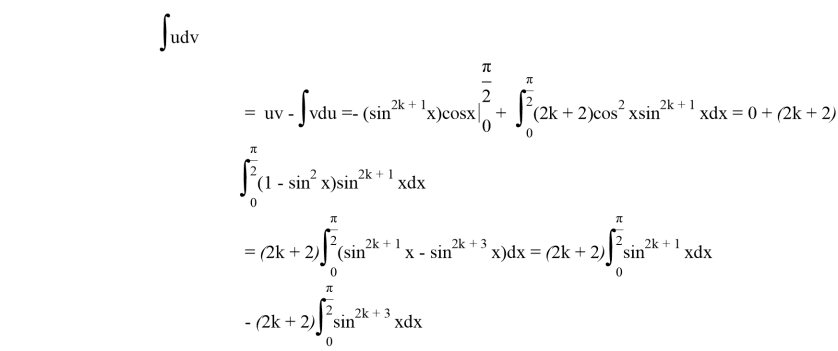
Above we can replace
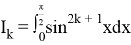
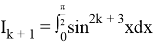
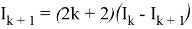
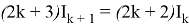
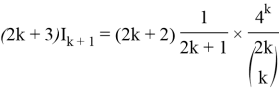
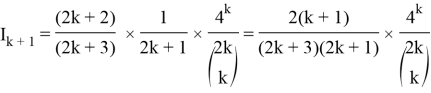
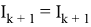
Lemma 3:
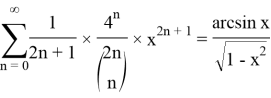
We use Lemma 2:
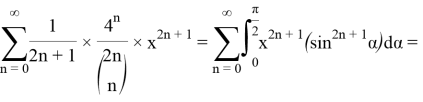
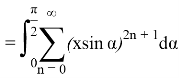
At
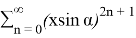
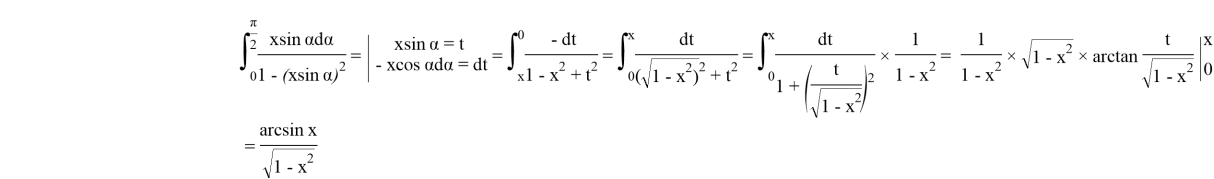
Lemma 3 was proved.
We should take a derivative Lemma 3 with respect to X
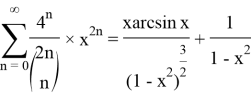
As written above at
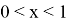

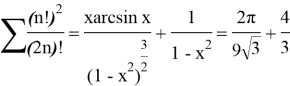
Third example:
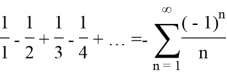
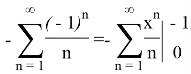
Now we have to differentiate this expression with respect to x and write in integral form:
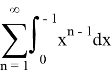
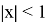
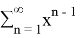
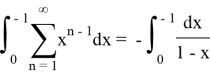
After integration we get an answer:
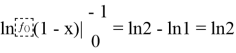
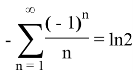
Conclusion
Over the examples considered, we wanted to show that the sum of infinite series is not always indefinable, and even if it is possible, it is not easy. For example, we showed that the Riemann Zeta function about n equals 2 is definable, but if n were an odd number, then we could not determine. Finally, we want to say that infinity was and remains a mystery for the world of science.
References:
- Ter-Krikorov A. M. Mathematical Analysis Course/ A. M. Ter-Krikorov, M. I. Shabunin—6. — Moscow:Binom 2013–672p.
- Ilyin, V. A. Fundamentals of Mathematical Analysis/ V. A. Ilyin, E. G. Poznyak —7. —Moscow:Fizmatlit, 2001–645p.







