Векторно-координатный метод решения задач является одним из самых мощных способов, использование которого позволяет решать многие физические, технические и математические задачи. Привлекательность данного метода обусловлена его алгоритмичностью — возможностью построения систем последовательных операций, описывающих порядок действий для решения той или иной задачи. В данной статье доказываются основные свойства параллелограмма векторно-координатным методом.
Ключевые слова: векторно-координатный метод, геометрическая задача, свойства параллелограмма.
Решение геометрических задач, как правило, требует широкого пространственного мышления, наглядного представления сложных конфигураций, грамотной корреляции богатого математического знания. Еще В. Г. Болтянский отмечал: «Трудность решения геометрических задач заключается не только и не столько в том, что надо выполнить несколько операций; основная трудность состоит в отыскании необходимой последовательности действий , выполнения которых ведет к решению задачи» [2, с. 28].
Данное обстоятельство, сопровождающееся нехваткой времени, необходимого для решения той или иной задачи, вызывают трудности, провоцирующие нас к поиску наиболее оптимального метода решения геометрических задач и его использовании на технологическом уровне.
Векторно-координатный метод используется в различных областях науки и техники, общественной жизни. Данный метод лежит в основе механики, геодезии, экономики, астрономии, географии, медицине. Особая его роль отводится в математике, в частности, при решении геометрических задач. Так данный метод позволяет сопоставить геометрическим объектам (фигурам, отрезкам, векторам), соответствующие им алгебраические соотношения, в результате чего появляются возможности более рационально решать многие задачи, строить доказательства [4].
В данной статье приводятся доказательства основных свойств параллелограмма при помощи векторно-координатного метода.
Основная часть
Для обеспечения овладением первичными навыками использования векторно-координатного метода на практическом уровне рассмотрим основные свойства параллелограмма, установим их истинность при помощи данного метода. Анализ учебников геометрии (Атанасян Л. С. [1], Погорелов А. В. [3], Смирнова, И.М. [5], Шарыгин И.Ф [6]) позволил синтезировать основные свойства параллелограмма.
Свойство 1. Противоположные стороны параллелограмма равны.
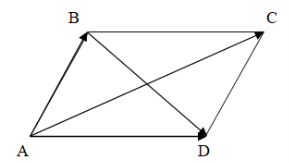

Дано
:
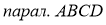
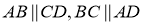
Доказать
:
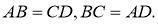
Доказательство:
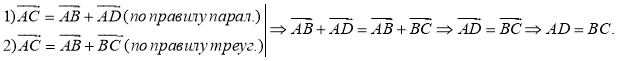
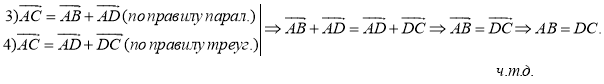
Свойство 2. Противоположные углы параллелограмма равны.
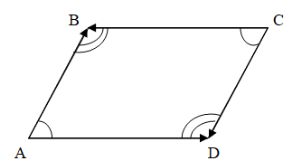
Дано
:
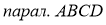
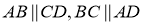
Доказать
:
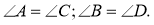
Доказательство:
Воспользуемся скалярным произведением векторов
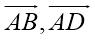
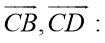
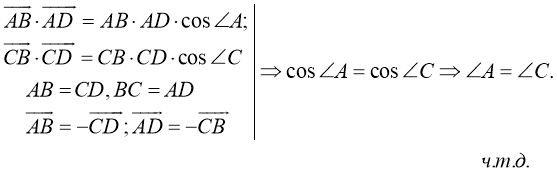
Свойство 3. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам.
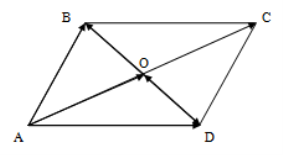
Дано:
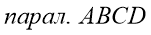
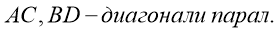
Доказать
:
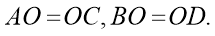
Доказательство:
- По правилу треугольника получаем:
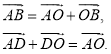
- Просуммируем первое и второе равенство:
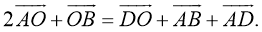
- По правилу параллелограмма получаем:
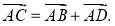
-
Пусть
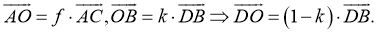
- Подставим полученные результаты в пункт 2:
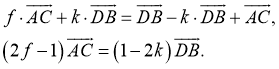
-
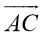
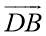
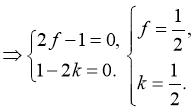
-
Таким образом,
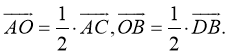
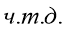
Свойство 4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
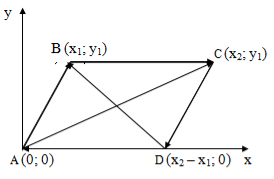
Дано:
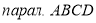
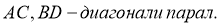
Доказать :
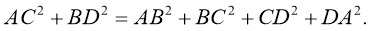
Доказательство:
-
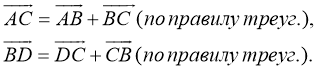
- Возведем левые и правые части равенств и соответственно их просуммируем:
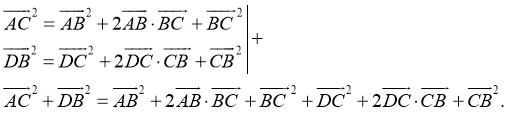
- Воспользуемся скалярным произведением:
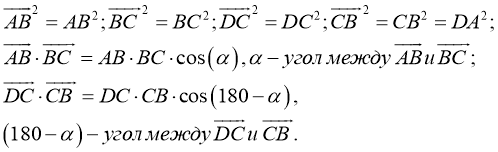
Преобразуем последнее равенство, получим:
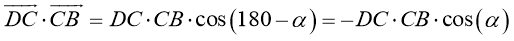
- Принимая во внимание свойство 1, получим:
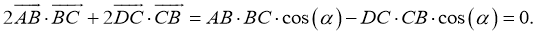
-
Таким образом,
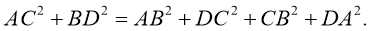
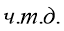
Свойство 5. Биссектрисы противоположных углов параллелограмма всегда параллельны.
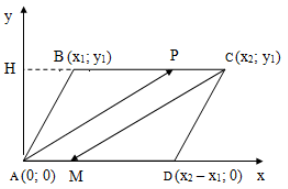
Дано:
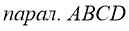
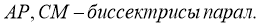
Доказать:
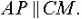
Доказательство: Пусть
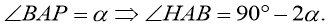
Определим координаты векторов
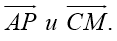
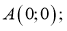
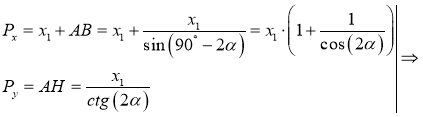
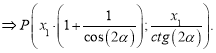
Таким образом,
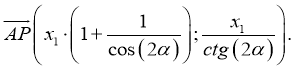
2.
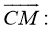
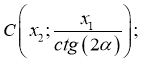
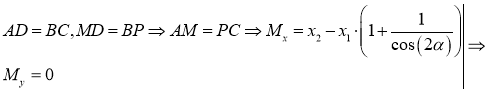
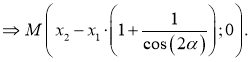
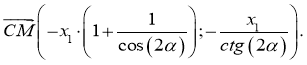
-
Определим косинус угла между векторами
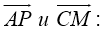
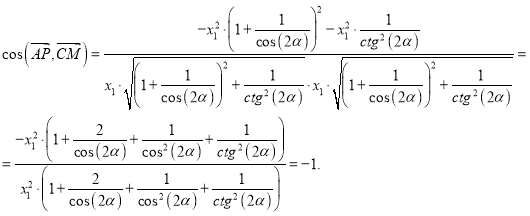
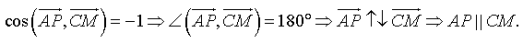
ч. т. д.
Свойство 6. Биссектрисы односторонних углов параллелограмма взаимно перпендикулярны.
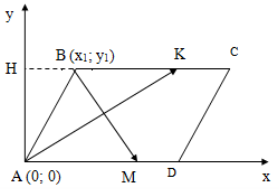
Дано:
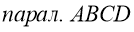
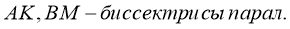
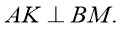
Доказательство
: Пусть
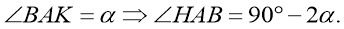
Определим координаты векторов
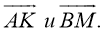
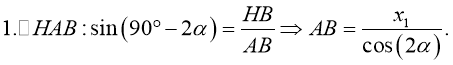
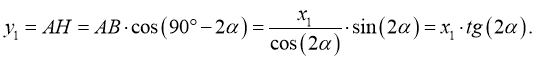
-
Определим координаты векторов
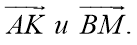
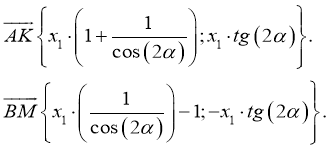
-
Определим скалярное произведение векторов
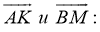

-
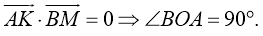
Заключение
Векторно-координатный метод соединяет в себе метод координат и векторный метод и позволяет при помощи необходимых формул найти удобный подход к решению сложных геометрических задач.
Особо важно подчеркнуть прикладной характер изучения векторно-координатного метода как отправной точки подготовки к ЕГЭ по профильной математике, что придает ему значимость и определяет перспективы настоящего исследования.
Литература:
- Атанасян Л. C. Геометрия, 7–9: учеб. для общеобразоват. учреждений / JI. C. Атанасян и др.. — 12-е изд. — М.: Просвещение, 2002. — 384 с.
- Болтянский В. Г., Савин А. П. Беседы по математике. Кн. 1. Дискретные объекты. — М.: ФИМА, МЦНМО, 2002. — 368 с.
- Погорелов А. В. Геометрия. 10–11 классы: учебник для общеобразовательных учреждений / А. В. Погорелов. — 9-е изд. — М.: Просвещение, 2009.- 175 с.
- Потоскуев Е. В. Векторы и координаты как аппарат решения геометрических задач. 10–11 класс: Элективные курс / Е. В. Потоскуев. — М.: Издательство «Дрофа», 2008. — 176 с.
- Смирнова И. М. Геометрия. 7–9 классы: учеб. для общеобразоват. учреждений / И. М. Смирнова, В. А. Смирнов. 3-е изд., стер. — М.: Мнемозина, 2008. — 376 с.
- Шарыгин И. Ф. Геометрия. 7–9 кл.: учеб. для общеобразоват. учеб. заведений / И. Ф. Шарыгин. 5-е изд. стереотип. — М.: Дрофа, 2001. — 368 с.