1. Введение
В связи с развитием таких направлений науки и техники как механика, теплотехника, математическая химия, самолетостроение, наноэлектроника, наноматериалы, нанооборудование и нанометрология, нанобиотехнологии, основанные на достижениях молекулярной биологии и генной инженерии, гелио- и ядерная энергетика, возникла потребность не только вычисления приближенных решений различных задач и гарантированных оценок их близости к точным решениям, но и попытка обосновать целостное видение процесса современного развития глобальной экономики в единстве технологического, макроэкономического и управленческого аспектов. Исходя из современной теории долгосрочного технико-экономического развития как процесса последовательной смены технологических укладов, интерес к интервальному анализу и вопросам двухсторонних оценок как к возможным средствам оценки погрешностей аналитическо-приближенных решений и раскрываются глубинные причины, связанные с замещением доминирующих технологических укладов, в последнее время нарастает. В частности, интервальный анализ нанотехнологии появился сравнительно недавно как метод автоматического контроля, распространение революционизирует традиционные и порождает новые направления экономического роста, повышая экономическую эффективность производства и расширяя возможности потребления, создавая новые сферы экономической деятельности. Впоследствии он превратится в один из разделов формирования нового технологического уклада, исследуется процесс их распространений в мировой экономике, обосновываются рекомендации по политике опережающего развития последней на основе своевременного становления ядра нового технологического уклада, составляющими которого являются рост ядерной энергетики и потребления природного газа.
В процессе распространения интервального анализа и вопросов двухсторонних оценок ожидается, что рост ядерной энергетики и потребления природного газа будет дополнен расширением сферы использования водорода в качестве экологически чистого энергоносителя, существенно расширится применение возобновляемых источников энергии, прежде всего солнечной энергии. Производственная сфера перейдет к экологически чистым и безотходным технологиям. Обычно такие прикладные задачи имеет нестабильные решение
Основная идея интервального анализа состоит в замене точных информационных модельных операции на интервальные модельные операции и функции, преобразующими интервалы, содержащие эти информации. Ценность интервальных решений заключается в том, что они содержат точную информацию о решении исходных задач.
В значительной мере это вопросы риторические, так как в течение последних десятилетий накоплено достаточно много примеров плодотворного применения интервальных методов к задачам, которые до сих пор никак иначе не решались или решались неудовлетворительно. Таковы, в частности, задачи доказательной глобальной оптимизации и доказательного глобального решения уравнений и систем уравнений [1–5]. Кроме того, интервальный анализ предоставляет нам новый язык для описания задач с ограниченными неопределенностями и неоднозначностями в данных [6], язык удобный и весьма выразительный, который существенно обогащает арсенал методов математического моделирования окружающей нас действительности. В частности, система линейных алгебраических уравнений (СЛАУ) используется при математическом моделировании объектов различной природы: физических, химических и социально-экономических процессов, процессов управления.
В ходе качественного анализа и/или использования математических моделей необходимо решать различные системы линейных алгебраических уравнений. Например, в задачах строительной механики [7] при определении усилий в стержнях ферм применяют систему вида:
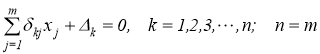
где
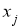
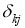
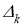
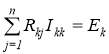
где R kj — сопротивление смежных ветвей между k -м и j -м контурами, E k — контурная ЭДС k -го контура, I kk – контурный ток в k -м контуре. В общем виде эти системы представим так:
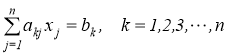
или в матричном виде:
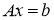
Системы уравнения (1), (2) и (3), (4) имеют важную особенность. Все входящие в эти системы параметры и неизвестные величины имеют реальный физический смысл и, в силу этого, их значения могут быть получены с некоторой погрешностью. В зависимости от конкретного физического смысла задачи эти погрешности могут быть заранее известными, а в некоторых случаях их определение невозможно. Таким образом, можно утверждать, что все эти величины известны с некоторой неустранимой неопределённостью. В соответствии с [9] различают неопределенность типа А, которую оценивают статистическими методами и неопределенность типа b , которую оценивают нестатистическими методами. При этом предлагается два метода оценивания неопределенностей А и b . Для неопределенности типа А это использование известных статистических оценок среднеарифметического значения и среднеквадратического отклонения, используя результаты измерений и опираясь, в основном, на нормальный закон распределения полученных величин. Для неопределенности типа b это использование априорной нестатистической информации, опираясь, в основном, на равномерный закон распределения возможных значений величин в определенных границах. Таким образом, возникает задача получения решения СЛАУ с учётом этой неопределённости.
Пусть дана система линейных алгебраических уравнений (4), где A –матрица размерности n*n , x– искомый вектор, b –известный вектор. Эта система может быть однозначно разрешимой, неразрешимой и вырожденной (иметь бесконечно много решений).
При численном решении таких СЛАУ точными методами возникает несколько источников неточности решения. Одним из них является необходимость округления чисел в процессе вычисления. Второй источник появляется в условиях, когда СЛАУ в процессе решения практической задачи, так что элементы матрицы коэффициентов, так же как и свободные члены, известны лишь приближенно, с некоторой степенью точности. Неточность самих исходных данных порождает ошибки в решении, таких как изменение коэффициентов системы и свободных членов в пределах заданной точности влечет за собой изменение решения.
Метод нахождения нормального решения системы (4), устойчивого к малым возмущениям правой части
b
и матрицы
A,
основанный на методе регуляризации рассматривался в работе А. Н. Тихонова [10, 11]. Выходные данные системы задаются с некоторой погрешностью, то есть вместо
b
и
A
задаются
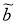
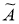
На практике необходимо решать плохо обусловленные и даже вырожденные СЛАУ, неустойчивых к возмущениям и погрешностям входных данных. Основная сложность решения плохо обусловленные и вырожденные СЛАУ — недостаточная информативность измерений, приводящая к математической неоднозначности в определении точных решении. В связи с этим возникает проблема неединственности решения СЛАУ, сформулированная в задачах. При моделировании принято использовать средние значения параметров, что не позволяет предусмотреть все варианты режима функционирования СЛАУ, которые могут возникать в процессе ее эксплуатации. На самом деле элементы матрицы и правой части СЛАУ известны в некоторых интервалах возможных значений. В таком случае под решением СЛАУ определения точных решении целесообразно подразумевать некоторую область, вариация элементы матрица и правой части, внутри которой сохраняет требуемое качество описания измерений. Другая постановка расчета областей неопределенности погрешности измерений. Необходимо только знание величины предельно допустимой погрешности эксперимента.
В свете вышесказанного представляется перспективным альтернативное направление развития нечеткой плохо обусловленные и вырожденные СЛАУ, в котором элементы матрицы и правой части принадлежности в некоторых интервалах возможных значений.
2. Прогноз выпуска продукции по запасам сырья
Системы с интервальной неопределённостью возникают во многих математических и прикладных областях, при решении экономических задач, при вычислении значений собственных функций, в распознавании образов для анализа зашумленных изображений, в физических задачах, как линеаризованные постановки нелинейных задач, в химии при анализе состава смесей хемометрическими методами и многих других. Подробно будут рассмотрены примеры из области экономики.
Малое предприятие выпускает два вида продукции, используя два типа ресурсов. Сведения о расходе сырья для каждого вида продукции и запасе сырья каждого типа представлены в таблице. Требуется определить план выпуска каждого вида продукции при условии использования всего имеющегося в запасе сырья.
|
Тип сырья |
Расход сырья по видам продукции, ед./изд. |
Запас сырья, ед. |
|
|
П 1 |
П 2 |
||
|
С 1 |
1 |
1.4 |
38.2 |
|
С 2 |
0.99 |
1.386 |
37.818 |
Принятые обозначения:
А — матрица норм затрат ресурсов, В — запасы ресурсов, С — прибыль на единицу продукции.
А =
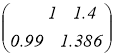
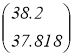
Решение: например, пусть выпускает в количестве x 1 -сорочки (пальто), x 2 -брюки (пуховики). Тогда исходя из таблицы, с расходом материала каждого вида, получаем систему:
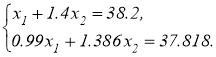
Данная система представляет собой два линейных уравнения, с двумя неизвестными. Такая система является математической моделью. И составление такой системы является лишь первым шагом в исследовании данного процесса. Второй шаг заключается в том, чтобы найти решение, а именно совокупность данных значений неизвестных: x 1 , x 2 , которые давали бы верное решение всем уравнениям. Понятно, для того, что решить данную экономическую задачу необходимо разобраться с основными понятиями, которые характерны для систем линейных уравнений; необходимо изучить свойства математических объектов и потом на их основе уже выбрать метод решения.
Прогнозирования выпуска продукции по запасам сырья требуется:
1) составить экономико-математическую модель задачи;
2) определить план выпуска изделий, обеспечивающий получение максимальной прибыли;
3) найти стабильное оптимальное решение;
4) определить интервал стабильности оценки ресурса;
5) проанализировать, как изменится максимальная прибыль малого предприятия в результате уменьшения запасов второго ресурса на определенное количество единиц.
Приведем пример простой СЛАУ, являющейся вырожденной, для которой традиционные методы решения некорректных задач, таких как, например, нормальное псевдорешение по А. Н. Тихонову и М. М. Лаврентьеву имеет недостатки. Нормальное псевдорешение СЛАУ есть ( x 1 , x 2 )=(13,18) , однако в случае минимальных колебаний значений коэффициентов, например,
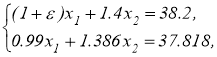
>0, система имеет единственное точное решение ( x 1 , x 2 )=(0,27.285714) , и сходимости при ε → 0 к нормальному псевдорешению нет.
Если же принять изначально интервальную постановку, то есть допустить колебание элемента a 11 в закрытом интервале [1,1 + ε], то вычислив решение интервальной СЛАУ, мы получим точку ( x 1 , x 2 )=(0,27.285714) , которая является точным решением для любой системы из семейства СЛАУ описываемых соотношениями (5а), то есть является устойчивым к колебаниям коэффициентов в рамках заданных интервалов, тем самым можно устранить влияние возможных колебаний коэффициентов правой части уравнения на результат. В данной работе предлагается способ поиска решения подобных некорректных задач исходя из следующего определения
Определение . Псевдорешениями интервальной СЛАУ (4) назовем точки допускового множества системы
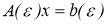
с расширенной элементы матрицы A()={ [ a kj -p, a kj +q] } ( k,j =1,2,…,n) и правой частью b() = [︀b−p, b + q]︀, где p, q — константные положительные векторы, определяющие характер расширения исходя из содержательного смысла задачи, ≥ 0 — параметр, отвечающий за величину расширения.
Но несмотря на удобства предоставляемых прикладных задач, все рассмотренные примеры демонстрируют, что не овладев предметной областью и фундаментальными математическими понятиями, решить их невозможно. Моделирование является одним из методов научного познания. Математическая модель позволяет экономить материальные ресурсы и предоставляет возможность изучать поведение системы в заданных экспериментатором условиях.
3. Постановка задачи
В рамках данной работы будут рассмотрены только экономически реализуемые системы, то есть такие, численные значения характеристик которых отличны от нуля. Выделим следующие варианты постановки задач: прямую и обратную. Прямая постановка задачи предполагает следующую формулировку. Определить с точностью до заданного интервала неопределённости значение вектора x при условии задания матрицы А и вектора b с такой же мерой неопределённости. Обратная постановка задачи предполагает, что заданы векторы x и b, требуется определить матрицу А при сохранении тех же тошнотных характеристик. Таким образом, решение прямой задачи можно считать задачей анализа системы, решение обратной задачи — задачей её синтеза.
Рассмотрим для определенности вырожденные системы (4). В этом случае речь может идти лишь о нахождении их нормального решения.
Пусть
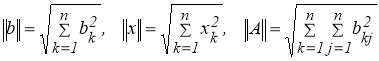
Предположим, что вектор
b
мы знаем в какой-то степени неопределенно (то есть нам известно лишь некоторое приближение
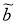
Пусть
x
*
-нормальное решение системы (4), и
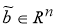
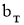
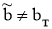
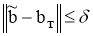
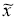
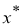
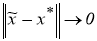
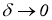
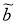
4 . Класс возможных приближенных решений
Пусть системы уравнение (4) имеет нормальное решение
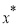
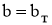
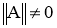
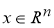
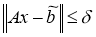
Класс
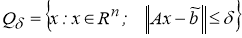
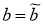
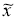
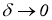
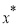
Согласно [13], в качестве приближения к
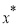
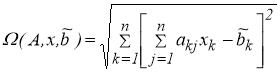
на множестве
Q
(
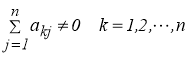
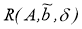
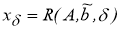
Нетрудно убедиться, что существует один и только один вектор
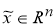
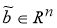
5. Единственности нормального решения
Поскольку (7) неотрицательный функционал, то существуют его точная нижняя грань на множестве Q
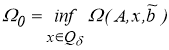
и минимизирующая последовательность
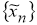
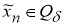
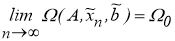
Не ограничивая общности, можно полагать, что для всякого
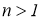
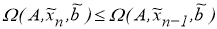
Следовательно, для любого
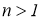
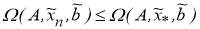
Таким образом, элементы последовательности
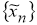
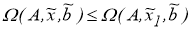
при любых фиксированных
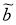
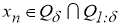
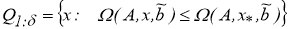
замкнутое ограниченное множество в
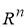
По теореме Больцано-Вейерштрасса из последовательности
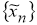
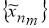
Пусть
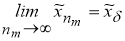
В силу замкнутости множества
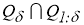
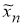
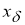
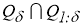
Так как
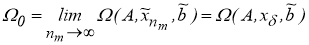
то функционал (3) достигает минимума на множестве
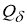
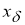
Таким образом, элемент
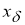
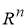
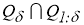
Пусть задана последовательность
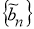
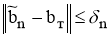
где
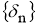
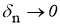
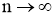
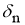
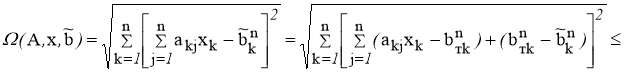
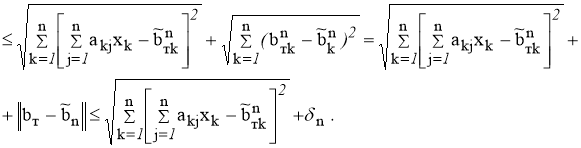
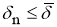
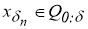
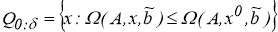
С другой стороны, для всякого
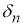
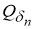
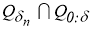
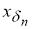
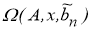
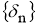
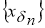
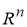
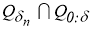
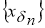
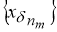
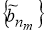
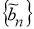
Пусть
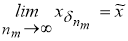
Так как
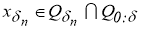
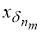
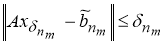
Переходя в нем к пределу при
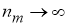
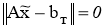
Следовательно,
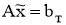
В силу единственности нормального решения системы уравнений (4) с правой частью
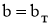
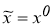
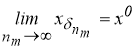
Отсюда следует, что для любой последовательности
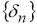
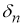
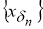
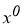
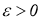
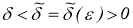
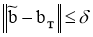
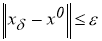
Теорема 1.
Вектор
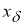
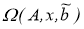
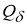
1) он определен для всякого
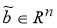
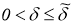
2)
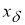
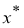
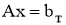
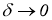
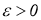
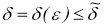
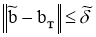
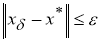
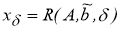
3) он является регуляризирующим для системы уравнения (1).
6. Основные результаты
Пусть
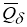
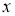
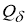
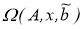
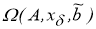
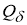
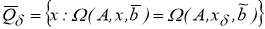
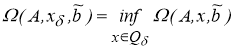
Предположим, что для
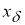
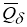
1)
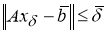
2)
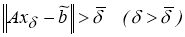
В первом случае решением вариационной задачи на минимум функционала
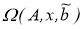
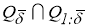
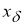
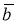
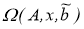
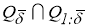
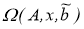
Допустим, что
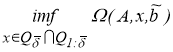
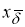
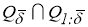
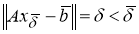
По условию,
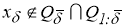
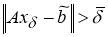
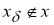
С другой стороны, если
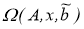
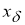
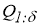
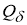
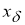
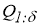
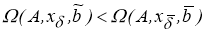
Так как элемент
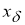
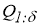
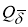
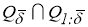
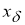
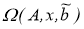
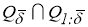
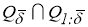
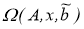
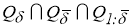
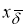
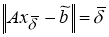
Тогда задачу нахождения вектора
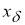
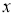
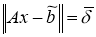
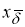
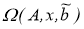
Эту задачу можно решить методом Лагранже, то есть в качестве
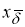
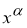
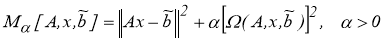
с параметром α, определяемым по невязке или по отношению двух норм (см. [11]).
7. Минимизации функционал типа А. Н. Тихонова
Рассмотрим квадратичный функционал (9), где
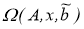
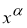
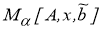
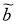
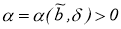
Вектор
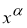
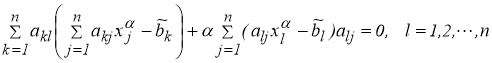
получающихся из условий минимума функционала
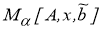
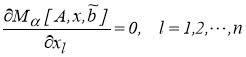
Вектор
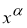
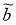
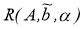
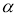
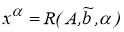
Если
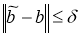
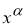
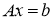
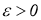
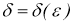
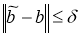
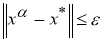
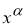
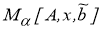
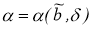
Отсюда следует, что при любом
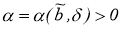
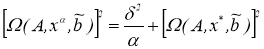
Действительно,
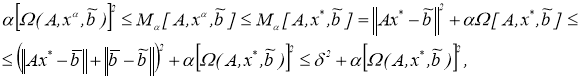
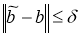
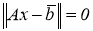
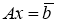
Таким образом, для любого
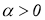
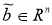
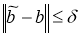
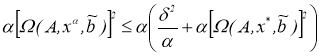
Пусть
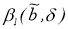
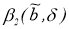
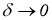
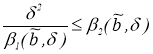
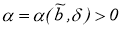
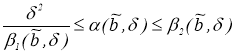
будем иметь
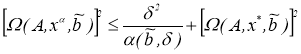
где
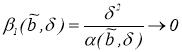
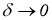
Докажем теперь, что для любого
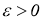
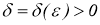
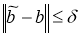
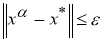
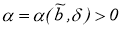
Для этого достаточно доказать, что из любой последовательности
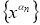
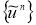
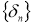
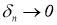
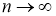
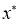
Пусть
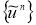
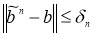
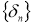
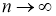
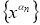
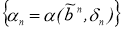
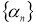
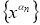
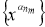
Пусть
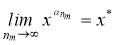
В этом случае, для всякого
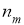
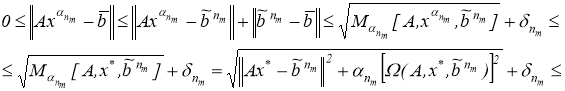
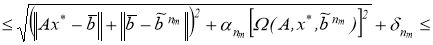
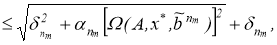
так как
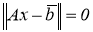
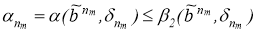
получим
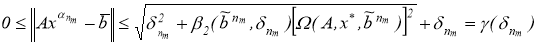
где
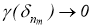
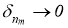
Переходя в нем к пределу при
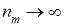
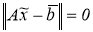
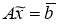
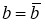
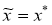
Таким образом,
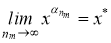
Отсюда следует, что из любой последовательности
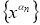
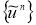
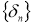
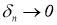
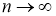
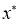
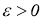
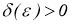
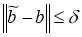
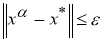
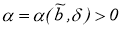
Теорема 2.
Пусть
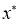
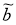
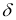
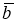
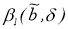
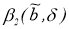
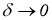
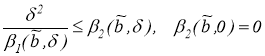
Тогда для любой положительной функции
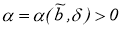
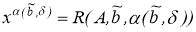
сходятся к нормальному решению
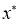
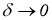
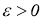
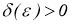
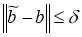
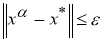
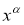
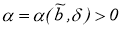
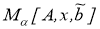
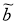
8. Вычислительный эксперимент
При разработке численных алгоритмов наиболее естественно использовать метод регуляризации, минимизации функционал (7) и (9), оставляя в СЛАУ конечное число уравнений и конечное число неизвестных.
Исследуем поведение решение СЛАУ с двумя уравнениями и двумя неизвестными вида (5). График решений
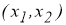
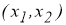
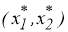
На рис. 1 (а, б) представлены решения
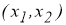
а)
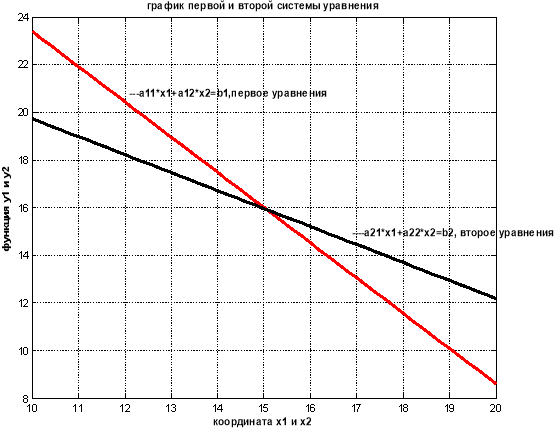
б)
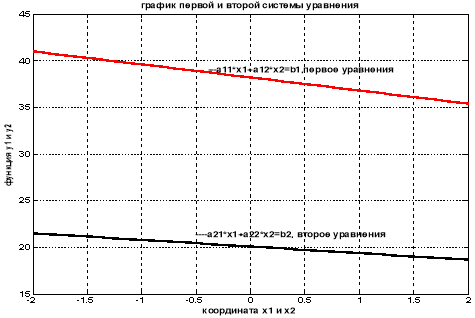
Рис.1. График поведения системы (5)
Из рис.1 видно, что графики системы точки пересечения не имеет, то есть прямые линии лежат параллельно. Если график системы уравнений точки пересечение не имеет, то она вырожденная.
Литература:
- 1.Добронец Б. С. Интервальная математика: Учеб. Пособие /Б. С. Добронец // -Красноярск: Красноярский государственный университет. -2004. -216 с.
- Shary, S. P. A new technique in systems analysis under interval uncertainty and ambiguity / S. P. Shary // Reliable Computing. — 2002. — Vol. 8, no. 5. —P. 321–418.
- Panyukov, A. V. Computing best possible pseudo-solutions to interval linear systems of equations / A. V. Panyukov, V. A. Golodov // Reliable Computing. –2013. –Vol. 19. –P. 215–228.
- Шарый, С. П. Конечномерный интервальный анализ / С. П. Шарый. — Новосибирск, «XYZ», 2013. —С. 285.
- Алтунин А. Е., Семухин М. В. Модели и алгоритмы принятия решений в нечетких условиях: Монография. -Тюмень: Издательство Тюменского государственного университета, 2000. 352 с.
- 6.Жолен Л., Кифер М., Дидри О., Вальтер Э. Прикладной интервальный анализ. -М.-Ижевск: Институт компьютерных исследований. -2005. –468 с.
- Дарков А. В. Строительная механика / А. В. Дарков, Н. Н. Шапошников. — М.: Высш. шк., 1986. — 607 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи./ Л. А. Бессонов. — М.: Высш. шк., 1996. — 626 с.
- Захаров И. П. Теория неопределённости в измерениях. / И. П. Захаров, В. Д. Кукуш. — Харков:Консум. –2002. — 256 с.
- Тихонов А. Н. О некорректных задачах линейной алгебры и устойчивом методе их решения. //ДАН СССР. -1965.-Т.163, № 6.
- Тихонов А. Н. Об устойчивости алгоритмов для решения вырожденных систем линейных алгебраических уравнений. // ЖВМ и МФ. -1965. –Т.5, № 4
- Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. –М.: Наука. -1986. — 288 с.
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. -М.: Наука. -1981. –
- Джураев Х. Ш. Об одном регуляризирующих алгоритме получения приближений к нормальному решению вырожденных систем линейных алгебраических уравнений (СЛАУ) // Прикладная математика. Межвузовской сборник научных трудов. -М.: МГПИ им. В. И. Ленина,1986. -130 с.







