В статье описан опыт решения альтернативных прикладных задач с помощью формулы нахождения длины кривой. Приведен образец содержания разработанных авторами прикладных задач и выводы проведенного педагогического исследования. Разработанные задачи удовлетворяют требованиям к результатам по дисциплине «Математика» ФГОС СОО.
Ключевые слова: прикладные задачи, длина кривой, математические способности.
Порой кажется, что математика основного и школьного курса не даёт возможность учащимся видеть элементы той «высокой» математики, которая сокрыта от глаз внутри: программ, которые составляют программисты для работы многих приложений для широкого круга пользователей; расчетов при строительстве интересных сооружений и конструкций; тарифных планов мобильной связи; ипотечных и кредитных программ; условий получения кэшбека и т. д. Стоит отметить, что современная тенденция в сфере образования — приблизить математику к подрастающему поколению, облагородить математику прикладной составляющей, в качестве повышения значимости развития математических способностей, тоже не раскрывает научные аспекты «высокой» математики.
Увлекаясь составлением альтернативных задач, во избежание списывания, и, одновременно, повышая прикладную значимость задач, авторы убедили учащихся, что на самом деле много «высокой» математики содержится в расчетах профессионалов экономической сферы жизни общества. В старшей школе для современных учащихся со средней успеваемостью в курсе математического анализа педагоги аккуратно вводятся понятия производной и интеграла. Далее трепетно они открывают тайну связи этих понятий и откровенного взаимодействия между ними. В продолжении этих «педагогических рисков» приходится задуматься еще и о прикладной значимости материала.
Принимая во внимание тенденцию облагораживания довузовской математики прикладной значимостью, авторы в статье делятся опытом о применении на уроках математики старшего звена формулы длины кривой.
В рамках тематического планирования на уроках по вычислению интегралов учащимся были предложены задания, где нужно было вычислить длину кривой (в частности параболы) на заданном промежутке.
О формуле.
Если плоская кривая задана уравнением y= f (x), где f —гладкая функция на отрезке значений параметра [a,b], то длина кривой определяется по формуле:
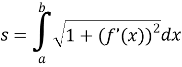
Задание.
Плоская кривая отнесена к прямоугольной системе координат и задана графиком функции на рисунке. Перечерти рисунок 1 в тетрадь и найди длину кривой на отрезке [-4; 4] (округли до десятых). Проверь полученный результат измерением кривой ниткой и измерь ее длину линейкой. Соотнеси полученный результат к единицам измерения длины. Начни выполнение задания с записи алгоритма необходимых действий.
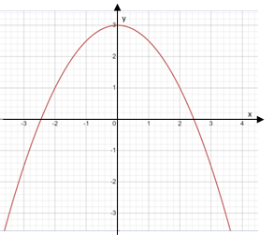
Рис. 1. График квадратичной функции
Решение:
Запишем алгоритм выполнения задания.
Алгоритм:
- Перечертить график заданной функции в тетрадь.
- Определить формулу кривой по ее графику.
- Найти производную функции, которая изображена на рисунке.
- Записать формулу для нахождения длины заданной кривой на заданном промежутке.
- Вычислить интеграл.
- Измерить ниткой длину кривой в тетради.
- Определить длину нитки по линейке.
- Сопоставить полученный результат с единицами измерения длины.
Необходимые вычисления.
По рисунку определяем формулу кривой: f(x)
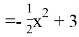
Найдем производную функции: f′(x)= — x
Запишем формулу нахождения длины кривой на заданном промежутке:
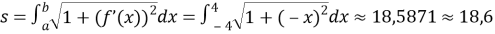
Выводы после измерения.
Кривая построена в тетради в обычном, общепринятом масштабе, — единичный отрезок 1 клетка. Длина нитки, которой измерили длину кривой на заданном отрезке, равна 9,3 см. Если взять за масштаб для построения графика функции единичный отрезок — 2 клетки, то есть 1 см, то мы получаем длину кривой в сантиметрах такую же, какая получилась при вычислении по формуле.
Педагогическое исследование на таких занятиях принесло много открытий для всех участников образовательного процесса. Используя метод наблюдения, и заполнение листов исследования оказалось, что процент вовлеченных учащихся был выше до конца одного урока, чем на занятиях по вычислению сложных интегралов. Выполнив подобные задания на протяжении двух уроков, созданный алгоритм вычисления по этой формуле, запомнился с легкостью.
Частью педагогического исследования являлось выявление сфер жизнедеятельности, где может использоваться эта формула.
Перечислим некоторые:
— в онлайн картах, определение длины пути при движении по кривой;
— при расчете воздушных и кабельных линий электропередач;
— при расчете расхода материала при изготовлении сварных конструкций, имеющих форму математических кривых;
Теоретическая часть исследования подтвердила высокую значимость подобных задач на уроках математики, так как общедоступных текстах ФГОС СОО читаем в требуемых результатах дисциплины «Математика». Изучение математики направлено на достижение целей: формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов; развитие логического мышления и алгоритмической культуры, пространственного воображения, математического мышления и интуиции, творческих способностей, необходимых для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности.
Стоит отметить, что для усиления результатов исследования материал использован в нескольких группах учащихся, без учёта уровня успеваемости. Для вычисления интеграла, из которого состоит формула, разрешалось пользование приложениями. Такой подход дал возможность вычисления большего числа кривых, которые использованы учащимися для сравнения результатов.
Приведем содержание еще одной прикладной задачи с использованием формулы длины кривой.
Задача.
На рисунке 2 изображена схема пролета воздушной линии, расположенной на местности без больших разностей уровней. Длиной пролета, или пролетом l, называют горизонтальное расстояние между точками крепления провода. Гибкая натянутая между двумя точками нить всегда провисает. Стрелой провеса f называют расстояние по вертикали между горизонталью, соединяющей точки крепления провода, и низшей точкой провода. Габаритом линии h называют наименьшее расстояние по вертикали от провода при его наибольшем провисании до поверхности земли, воды, крыш зданий, головки рельса и т. п.
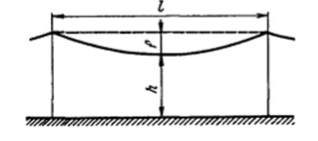
Рис. 2. Схема пролета воздушной линии
Вычисли длину провода в одном пролете воздушной линии, если длина пролета равна 100 м, а стрела провеса равна 3 метрам. Запиши алгоритм решения задачи.
Выполняя данное задание, учащиеся должны определить формулу параболы, которую описывает провод. Для этого необходимо поместить кривую на координатную плоскость, определить начало координат, вычислить значение коэффициентов квадратичной функции и, после использовать формулу для вычисления длины провода.
Подобные задания в практике работы составлены в большом количестве вариантов, с использованием возможностей приложения excel, для удобства расчетов (ответов) на все варианты. Варианты различаются числовыми значениями.
Применение прикладных задач при изучении сложных математических понятий и формул способствуют большему пониманию и усвоению, формируют математические знания, умения и навыки, а так же способствуют развитию математических способностей обучающихся. Такие альтернативные задания расширяют математические представления и дают возможность получить реальный опыт в самостоятельном применении математических знаний на практике, так как подобные задания не имеют готовых решений в сети интернет.
Литература:
- Федеральный государственный образовательный стандарт среднего общего образования (утв. приказом Министерства образования и науки РФ от 17 мая 2012 г. N 413) с изменениями и дополнениями от: 29 декабря 2014 г., 31 декабря 2015 г., 29 июня 2017 г., 24 сентября, 11 декабря 2020 г.
- Механический расчет линии электропередачи: Методические указания к семестровому заданию / Сост.; Волгоград. гос. техн. ун-т. — Волгоград, 2005. — 34 с.







