В статье автор описывает несколько расчетных моделей монолитных кессонных перекрытий с помощью программного комплекса ЛИРА-САПР и сравнивает их напряженно-деформированное состояние.
Ключевые слова : монолитное кессонное перекрытие, ЛИРА-САПР, компьютерное моделирование.
Снижение собственного веса монолитных перекрытий при сохранении ими требуемой прочности, надежности и долговечности является актуальной задачей строительства. Применение кессонных перекрытий позволяет существенно снизить нагрузки на вертикальные несущие конструкции, и как вследствие, значительно снижать расходы на весь несущий каркас здания.
Кессонное перекрытие представляет собой ребристую конструкцию, состоящую из плиты минимальной толщины, опирающейся по контуру на систему пересекающихся балок одинаковой высоты [1].
Все элементы системы жестко сопрягаются с друг другом и представляют собой единый диск покрытия.
Поиск эффективной расчетной модели кессонного перекрытия продолжается и по настоящий день. Причиной этого является неучёт таких факторов, как влияние продольных сил в отдельных элементах, переменность жесткостей ребер и стыковка в узлах.
Для построения правильной компьютерной модели необходимо обеспечить совместную работу плиты и балок. Для дальнейшего исследования мною представлены несколько способов расчета кессонных перекрытий с помощью программного комплекса ЛИРА. В качестве конкретного примера приведено монолитное кессонное перекрытие:
Прикрываемая площадь — 9х12 м
Расчетная длина балок перекрытия
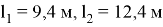
Толщина плиты — 60 мм
Сечение ребер — 200х480 мм
Шаг ребер — 1,5 м
Рассмотрим каждый вариант по отдельности.
Вариант № 1

Плита и ребра моделируются конечными элементами оболочек [3]. Преимуществом данных моделей является возможность моделирования плиты и ребер конечными элементами одинакового размера; однако такой способ моделирования затрудняет общую оценку напряженно-деформированного состояния перекрытия на участках с переменной жесткостью.
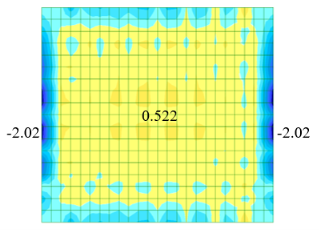
Рис. 1. Изополя изгибающих моментов Мх в плите
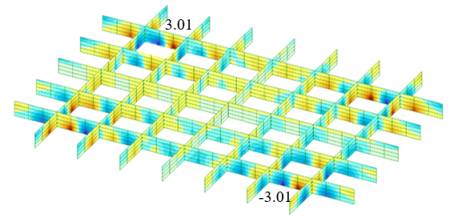
Рис. 2. Изополя изгибающих моментов Мх в ребрах
Вариант № 2
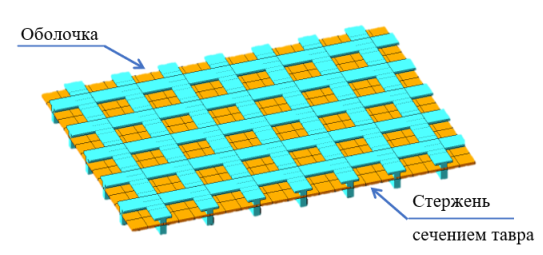
Плита моделируются оболочкой, а ребра — стержневыми КЭ таврового сечения [3]. В этой модели центр тяжести стержневого элемента совпадает со срединной поверхностью плиты. В данной методике неопределенным параметром является ширина свеса полки. В различных методических пособиях ширина свеса полки принимается разной (от 3 до 15 толщин плиты). В приведенном примере свесы полок были приняты
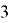

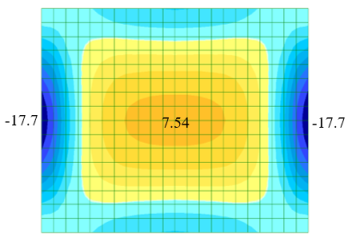
Рис. 3. Изополя изгибающих моментов Мх в плите

Рис. 4. Изополя изгибающих моментов Мх в ребрах
В этом случае значения изгибающих моментов в пролете плиты получаются большими по сравнению с моделью № 1.
Вариант № 3
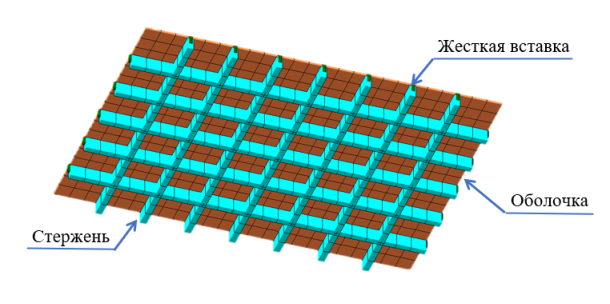
Плита моделируется двухмерными конечными элементами (КЭ) оболочек, а ребра плит — одномерными стержневыми элементами с введением абсолютно жестких вставок [2] для учета эксцентриситета балок на величину, равную
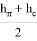
Наличие эксцентриситета балки приводит к возникновению в плите мембранной группы усилий, то есть сил, действующих в плоскости плиты (растяжение и сжатие).
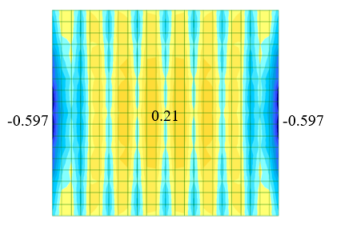
Рис. 5. Изополя изгибающих моментов Мх в плите
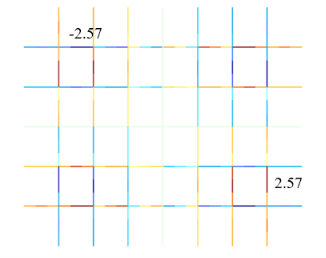
Рис. 6. Изополя изгибающих моментов Мх в ребрах
Проведенный анализ расчетов кессонного перекрытия по нескольким моделям показал работоспособность модели № 3 с жесткими вставками. Рассматриваемая модель показывает реальную работу кессонного перекрытия. На рис.5,6 видно, что плита передает усилия на стержни, воспринимая наименьший момент, что говорит о включении в работу плиты при изгибе балок.
Результаты расчета кессонного перекрытия с использованием ПК ЛИРА-САПР значительно (около 40 %) отличаются от расчета по аналитической методике [4], где плита рассчитывается отдельно как опертая по контуру, а ребра — как перекрестные балки.
В компьютерной модели перекрытия распределение усилий изменяется по сравнению с распределением усилий при аналитическом расчете в отдельных плитах, опертых на ребра. Поэтому усилия в балках при уменьшаются.
Конкретные расхождения с результатами компьютерного расчета заставляют допустить, что работа монолитного кессонного перекрытия в жизни отличается от компьютерной модели, которая не учитывает прежде всего характерное для железобетонных конструкций перераспределение усилий.
Литература:
- Лоскутов, И. С. Монолитные железобетонные кессонные перекрытия / И. С. Лоскутов. — Москва, 2015. — 72 c.
- Городецкий А. С., Евзеров И. Д. Компьютерные модели конструкций. — Москва: Издательство Ассоциации строительных вузов, 2009. — 360 с.
- А. С. Маркович. Практическая реализация математической (компьютерной) модели многоребристого перекрытия// Строительная механика инженерных конструкций и сооружения. 2016 (№ 2), стр. 39–44.
- Расчет и конструирование частей жилых и общественных зданий. Справочник проектировщика / под ред. П. Ф. Вахненко. Киев, 1987. с. 281–285.







