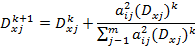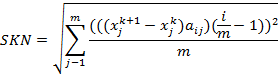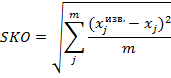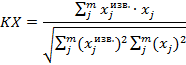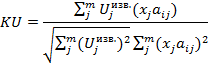В связи с ростом населения Земли, всё острее стоит вопрос нехватки ресурсов. Поэтому методология их поиска очень актуальна. Для осуществления геофизической разведки, особенную важность имеет решение обратных задач. Существует много разных подходов к данной проблеме. О некоторых из них речь пойдёт в этой статье.
Интегральная интерпретация данных – совместная обработка различных эмпирических данных, полученных несколькими методами, для построения общей картины.
Адаптивный метод – способ решения задач в которых число переменных больше чем число уравнений, путём постоянной подстройки под входные данные [1].
Геоинформационная система – система предназначенная для сбора, хранения, анализа и графической визуализации пространственных данных и связанной с ними информации о представленных в ГИС объектах.
Геофизическое исследование скважин – комплексное исследование скважин с целью сбора данных для последующей обработки в геоинформационных системах с использованием различных методов.
Прямая задача – исследование модели, в которой параметры считаются известными, для извлечения полезного знания об объекте.
Обратная задача – тип задач, часто возникающий во многих разделах науки когда значения параметров модели должны быть получены из наблюдаемых данных.
Для того, чтобы получить представления о свойствах объекта, необходимо создать его модель.
Модель будет включать в себя следующие параметры: глубины границ раздела слоев и свойства пород в каждом слое. Используя математические зависимости между элементами модели и полем, мы можем вычислить теоретические значения поля для заданных условий его наблюдения.
Процесс перехода от модели к полю называют решением прямой задачи. Переход от значения поля к параметрам модели среды – решением обратной задачи.
Одним из простейших вариантов решения обратной задачи является подбор такой модели, которая дала бы теоретическое поле, совпадающее или близкое к наблюдаемому [1].
В нашей статье предполагается, что имеется некоторая модель, характеризующаяся набором параметров. Это может быть вектор или набор векторов, матрица или набор матриц, и векторов.
Обозначим значения неизвестных параметров X {x1, x2, … xn}. Получим математическую модель, связывающую неизвестные значения параметров с некоторым наблюдением, представленные в виде системы линейных или нелинейных алгебраических уравнений U=AX или U=f(X).
Данная исследуемая модель имеет вид системы уравнений:
Сопоставляя прямую и обратную задачи, необходимо отметить следующие их особенности:
Прямая задача, как правило, имеет единственное решение. Заданной модели при заданных условиях наблюдения соответствует единственное поле. В обратной задаче - одному и тому же полю может соответствовать множество моделей. Поэтому при решении задач возникает вопрос: какой ответ мы получили единственный или один их множества и какой из множества ответов наиболее близок к реальному. Прямые задачи являются, как правило, устойчивыми. Обратные задачи очень часто оказываются неустойчивыми, т.е. небольшие искажения в данных наблюдений могут приводить к значительным погрешностям в параметрах модели.
Из общей статистической постановки вопроса нетрудно получить рекуррентный алгоритм, позволяющий уточнять оценки параметров, переходя последовательно от уравнения к уравнению. Достоинством рекуррентного метода является то, что он за один проход всех уравнений позволяет получить искомое решение и оценку ковариационной матрицы, а следовательно, и погрешности решений. Однако, он, как и многие другие методы, связанные с обращением и умножением матриц, позволяет решать системы с небольшим числом неизвестных [2]. Это обусловлено следующими причинами:
С ростом числа уравнений растут ошибки, связанные с умножением
матриц
Время счета растет пропорционально n3.
Память, необходимая для хранения ковариационных матриц, растет
пропорционально n2.
В связи с этим, возникла необходимость создания метода (в классе итерационных), который был бы лишен указанных недостатков [3].
В рамкой данной статьи будут рассмотрены 4 метода:
Адаптивный метод;
Метод Качмажа;
Метод Качмажа с регуляризацией;
Разностный метод.
Оцениваться результаты будут с помощью 4 показателей:
Среднеквадратичная невязка;
Среднеквадратичное отклонение;
Корреляция между исходными коэффициентами отражения и полученными;
Корреляция между исходной трассой и полученной.
Запишем формулы адаптивного метода. Метод Качмажа и Качмажа с регуляризацией являются его упрощением. Расчёт коэффициентов отражения в разностном методе происходит со сдвигом на 1 позицию [4].
Далее происходит расчёт разностей коэффициентов отражения.
После чего полученные результаты добавляются к результатам из адаптивного метода.
Каждое неизвестное на k+1 шаге будет равно:
где
![]() – номер шага уточнения (не является показателем степени),
– номер шага уточнения (не является показателем степени),
i – порядковый номер уравнения,
l – номер итерации,
n – число уравнений в системе,
j – порядковый номер неизвестного,
m – число неизвестных,
![]() – коэффициент в l-ом
уравнении j-го
неизвестного. В случае нелинейной системы он будет зависеть от k,
– коэффициент в l-ом
уравнении j-го
неизвестного. В случае нелинейной системы он будет зависеть от k,
![]() – оценка дисперсии
неизвестного на k-ом
шаге,
– оценка дисперсии
неизвестного на k-ом
шаге,
![]() – дисперсия ошибки
измерения параметра u
в i-ом
уравнении.
– дисперсия ошибки
измерения параметра u
в i-ом
уравнении.
Оценка дисперсии xj на каждом шаге уменьшается следующим образом:
На данный момент программа предусматривает оценку результатов по 4 критериям:
Среднеквадратичная невязка:
Среднеквадратичное отклонение коэффициентов:
Корреляция коэффициентов:
Корреляция трасс:
Разработок в данной области прикладной науки очень много, т. к. постоянно требуется улучшение точности получаемых результатов, однако, методов, которые показывают высокие характеристики точности и скорости достаточно мало [5].
Этот подход рассматривает два метода, которые впоследствии сравниваются между собой, в то время как наш использует четыре метода расчетов и сравнение между ними, что существенно повышает качество получаемых результатов. Оценка результатов осуществляется только по неквадратическому критерию оптимизации, в отличие от нашей работы, в которой реализованы четыре параметра, по которым осуществляется контроль получаемых данных.
Также хотелось бы отметить, что решения обратных задач, с которыми могут справиться данные методы, практически не ограничивают объем обрабатываемых данных [6].
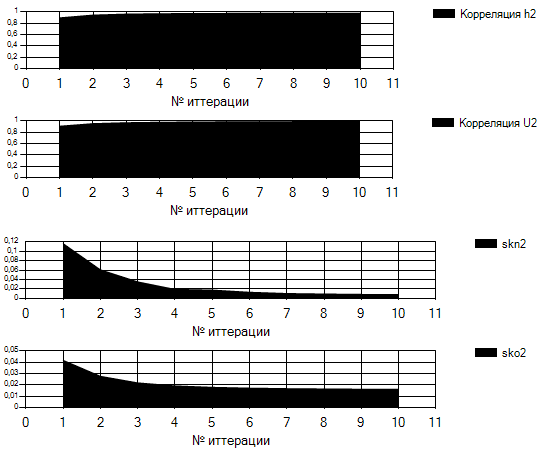
Было проведено несколько опытов. В них было определено, как влияют на скорость сходимости и точность методов, различные сигналы (коэффициент затухания, количество периодов и длина периода сигнала), количество взятых коэффициентов отражения, процент накладываемой помехи и её вид, а также, как влияет коэффициент регуляризации на три из четырёх методов и влияние начального Sigma на результаты адаптивного метода. Опыты проводились на модельных данных.
«Рис.» 1– Параметры оценки
Анализ особенностей методов позволяет сделать выводы, что адаптивный метод и методы производные от него, не накапливают ошибок округления и позволяет решать системы с большим числом неизвестных. В настоящее время реально решаются задачи с числом неизвестных 104 и более.
Может решать системы, где число неизвестных больше, чем число уравнений. Обладает гибкими свойствами регуляризации.
-
Литература:
Бизюкин, С.В., Кочнев В.А. Исследование возможностей адаптивного метода для решения обратной задачи МТЗ / В. А. Кочнев С. В Бизюкин // Геология и геофизика. – 1988. – № 7. С. 62-67.
Кочнев, В.А. Технология решения обратной динамической задачи по данным метода отраженных волн. / В. А. Кочнев И. В. Гоз В. С. Поляков // Труды международного семинара “Обратные задачи геофизики” Новосибирск. – 1996. – 30 сент.–4 окт. С. 80-92.
Кочнев, В.А. Путь осознания возможностей математических моделей и алгебраических уравнений в геофизике / В. А. Кочнев // Геофизика. – 2001. – № 5. С. 15-20.
Кочнев, В.А. Итерационный (адаптивный) подход к решению обратных геофизических задач. Математическое обеспечение и структура ЭВМ. [Текст]: сб.научн.работ / В. А. Кочнев. – Красноярск: ИПЦ КГТУ, 1997. – 623 с.
Заявка на пат. 98113007/25 Российская Федерация, МПК 6 G01V1/28, G01V1/00, G01V1/36. Способ определения глубинно-скоростных параметров среды и построения ее изображения по сейсмическим данным, система PRIME; заявитель Глоговский В.М. – 1 с.
Кочнев, В.А. Хвостенко, В.И. Адаптивный метод решения обратных задач гравиметрии. / В. А. Кочнев В. И. Хвостенко // Геология и геофизика. – 1996. – № 7. – С. 120-129.