Исследование распространения ультразвуковых волн в материалах позволяет определить постоянные упругости, знание которых способствует лучшему пониманию поведения конструкционных материалов. Постоянные упругости связаны с фундаментальными явлениями состояния твердого тела, такими как удельная теплоемкость, температура Дебая и параметры Грюнайзена. Постоянные упругости можно определить через скорости продольных и поперечных волн [1].
Скорости ультразвука и постоянные упругости связаны следующими соотношениями:
Модуль продольной
упругости:
![]() (1)
(1)
Модуль объемной упругости: K = L – (4/3)G (3)
Температура Дебая, которая используется для объяснения известной проблемы твердого состояния (колебания кристаллической решетки), тоже определяется через скорость. Соотношение выглядит так:
где:
-
 средняя
скорость звука;
средняя
скорость звука;
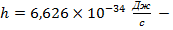 постоянная
Планка;
постоянная
Планка;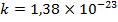
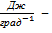 постоянная
Больцмана:
постоянная
Больцмана: число
Авогадро;
число
Авогадро;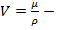 объем,
равный отношению молекулярной массы к плотности;
объем,
равный отношению молекулярной массы к плотности;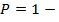 число
атомов в молекулярной форме.
число
атомов в молекулярной форме.
Постоянные упругости связаны с межатомными силами, координационными изменениями и т.д., а также с ударной нагрузкой, ростом разломов и трещин. В пористых материалах, например в литых металлах, керамике и большинстве композитов, соотношения между постоянными упругости и скоростью достаточно сложные. В этих материалах постоянные упругости являются функциями размера, формы и ориентации пор.
|
Al |
Cu |
Zn |
Ag |
Ni |
Ti |
|
6260 |
4700 |
4170 |
3600 |
5630 |
6230 |
|
|
3080 |
2260 |
2410 |
1590 |
2960 |
3180 |
|
|
26,09 |
63,55 |
65,37 |
107,86 |
58,7 |
47,95 |
|
|
2,70 |
8,93 |
7,13 |
10,5 |
8,8 |
4,54 |
|
|
L, ГПа |
70 |
100 |
99 |
136,08 |
279 |
176,15 |
|
L, ГП [5] |
105 |
197 |
123 |
143,1 |
311,5 |
112 |
|
G, ГПа |
25,6 |
45,6 |
41 |
26,6 |
77,44 |
45,9 |
|
G, ГПа [6] |
25,5 |
37 |
44,7 |
30,3 |
79,00 |
44 |
|
К, ГПа |
71,63 |
68,75 |
136,42 |
100,61 |
175,75 |
114,95 |
|
К, ГПа [7] |
43,05 |
111,28 |
77,8 |
100,7 |
175,71 |
115 |
|
λ, ГПа |
54,59 |
105,99 |
41,14 |
82,95 |
124,08 |
84,35 |
|
λ, ГПа [7] |
26,05 |
97,53 |
41,2 |
84,23 |
125,8 |
81,65 |
|
σ |
0,34 |
0,35 |
0,25 |
0,38 |
0,31 |
0,32 |
|
σ, [8] |
0,34 |
0,35 |
0,27 |
0,37 |
0,28 |
0,32 |
|
68 |
123 |
103 |
73,42 |
202,9 |
121,18 |
|
|
70 |
110 |
120 |
80 |
210 |
120 |
|
|
γ |
2,71 |
2,12 |
7,68 |
6,12 |
1,8 |
6,12 |
|
γ [10] |
2,11 |
2,06 |
2,00 |
2,5 |
1,73 |
1,23 [11] |
|
2538 |
2016 |
2092 |
1560 |
2440 |
2597 |
|
|
199 |
205 |
198 |
144 |
251 |
239 |
|
|
394 |
315 |
234 |
208 |
450 |
380 |
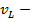 скорость
звука в продольной волне;
скорость
звука в продольной волне;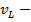 скорость звука в
поперечной волне;
скорость звука в
поперечной волне;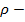 плотность вещества;
плотность вещества;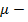 молекулярная
масса вещества.
молекулярная
масса вещества.
- Литература:
- Бергман Л. Ультразвук и его применение в науке и технике. М., Изд-во иностр. лит., 1956г.;
- Handbook of Chemistry and Physics. 33rd edition, Cleveland;
- Кэй Д., Лэби Т. Справочник физика-экспериментатора. Пер. с англ. М., Изд-во иностр. лит., 1949г.;
- Кэй Д., Лэби Т. Таблицы физических и химических постоянных. Пер. с англ. Под редакцией К.П. Яковлева. М., Физматгиз, 1962г.;
G. Mavko, T. Mukerji, J. Dvorkin. The Rock Physics Handbook. Cambridge University Press 2003;
- Беляев Н.М. Сопротивление металлов. - Москва: Наука, 1965г.;
- Ландау Л.Д., Лифшиц Е.М., Теория упругости, 4 изд., М., 1987;
- Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Ауксетическая механика кристаллических материалов. Известия РАН, МТТ, 2010, №4, стр. 43-62;
- Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: Лань, 1999г.-328с.;
- Urzendowski S.R., Guenther A.H. // Int. Symp. Therm. Expans Solids. 1974. P.256-277.
- Г.И. Канель, С.В. Разоренов, Е.Б. Зарецкий, Б. Херрман. Термическое “разупрочнение” и “упрочнение” титана и его сплава при высоких скоростях ударно-волнового деформирования. Физика твердого тела, 2003, том 45, вып. 4;
- Р.А. Лидин, В.А. Молочко, Л.Л. Андреева. Химические свойства неорганических веществ – «Химия», 2000г. – 286с.







