В статье представлены результаты исследования, разработки и оценки контекстной задачи для бинарных уроков, направленных на интеграцию дисциплин общеобразовательного и профессионального циклов. Коллективное решение производственных задач на основе конкретных ситуаций позволило объединять в единую систему оценивания математические знания и профессиональные компетенции, формируя общие компетенции будущих специалистов согласно ФГОС. Сотрудничество преподавателей разных циклов способствовало формированию и усилению мотивации студентов к процессу обучения.
Ключевые слова: контекстная задача, производственная задача, прикладная задача, оценка общих компетенций.
Результатом современного образования является умение ориентироваться в информационных потоках знаний, применять и преобразовывать их в умения. Это возможно средствами практико-ориентированных задач, к которым относятся контекстные задачи.
Контекстная задача — это задача мотивационного характера, в условии которой описана конкретная жизненная ситуация [1]. Контекстное обучение является средством решения профессиональных задач по специальности. Контекстные задачи близки к жизненным ситуациям, позволяют устанавливать связи между разными дисциплинами образовательного процесса и осуществлять поиск недостающей информации в сети интернет. Такие задачи формируют исследовательские навыки и развивают общие компетенции согласно ФГОС. Требованием к решению задачи является анализ, осмысление и объяснение конкретной ситуации или выбор способа действия в ней, а результатом решения задачи является встреча с учебной проблемой и осознание ее личностной значимости.
Любой производственный процесс сопровождается коллективным решением поставленной профессиональной задачи. Зачастую в образовательном процессе студент оценивается по принципу индивидуализации, контекстные же задачи позволяют выполнять задание в команде, тесно взаимодействовать с преподавателем, как с консультантом. Такая роль преподавателя дает возможность передать лекционную и теоретическую части материала в индивидуальном порядке. Разработка и оформление контекстных задач вынуждает преподавателей дисциплин разных циклов не только проявлять воображения, смекалку, умение сочинять увлекательный контекст, но и плотнее сотрудничать. В содержание мероприятий по сотрудничеству в обязательном порядке входит анализ тематического планирования разных дисциплин.
Совместная динамичная деятельность, межличностное взаимодействие, единство обучения и воспитания ставят контекстные задачи на лидирующие позиции среди форм организации учебной деятельности. Желательно контекстные задачи выполнять на бинарных уроках, являющихся формой реализации межпредметных связей и интеграции предметов. Такой нетрадиционный урок ведут два или несколько педагогов — предметников. Бинарный урок по своей природе является одной из форм проектной деятельности. Обычно это межпредметный внутренний краткосрочный или средней продолжительности проект. Решение прикладных и контекстных задач в области профессиональной деятельности на уроках математики и дисциплин профессионального цикла способствует формированию понимания того, что полученные знания и умения на уроках математики необходимы в профессиональной деятельности. Описание производственной ситуации в таких задачах способствуют вынужденному изучению текста, чтение становится осмысленным. Прикладная задача описывает профессиональную деятельность с использованием профессиональной терминологии, но с применением математического аппарата.
Несмотря на стремление создать максимально профессиональные отношения и достигнуть положительной мотивации к процессу профессионального обучения, невозможно отказаться от учебного этапа — оценки выполнения работы. Оценивание предметных результатов является недостаточным при выполнении такого объема работы. В связи с этим разработана система оценивания, дающая возможность оценить, наряду с предметными знаниями и умениями, признаки проявления общих компетенций, формирующих и развивающих мотивацию к образовательному процессу. Оценка значима на каждом этапе выполнения задания, каждая задача сопровождается системой оценивания как всего задания, так и его этапов.
Рассмотрим контекстную профессиональную производственную задачу, содержащую математический материал по стереометрии в соответствии с тематическим планированием дисциплины «Математика». Задача содержит темы по нахождению элементов стереометрических тел, объемов тел и площадей поверхностей, что очень актуально для решения профессиональных задач дисциплин профессионального цикла. Содержание задачи структурировано в таблице для облегчения визуального восприятия. Задания (учебные действия) сформулированы коротко и конкретно. Каждый выполненный этап задания подразумевает его оценивание. Содержание оценок отличается от оценивания обычной математической задачи традиционной формы обучения.
|
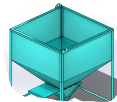
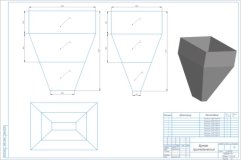
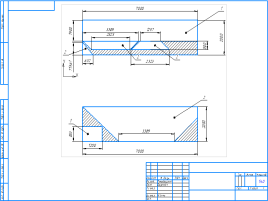
Задача Фирма «Буран» получила заказ на изготовление бункеров (крупноразмерных емкостей) от предприятия агропромышленной отрасли. Заказчик предоставил проект технического задания в виде чертежа 3d-модели и размеры заказа. |
|
|||
|
Исходные данные |
Основная часть (призма): 2000 х 2000 х 1500, мм Воронка (усеченная пирамида): высота боковой грани воронки — 1800 мм; нижнее основание — 2000х2000; верхнее основание — 400х400, мм. |
|||
|
Задания |
||||
|
Описание учебного действия |
Оценивание |
|||
|
Ознакомьтесь: |
|
|||
|
Повторите: |
|
|||
|
Разработайте: |
|
Оценка 1 Оценка 2 Оценка 3 |
||
|
Вычислите: |
|
Оценка 4 |
||
|
Моделируйте: |
|
Оценка 5 Оценка 6 |
||
|
Исследуйте: |
|
Оценка 7 Оценка 8 |
||
|
Рассчитайте: |
|
Оценка 9 Оценка 10 Оценка 11 |
||
|
Сравните: |
|
Оценка 12 Оценка 13 |
||
Математическая составляющая исследования
Математический (геометрический) аппарат, необходимого для нахождения объема и расхода материала частей бункера, как составного многогранника:
- площади четырехугольников;
- сечение многогранников;
- свойства равнобедренной трапеции;
- теорема Пифагора;
- длина ребер составного многогранника и т. д.
Математический аппарат для расчета при выполнении заказа в формулах
- Формула для нахождения площади трапеции
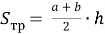
где
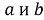
h – высота трапеции.
- Формула, которая необходима для вычисления объема усеченной пирамиды:
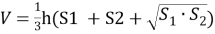
где h – высота усеченной пирамиды,
S 1 иS 2 – площади оснований
и т.д.
Математический аппарат для расчета при выполнении заказа в рисунка х
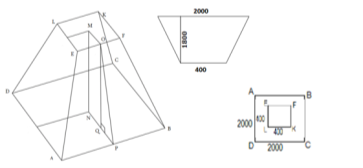
Рис. 1
Термины . Одним из этапов исследования являлось сравнение математических и профессиональных определений, которые описывают одно и то же понятие. Результаты исследования представлены в таблице 1.
Таблица 1
Об одном на разных языках
|
Производственная терминология |
Математическ ая терминология |
|
Расход материала на бункер |
Площадь полной поверхности |
|
Объём емкости (вместимость) |
Объем составного многогранника |
|
Воронкообразная емкость |
Усеченная пирамида |
|
Четырехугольная призматическая форма |
Параллелепипед |
|
Многоячейковая конструкция |
Составной многогранник |
|
Длина сварного шва |
Длина рёбер составного многогранника |
Уровни задачи [2]. Разработанная контекстная задача относится:
- к задачам уровня воспроизведения, так как близка к ситуации на производстве, проверяет умения выполнения математических действий с интерпретацией математических результатов;
- к задачам уровня установления связей, отражает математические и профессиональные взаимные связи;
- к задачам уровня рассуждений, так как не подсказывает метод решения, а заставляет исследовать задачу.
Оформление, отчетные материалы и оценивание. Решение задачи оформляется по требованиям, соответствующим содержанию задания. Для вычисления объёма бункера необходимо соблюдение: математических обозначений; последовательности вычисления; правил оформления. Следовательно, в системе оценивания предусмотрены оценки за решение математической и профессиональной частей контекстной задачи, что отражено в перечне оценок (таблица 2).
Таблица 2
|
Разделы оценивания |
№ оценки |
Примечание |
|
Математическая часть |
1,2,4,7,9, 10,11,13 |
Оценки 10,11,13 определяются коллегиально по результатам исследования контекстной задачи |
|
Профессиональная часть |
5,6,8,10, 11,13 |
Выполнив задание, студенты разрабатывали таблицу отчета (чек-лист) полученных результатов. Обучающийся должен проявить свои сформированные общие компетенции при разработке таблицы для отчета, чтобы не потерять важную информацию. Условия оценки заданий содержит оценку за содержание чек-листа. Оценивание выполненного отчета не относится к категории оценивания контроля знаний на уроках традиционной формы обучения. Стоит отметить, что студенты, вполне открыто оценивают свою работу ниже оценки «5» если при обсуждении содержания таблицы результатов обнаруживается потеря данных.
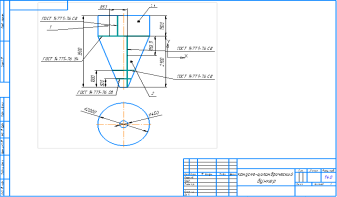
Исследование. Для выявления оптимального варианта был рассмотрен бункер цилиндрической формы. Студенты произвели расчеты для бункера цилиндрической формы, с сохранением габаритов бункера заказчика. Оказалось, что бункер был меньшего объема. Для сохранения объема был незначительно увеличен радиус. Заказчику будет предложено два оптимальных варианта.
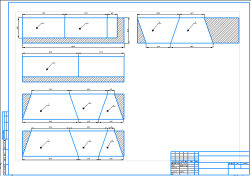
Чертежи и карты раскроя. После математических расчетов студенты выполнили чертеж и карту раскроя материала для призматического бункера, согласно заявке заказчика в программе «Компас».
Таблица 3
|
Чертеж призматического бункера |
Карта раскроя призматического бункера |
|
|
|
На основании расчетов оптимального варианта выполнен чертеж и карта раскроя цилиндрического бункера.
Таблица 4
|
Чертеж цилиндрического бункера |
Карта раскроя цилиндрического бункера |
|
|
|
Экономия . Себестоимость изготовления призматического бункера составила272840 руб. Для цилиндрического бункера понадобится меньше листов листового проката и с себестоимостью 170 525 рублей. Следовательно, цилиндрический бункер будет иметь меньший расход свариваемых материалов и меньшую длину сварочных швов, что в свою очередь уменьшит расход сварочной проволоки.
Вывод. Применение способов интеграции материала разных дисциплин при решении контекстных задач выявляет потребность в стойкой системе оценивания выполненных учебных действий, к тому же оценки нужны одновременно по двум дисциплинам. Задача имеет контекст, который затрагивает профессиональное содержание и требует оценивания профессиональных и общих компетенций. Значит, условия и критерии оценивания отличаются от традиционной.
Литература:
- Вербицкий А. Контекстное обучение в компетентностном подходе. Высшее образование в России. 2006 № 11
- Санина Е.И, Насикан И. В. Контекстные задачи по математике как средство развития функциональной грамотности обучающихся . Ученые записки Орловского государственного университета. № 1 (82), 2019 г.