В статье рассмотрены различные способы расчета монолитных безбалочных железобетонных перекрытий. Также проведено сравнение результатов расчета по современным отечественным и зарубежным методам расчета.
Ключевые слова: безбалочное перекрытие, метод предельного равновесия, метод конечно-элементного моделирования, метод заменяющих рам, метод прямого проектирования, Eurocode 2, ACI 318.
Безбалочное перекрытие состоит из плоской железобетонной плиты одинаковой толщины, опирающейся на ряд промежуточных колонн, на крайние колонны или на несущие стены.
Впервые конструкция здания с применением безбалочных перекрытий была использована в США в 1902 г. инженером Торнером [1]. В России такие перекрытия появились практически в то же время — в 1908 г. Под руководством инженера А. Ф. Лолейта было запроектировано и возведено четырехэтажное здания склада молочных продуктов. Особенностью данной конструкции было то, что колонны в них имели расширенный верх, что увеличивало площадь соприкосновения опор и плит, тем самым увеличивая надежность монтажа.
Впервые задумываться о проблемах расчета безбалочных перекрытий стали инженеры Дж. Р. Николсон (1914г.), Вестергард и Слейтер (1925г.) [2], а в СССР — Гвоздев А. А. и Мурашев В. И. (1933г.) [3]. Далее по результатам теоретических исследований и практических расчетов были сформированы первые нормативные документы для расчета безбалочных перекрытий [4] и [5], на основе которых были разработаны современные нормативные документы, регламентирующие расчет безбалочных перекрытий [6].
Отсутствие теоретических и экспериментальных исследований безбалочных перекрытий в ХХ. в. обусловило использование грубо приближенных методов расчета таких конструкций. В дальнейшем было предложено несколько различных по сложности и точности методов расчета безбалочных перекрытий.
Первые точные методы, в которых безбалочную плиту рассматривают как пластинку, опирающуюся на капители, предложили Лолейт и Штаерман. По способу Лолейта вся нагрузка (постоянная и временная) предполагается равномерно распределенной по всему перекрытию и передающейся по обоим направлениям. При квадратных панелях нагрузка, передающаяся в каждом направлении, равно половине общей нагрузки. Толщина плиты определяется по наибольшему по абсолютной величине (положительному) моменту в крайнем пролете, а моменты в остальных пролетах служат для подбора арматуры.
М. Я. Штаерман в [7] предложил упрощенный способ расчета безбалочных перекрытий, который базируется на схеме: плита и воображаемые балки, ширина которых равна половине пролета, а высота равна высоте плиты. Моменты рассчитываются отдельно для плиты и отдельно для балки.
Также существовали методы расчета с использованием бигармонических рядов (метод Галёркина) и метод расчета с использованием тригонометрических рядов (метод Леве), где безбалочное перекрытие рассматривается как плита, нагруженная сверху сплошной нагрузкой и снизу опорными реакциями капители, причем принимается, что это реактивное давление распределяется равномерно по всей площади капители. Данные методы были достаточно сложны и практически недоступны для проектировщиков, к тому же ряд положенных в основу этих методов предположений не соответствовал действительной работе плиты безбалочного перекрытия.
Далее появились упрощенные способы расчета, такие как метод упругих сеток и метод заменяющих рам. При расчете безбалочных перекрытий методом упругих сеток плита рассматривалась как система взаимно перпендикулярно пересекающихся нитей, которая в каждой точке пересечения должна находиться в равновесии. До приложения нагрузки сетка находится на условной координатной плоскости, а после приложения нагрузки точки пересечения нитей перемещаются относительно этой плоскости.
Расчет методом заменяющих рам предполагает рассматривать безбалочное перекрытие и колонны как две взаимно пересекающиеся рамы, ригель которой — плита шириной, равной полусумме смежных пролетов. Каждая из рам рассчитывается на полную приходящую на нее нагрузку. С учетом перераспределения моментов вследствие пластических деформаций, величины моментов в четырех расчетных сечениях панели плиты определяют с таким расчетом, чтобы сумма их равнялась балочному моменту.
Кандидат технических наук Шапошникова Юлия Александровна в своей диссертации [8] провела сравнительный анализ некоторых методов расчета безбалочных перекрытий. Перекрытие было рассчитано по следующим методам: Метод А. Ф. Лолейта, Метод М. Я. Штаермана, Метод бигармонических рядов, Метод заменяющих рам.
В данном исследовании рассчитывалась квадратная ячейка перекрытия пролетом 6м, толщина перекрытия была принята 200мм, нагрузка, приложенная на перекрытие принималась равной 15 кН/м 2 .
Главный вывод, который можно сделать по результатам анализа: значения моментов значительно отличаются друг от друга (в 2–5 раз), что говорит о несовершенстве методов статического расчета. Также данные способы расчета не учитывают влияния трещин и пластических свойств бетона, таких как усадка и ползучесть.
Современные отечественные нормы предписывают рассчитывать безбалочное перекрытие методом предельного равновесия. Согласно [9] и [10] данный метод предполагает двухстадийный характер деформирования материала. На первой стадии материал работает упруго и подчиняется закону Гука, то есть напряжение в нем не достигает предела текучести. На второй стадии в опасных сечениях при постоянной нагрузке начинают развиваться пластические деформации, нарушается линейная зависимость между напряжением и относительными деформациями. Суть метода состоит в том, что в стадии разрушения плита рассматривается как система звеньев, соединенных между собой линейными пластическими шарнирами.
Экспериментально установлено, что для безбалочного перекрытия наиболее опасными являются загружение полосовой нагрузкой через пролет и сплошной нагрузкой по всей площади перекрытия.
При загружении полосовой нагрузкой в предельном равновесии образуется 3 линейных пластических шарнира, соединяющих звенья в местах излома. Также образуется пластический шарнир в пролете по оси загруженных панелей.
При сплошном загружении плиты безбалочного перекрытия в средних панелях возникают линейные пластические шарниры, которые являются взаимно перпендикулярными и параллельными рядам колонн. При таком загружении каждая панель делится пластическими шарнирами на 4 звена, поворачивающихся вокруг линейных пластических шарниров, оси которых расположены в зоне капителей под углом 45° к рядам колонн.
Современные численные методы исследования конструкций приобрели большую популярность и являются мощным инструментом для решения сложных технических задач. Согласно [11] это метод решения уравнений равновесия, при котором исходная область определения функции разбивается на отдельные подобласти (конечные элементы). Расчет методом конечных элементов осуществляется с помощью различных программных комплексов САПР, например, ПК ЛИРА-САПР, SCAD Office, Robot Structural Analysis, Ansys и тд.
Моделирование зон опирания плиты перекрытия на колонны и стены выполняются при помощи функции АЖТ (абсолютно жесткое тело), что позволяет корректно учесть опорный контур плиты.
При расчете МКЭ существует линейная и нелинейная постановка задачи. При линейном расчете физическая нелинейность (неупругая работа конструкции) учитывается с помощью пониженных значений модуля упругости материалов в соответствии с п. 6.2.7 [12].
Также рассмотрим несколько зарубежных методов расчета, которые представлены в Европейских нормах (Еurocode2) и Американских нормах (ACI318).
В [13] содержится мало указаний по выполнению расчетов различных конструкций. Поэтому в [14] подробно рассмотрены 2 метода расчета плоских перекрытий: метод заменяющих рам и метод упрощающих коэффициентов.
Основная идея метода заменяющих рам в Еврокоде совпадает с идеей данного отечественного метода: конструкция разбивается на «рамы» по двум взаимно перпендикулярным направлениям. Эти «рамы» включают в себя полосы плит, которые рассматриваются как балки, и колонны. Отличием является ширина балки, принимаемая для расчета. Согласно [14] эта ширина зависит от направления приложения нагрузки, а также от соотношения сторон панели. Дальше расчет можно выполнять с помощью любого стандартного метода упругого метода, например, с учетом перераспределения моментов, согласно разделу 3.7.1 [14]. Полученные в ходе расчета изгибающие моменты следует распределять по полосам с учетом упругого поведения плиты.
Метод упрощающих коэффициентов применяется для жестких зданий с тремя приблизительно равными пролетами и плитами, которые в основном подвергаются действию равномерно распределенной нагрузки. В данном случае изгибающий момент и поперечные силы могут рассчитываться при помощи коэффициентов, указанных в разделе 3.8.1 [14]. Полученный данным образом изгибающий момент следует распределять по полосам в пропорции, указанной в табл. 3.7 [14].
В [15] представлены два метода расчета монолитных безбалочных перекрытий: метод прямого проектирования и метод заменяющих (эквивалентных) рам. Метод прямого проектирования состоит из набора правил по распределению моментов по секциям перекрытия, удовлетворяющим требованиям к безопасности и удобству эксплуатации конструкций. Для того, чтобы произвести расчет безбалочного перекрытия по данному методу, необходим осуществит три основных шага: определение полного статического момента, распределение суммарного статического момента на отрицательные и положительные и распределение отрицательных и положительных моментов по перпендикулярным друг к другу «секциям», включающим в себя колонны и полосы плит, которые в данном случае рассматриваются как балки. Распределение положительных и отрицательных моментов по «секциям» осуществляется согласно п. 8.10.5, 8.10.6 [15]. Следует отметить, что при определении коэффициентов для распределения моментов в пролетной полосе учитывается тип перекрытия — балочное/безбалочное, а в надколонной полосе — соотношение величины пролетов перекрытия, а в средней опорной полосе еще и параметр торсионной жесткости (параметр бэтта), который зависит от вида сопряжения колонны с плитой.
Согласно [15] основной идеей метода эквивалентных рам является представление трехмерной системы перекрытий через двумерные рамы, которые потом рассчитываются на нагрузки, действующие в плоскости рамы. Эквивалентные рамы состоят из трех частей: горизонтальные полосы перекрытия, колонны или другие вертикальные опоры, выступающие над и под плитой, и торсионные элементы, обеспечивающие передачу момента между горизонтальными и вертикальными элементами. После того, как были определены элементы заменяющей рамы, необходимо рассчитать жесткость каждого элемента (то есть, плитной части, колонны и торсионного элемента). Далее необходимо определить коэффициенты распределения моментов для неподвижных концов элементов рамы с помощью таблиц в прил. 20 [15]. После всех проделанных операций получается эквивалентная двумерная рама, состоящая из полосы перекрытия, колонны и торсионного элемента, которая должна быть рассчитана в расчетной программе.
В данной работе сравниваются результаты расчетов, полученных по следующим методам: Метод предельного равновесия (согласно СП63), Метод конечно-элементного моделирования (расчет производится в ПК ЛИРА-САПР), Метод заменяющих рам (Eurocode2), Метод прямого проектирования (ACI318).
На рисунке 1 представлена схема перекрытия для расчета.
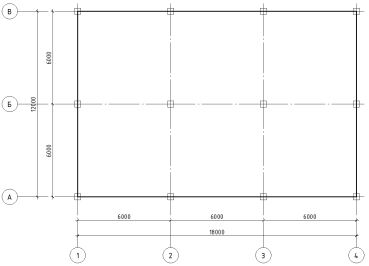
Рис. 1. Схема перекрытия
Толщина перекрытия принимается равной h = 200 мм, нагрузка, приложенная на перекрытие — сплошная равномерно распределенная нагрузка q = g + v = 1 т/м 2 .
Расчет производился для надколонной и пролетной полос. Результаты показаны только для надколонной полосы, так как они более наглядные
Таблица 1
Моменты, полученные для расчета по надколонной полосе
|
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
М7 |
|
|
СП |
3,16 |
3,16 |
3,16 |
3,16 |
3,16 |
3,16 |
3,16 |
|
МКЭ |
5,27 |
2,43 |
7,92/6,98 |
1,68 |
6,98/7,92 |
2,43 |
5,27 |
|
EU |
3,78 |
6,48 |
7,56 |
6,48 |
7,56 |
6,48 |
3,78 |
|
ACI |
1,22 |
2,45 |
3,29/3,06 |
1,65 |
3,06/3,29 |
2,45 |
1,22 |
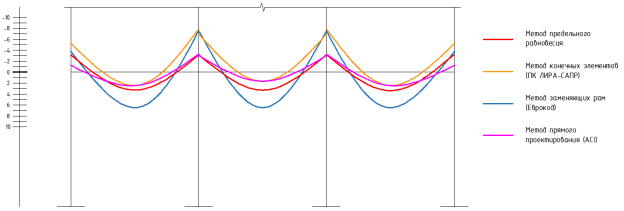
Рис. 2. Эпюра моментов для надколонной полосы
Исходя из полученных результатов можно сделать следующие выводы:
- Наибольшие пролетные моменты получаются при расчете методом заменяющих рам по EU2;
- Наибольшие опорные моменты получаются при расчете методом заменяющих рам по EU2 и методом конечных элементов;
- Наименьшие пролетные моменты получаются при расчете методом конечных элементов и методом прямого проектирования по ACI318;
- Наименьшие опорные моменты получаются при расчете методом прямого проектирования по ACI318;
- Моменты, полученные при расчете данными методами максимально различаются в 2,5 раза.
Литература:
- Владимиров Д., Кумпяк О. Г. Опорные зоны безбалочных перекрытий / Избранные доклады 64-й университетской научно-практических конференции студентов и молодых ученых, 2016 г.
- Генри Дж. Коуэн Строительная наука XIX-XX вв, М.: Энергоиздат, 1982 г. — 236 с.
- Мурашев В. И. Железобетонные конструкции: Общий курс: учеб. Для вузов по спец. «Промышленное и гражданское строительство» // Мурашев В. И., Сигалов Э. Е., Байков В. Н.; под ред. П. Л. Пастернака — М.: Госстройиздат, 1962. — 659 с.
- Руководство по расчету статически неопределимых железобетонных конструкций с безбалочными перекрытиями, — М.: Стройиздат, 1975–32 с.
- Руководство по проектированию железобетонных конструкций с безбалочными перекрытиями, — М.: Стройиздат, 1979–54 с.
- СП 63.13330.2018. Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52–01–2003. — Москва: Минрегион России, 2018 г.
- Штаерман М. Я. Безбалочные перекрытия / Штаерман М.Я, Ивянский А. М.// Государственное издательство литературы по строительству и архитектуре. — Москва, 1953г. — 335 с.
- Шапошникова Ю. А. Прочность монолитных безбалочных перекрытий с предварительно напряженной диагональной арматурой без сцепления с бетоном [Текст]: дис. … канд. тех. наук: 05.23.01: защищена 28.02.16 / Шапошникова Юлия Александровна. — М., 2016–204 с.
- Байков В. Н., Сигалов Э. Е. Железобетонные конструкции: Общий курс: [Для вузов по специальности «Пром. и гражд. стр-во»] / В. Н. Байков, Э. Е. Сигалов, 2-е изд., перераб. и доп. — Москва: Стройиздат, 1976;
- Бондаренко В. М., Суворкин Д. Г. Железобетонные и каменные конструкции: [Учеб. для вузов по спец. «Пром. и гражд. стр-во» и «С.-х. стр-во»]. — Москва: Высш. школа, 1987.
- Плоские безбалочные железобетонные перекрытия. Правила проектирования / НИИЖБ им. А. А. Гвоздева — Москва: ЦНИИПРОМИЗДАТ, 2017.
- СП 52–103–2007. Железобетонные и монолитные конструкции зданий
- EN 1992–1-1 Eurocode 2: «Design of concrete structures. Part 1: General rules and rules for buildings»
- Beeby A. W., Narayanan R. S. Designers’ guide to EN 1992–1-1 and EN 1992–1-2 / ICE Publishinh, 2011
- ACI 318–14 Building Code Req. for Structural Concrete — Commentary on Building Code Req. for Structural Concrete.







