Произведено моделирование цифрового фильтра с конечной импульсной характеристикой и частотной выборкой. Показано, что использование трёх элементарных цифровых фильтров расширило полосу пропускания.
Ключевые слова: цифровой фильтр, элементарный цифровой фильтр, конечная импульсная характеристика, моделирование.
Структурная схема цифрового фильтра (ЦФ) с конечной импульсной характеристикой (КИХ), реализуемого методом частотной выборки, приведена на рис. 1 [1].
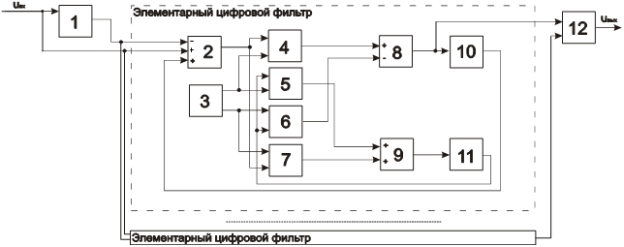
Рис. 1. Структурная схема цифрового фильтра
Реализуем её в среде Matlab-Simulink [2, 3]. Для этого, аналогично моделям, представленным выше, воспользуемся блоком подсистемы. Так как цифровой фильтр состоит из элементарных цифровых фильтров, внесём блок 1 структуры (рис. 1) в блок элементарного цифрового фильтра и реализуем элементарный цифровой фильтр независимо. Результат реализации элементарного цифрового фильтра представлен на рис. 2. При этом выбран высокий порядок — 4000. Модель для исследования работы представлена на рис. 3. Интервал дискретизации выбран равным 1/100000 с. Стоит заметить, что цифровой КИХ-фильтр прямой структуры реализации потребует уже 4000 операций умножения, в то время как в структуре их 4. Это лишний раз подтверждает высокую вычислительную эффективность представленного цифрового фильтра.
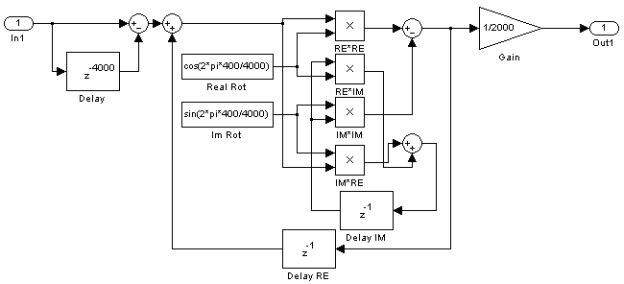
Рис. 2. Результат реализации элементарного цифрового фильтра
Результат работы модели представлен на рис. 4.

Рис. 3. Модель для исследования цифрового фильтра
Рассмотрим теперь синтез цифрового фильтра по методу частотной выборки на основе суперпозиции элементарных цифровых фильтров. Для этого организуем независимую подсистему, которая будет являться телом цифрового фильтра и содержать элементарные цифровые фильтры. На рис. 5 представлен цифровой фильтр, содержащий три элементарных цифровых фильтра.
Для сравнения характеристик на рис. 6 приведена модель, содержащая как цифровой фильтр (рис. 5), так и элементарный цифровой фильтр [1]. Результат работы модели приведён на рис. 7.
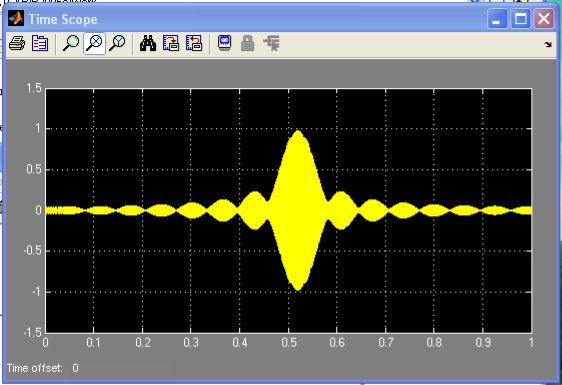
Рис. 4. Результат работы модели рис. 3.
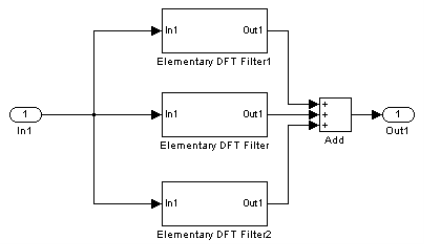
Рис. 5. Модель цифрового фильтра
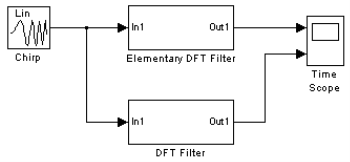
Рис. 6. Модель для исследования работы цифрового фильтра
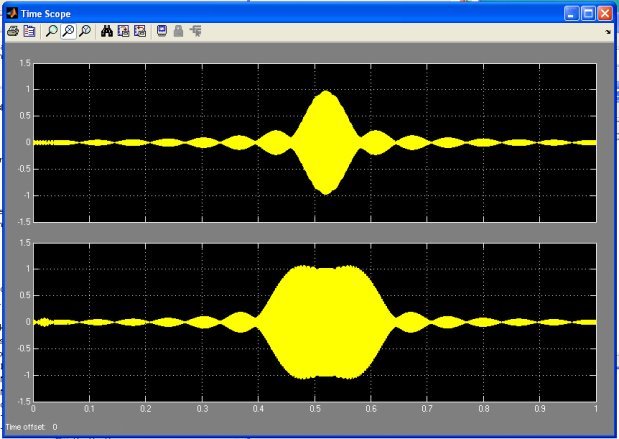
Рис. 7. Результат работы модели
По рис. 7 видно, что использование трёх элементарных цифровых фильтров расширило полосу пропускания. Таким образом, модель позволяет строить вычислительно-эффективные цифровые фильтры по методу частотной выборки.
Литература:
1. Иванов, В. В. Генераторные, фазовые и частотные преобразователи и модуляторы [Текст] / В. В. Иванов, В. К. Шакурский — М.: Радио и связь, 2003. — 172 с.
2. Андреев, И. В. MATLAB для DSP: SPTool — инструмент для расчёта цифровых фильтров и спектрального анализа сигналов [Текст] / И. В. Андреев, А. А. Ланнэ // Цифровая обработка сигналов. 2000, № 2. — С. 6–13.
- Гадзиковский, В. И. Теоретические основы цифровой обработки сигналов [Текст] / В. И. Гадзиковский. — М.: Радио и связь, 2004. — 378 с.







