Описаны основные характеристики цифровых фильтров, включая фильтры с конечной импульсной характеристикой. Показано, что изменение частоты дискретизации позволяет практически плавно изменять крутизну фазочастотной характеристики фильтра.
Ключевые слова: цифровой фильтр, конечная импульсная характеристика, фазочастотная характеристика.
Проблемой, ограничивающей использование цифровых фильтров (ЦФ) в различных системах передачи данных, является необходимость работы в широком диапазоне частот. При увеличении частот использования ЦФ уменьшается интервал дискретизации, что ограничивает максимально допустимый порядок цифровых фильтров.
Главной характеристикой ЦФ является алгоритм фильтрации. По алгоритму фильтрации осуществляется реализация фильтра.
Импульсной характеристикой ЦФ h ( n ) является реакция фильтра на единичный импульс при нулевых начальных условиях. Импульсная характеристика позволяет определить выходной сигнал фильтра по формуле дискретной свёртки входного сигнала [1].
С импульсной характеристикой фильтра связана передаточная функция H ( z ). Она определяется как отношение Z -преобразований выходного и входного сигналов. Импульсная и передаточная функции связаны парой Z -преобразований. С помощью передаточной функции H ( z ) так же можно найти реакцию фильтра на любое входное воздействие.
Комплексная частотная характеристика фильтра H exp( jT ) определяется как отношение преобразований Фурье выходного и входного сигналов при нулевых начальных условиях. Комплексная частотная характеристика равна значениям передаточной функции на единичной окружности Z -плоскости, и связана с импульсной характеристикой парой преобразований Фурье. Комплексная частотная характеристика является периодической по частоте с периодом, который равен частоте дискретизации [2].
Импульсная характеристика, передаточная функция и комплексная частотная характеристика дают полное описание ЦФ как линейной стационарной системы.
Модуль комплексной частотной характеристики рассматривают как амплитудно-частотную характеристику A ( T ) (АЧХ), а аргумент — как фазочастотную характеристику ( T ) (ФЧХ). Они также являются периодическими функциями с периодом, который равен частоте дискретизации.
По алгоритму работы ЦФ делятся на рекурсивные и нерекурсивные.
В рекурсивных алгоритмах фильтрации процесс вычисления выходного сигнала в заданный момент времени осуществляется с использованием предыдущих отсчётов входного и выходного сигналов. В рекурсивных фильтрах имеет место обратная связь. Количество используемых отсчётов выходного сигнала характеризует глубину рекурсии [3].
В нерекурсивных алгоритмах фильтрации процесс вычисления выходного сигнала в заданный момент времени осуществляется только с использованием предыдущих отсчётов входного сигналов. Обратная связь отсутствует. Нерекурсивные алгоритмы являются частными случаями рекурсивных алгоритмов при глубине рекурсии равной нулю.
В зависимости от расположения нулей передаточной функции на Z -плоскости различают фильтры минимально-фазового и неминимально-фазового типа. У минимально-фазовых фильтров A ( T ) и ( T ) связаны между собой парой дискретных преобразований Гильберта.
У неминимально-фазовых фильтров A ( T ) и ( T ) являются независимыми. То есть, при неизменной A ( T ) можно получить необходимую характеристику ( T ). Кроме этого, в классе неминимально-фазовых фильтров существуют фильтры с идеальными линейными ( T ).
Последнее свойство ЦФ является наиболее важным, так как позволяет выполнить условие линейности характеристик разработанных генераторных преобразователей, обладающих повышенной чувствительностью.
Рассмотрим условия реализации ЦФ с линейными ФЧХ [4]. Их реализация возможна в классе одномерных скалярных вещественных стационарных нерекурсивных линейных неминимально-фазовых цифровых фильтров.
Известны 4 вида фильтров с линейными ФЧХ.
Фильтры вида 1 имеют импульсную характеристику симметричную относительно центра, а значение отсчётов импульсной характеристики
М
является чётным:
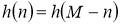
В фильтрах 2-го вида импульсная характеристика симметрична относительно центра, а значение отсчётов импульсной характеристики
М
является нечётным:
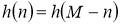
У фильтров вида 3 импульсная характеристика асимметрична относительно центра, а значение отсчётов импульсной характеристики М является чётным:
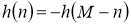
У фильтров вида 4 импульсная характеристика антисимметрична относительно центра, а значение отсчётов импульсной характеристики
М
является нечётным:
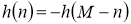
Сравнительный анализ фильтров указанных видов показывает, что предпочтение следует отдать фильтрам вида 1. Используя метод «окон» получим фильтры с конечной импульсной характеристикой или КИХ-фильтры.
ЦФ с конечной импульсной характеристикой (КИХ) имеют один неоспоримый плюс: линейные фазочастотные характеристики.
ФЧХ КИХ-фильтров ступенчатые и всегда проходят через начало координат, либо смещены на 90 градусов. Для получения большей точности необходимо увеличивать частоту дискретизации системы. Однако быстродействие процессора не всегда позволяет получить необходимую частоту дискретизации, а, соответственно, и точность.
Кратко остановимся на двух характеристиках КИХ-фильтров.
Как уже отмечалось выше, ФЧХ КИХ-фильтров является ступенчатой прямой, проходящей через начало координат или с постоянным смещением относительно начала координат. Чтобы фазовый сдвиг изменился скачком на одну ступеньку, надо чтобы период входного сигнала фильтра получил приращение, равное периоду дискретизации. Крутизна ФЧХ S зависит от порядка фильтра R и частоты дискретизации F d :
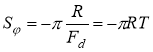
Порядок фильтра определяется количеством отсчётов КИХ, длина которой равна RT . Порядок фильтра в основном определяет форму АЧХ. Изменение порядка фильтра приводит к скачкообразному изменению крутизны ФЧХ, поэтому этот способ настройки ФЧХ не подходит.
Изменение частоты дискретизации позволяет практически плавно изменять крутизну ФЧХ. Этот способ настройки ФЧХ наиболее удобен.
Литература:
1. Антонью, А. Цифровые фильтры: анализ и проектирование [Текст] / А. Антонью; Пер. с англ. — М.: Радио и связь, 1983. — 320 с.
- Гадзиковский, В. И. Теоретические основы цифровой обработки сигналов [Текст] / В. И. Гадзиковский. — М.: Радио и связь, 2004. — 378 с.
- Голденберг, Л. М. Цифровая обработка сигналов: Справочник [Текст] / Л. М. Голденберг, Б. Д. Матюшкин, М. Н. Поляк и др. — М.: Радио и связь, 1985–312 с.
- Сергиенко, А. Б. Цифровая обработка сигналов [Текст] / А. Б. Сергиенко. — СПб.: Питер, 2004. — 608 с.







