Произведено моделирование прямой структуры цифрового фильтра с конечной импульсной характеристикой. Показано, что расхождение между расчётной АЧХ и огибающей выходного сигнала модели объясняется наличием шумов квантования и динамической работой системы.
Ключевые слова: цифровой фильтр, среда Matlab, моделирование.
Рассмотрим реализацию прямой структуры КИХ-фильтра в среде Matlab-Simulink. Как следует из [1] для реализации прямой структуры потребуются блоки задержки сигнала, умножители и блок суммирования. Далее строим модель цифрового фильтра (ЦФ); результат приведён на рис. 1.
В качестве коэффициентов выбраны значения 1/8 = 0,125, что соответствует импульсной характеристике фильтра скользящего среднего, имеющей прямоугольную форму [2].
Соберём следующую модель для исследования работы ЦФ (рис. 2).
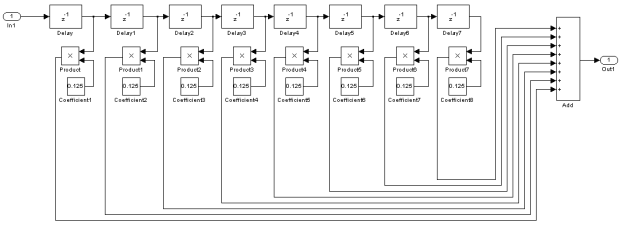
Рис. 1. Модель цифрового фильтра

Рис. 2. Модель для исследования цифрового фильтра
Для проведения исследования работы ЦФ, в данном случае это интегратор, являющийся фильтром низких частот (ФНЧ), подключим на вход синусоидальный источник с линейно изменяющейся частотой. Огибающая выходного сигнала будет соответствовать амплитудно-частотной характеристикой исследуемого фильтра.
Результат работы модели рис. 1 виден на осциллографе (рис. 3).
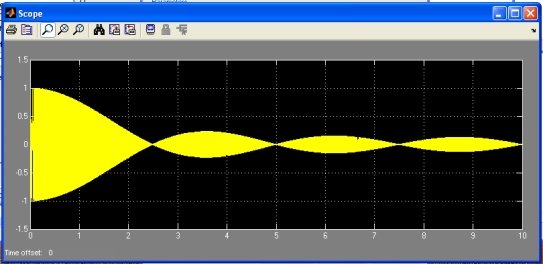
Рис. 3. Результат работы модели рис. 1.
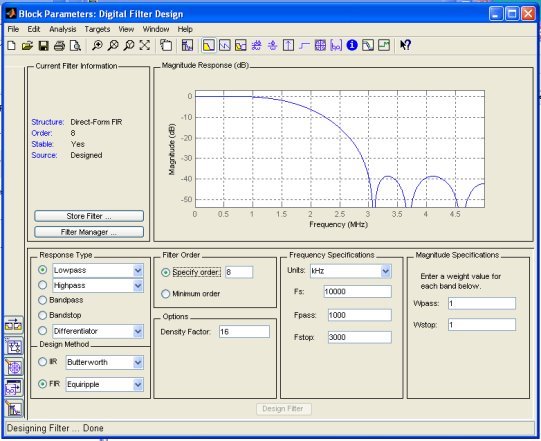
Рис. 4. Синтез цифрового фильтра
Для построения модели требуется знать значения коэффициентов импульсной характеристики цифрового фильтра (рис. 4). Для этого перейдём на вкладку импульсной характеристики и включим численную информацию по отсчётам импульсной характеристики (рис. 5).
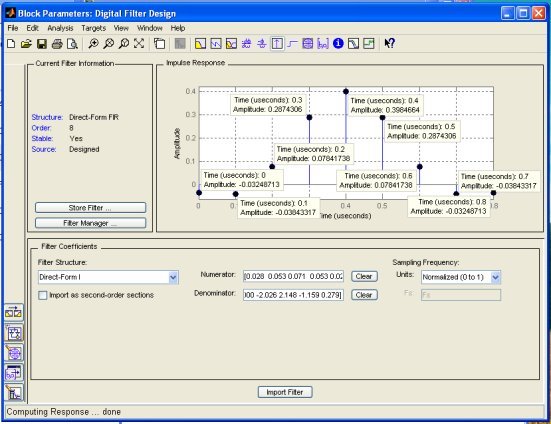
Рис. 5. Значения коэффициентов импульсной характеристики
В соответствии с синтезированными значениями импульсной характеристики заполним значения констант в модели, представленной на рис. 1. Результат заполнения представлен на рис. 6.
Так как полоса подавления начинается на частоте 3 кГц, настройки источника сигнала оставим прежними [3]. Результат работы модели рис. 6 представлен на рис. 7. Расхождение между расчётной АЧХ, представленной на рис. 4 и огибающей выходного сигнала, представленной на рис. 7, объясняется наличием шумов квантования и динамической работой системы.
Из результатов моделирования следует, что созданная в ходе диссертационного исследования структурная модель цифрового фильтра адекватна, и может быть использована при моделировании и исследовании цифровых фильтров в среде Matlab-Simulink.
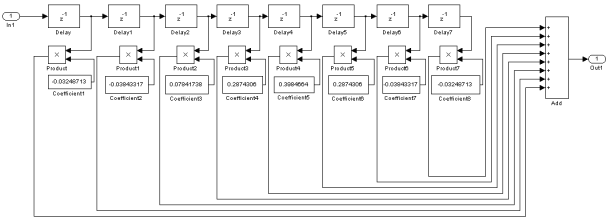
Рис. 6. Модель цифрового ФНЧ
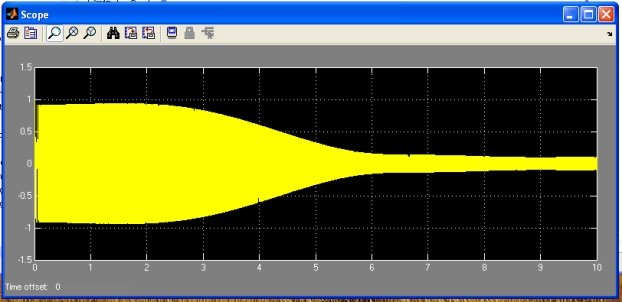
Рис. 7. Результат работы модели рис. 6.
Литература:
1. Сергиенко, А. Б. Цифровая обработка сигналов [Текст] / А. Б. Сергиенко. — СПб.: Питер, 2004. — 608 с.
- Гадзиковский, В. И. Теоретические основы цифровой обработки сигналов [Текст] / В. И. Гадзиковский. — М.: Радио и связь, 2004. — 378 с.
3. Иванов, В. В. Генераторные, фазовые и частотные преобразователи и модуляторы [Текст] / В. В. Иванов, В. К. Шакурский — М.: Радио и связь, 2003. — 172 с.







