В статье рассмотрены применения эволюционных алгоритмов оптимизации при размещении компенсирующих устройств в электроэнергетических системах, а также приведен сравнительный анализ классических методов и эволюционных алгоритмов.
Ключевые слова: генетический алгоритм, решение, локальный экстремум , оптимальное решение, алгоритм, компенсация реактивной мощности
Максимальная экономия энергетических ресурсов на сегодняшний день является одной из наиболее актуальной задачи в энергетике. Эта задача сводится к снижению потерь электроэнергии. В настоящее время качество электроэнергии в сети становится серьезной проблемой, которую необходимо изучить, чтобы добиться надежной системы электроснабжения. Компенсация реактивной мощности системы является одним из решений. Такая компенсация влияет не только на устойчивость системы, но и на ее надежность, что в настоящее время является приоритетом для получения качественной и надежной электроэнергии.
Проблемы с реактивной мощностью всегда связаны с уровнем напряжения, коэффициентом мощности, потерями и стабильностью мощности системы.
Различные задачи математического моделирования и математической статистики сводятся к экстремальным задачам, то есть к нахождению экстремума некоторой функции. Из-за некоторых определенных особенностей такие задачи формируют определенный класс целевых функций. Эволюционные алгоритмы можно отнести к «nature inspired» процессам, иными словами, «позаимствованным у природы». Эти алгоритмы используются при комбинаторной оптимизации. [2]
Эволюционные алгоритмы — это методы стохастического поиска, которые имитируют естественную биологическую эволюцию и (или) социальное поведение, разновидности. Такие алгоритмы были разработаны, чтобы прийти к почти оптимальным решениям в крупномасштабных задачах оптимизации, для которых классические математические методы не подходят из-за больших погрешностей.
Использование алгоритмов оптимизации позволяют определить вариант компенсации, при которых потери в СЭС будут минимальны или позволяют определить варианты расположения устройств компенсации реактивной мощности в сети.
Большое количество алгоритмов оптимизации обязательно поднимает вопрос о лучшем алгоритме оптимизации. Конечно, если существует оптимальный алгоритм оптимизации, то все остальные алгоритмы были бы излишними. Но универсального алгоритма оптимизации, который может решить все проблемы в энергосистеме, возникающие на практике, не существует. Все известные алгоритмы оптимизации в настоящее время могут быть использованы без ограничений только в конкретных областях. По характеру конкретной проблемы два различных алгоритма могут предложить несколько решений. Рассмотрим один из наиболее популярных алгоритмов оптимизации компенсирующих устройств в электроэнергетике: генетический алгоритм.
Первый эволюционный алгоритм в литературе был представлен в виде генетического алгоритма (ГА). [1] ГА был разработан на основе дарвиновских принципов «выживания наиболее приспособленных» и естественного процесса эволюции через воспроизводство. ГА продемонстрировал способность почти всегда находить оптимальные решения во многих проблемах техники. Несмотря на свое преимущество, ГА может потребовать длительное время для обработки результатов при поиске оптимального решения для развития. В попытке сократить время обработки результатов и улучшить качество решений, были предложены улучшения ГА, а также разработаны новые ЭА: от алгоритма имитации роста растений и алгоритма прямого поиска до алгоритма поиска кукушки и алгоритма цветочного опыления.
При сравнении классических методов и ЭА важно сказать, что наиболее фундаментальное различие между этими алгоритмами оптимизации состоит в том, что классическая оптимизация может найти только локальный экстремум, а ЭА пытается найти глобальный экстремум. ЭА не всегда находят глобальный экстремум, но находят достаточно хорошие решения, которые близки к глобальному.
Классические алгоритмы не имеют возможности избежать первого локального экстремума, который они находят, потому что они не допускают ухудшения качеств. ЭА, в отличие от классической оптимизации, имеют возможность уйти от этого локального экстремума и продолжить поиск наилучшего варианта.
ГА является интеллектуальной формой метода проб и ошибок, и основан на улучшении приспособленности биологических систем.
ГА работает со случайной совокупностью решений (хромосомы), которые состоят из множества элементов — ген . Пригодность каждой хромосомы определяется путем сравнения его с целевой функцией — приспособленность живого организма. При имитации естественного выживания наиболее приспособленного процесса, лучше всего хромосомы обмениваются информацией (через кроссовер или мутацию) для получения хромосом потомства. [3]
При применении данного алгоритма к задаче распределения избыточной реактивной мощности
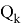
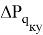

В основном, данный алгоритм реализуется на базе Mathcad, где целевая, как было уже сказано ранее, является приспособленностью живого организма, а оптимальное решения эквивалентно понятию фенотип. Мощность компенсирующего устройства в i-м узле преобразуется в хромосому при помощи функции кодирования. Функция декодирования восстанавливает решение обратным преобразованием. [2]
Решение поставленной задачи сводится к нахождению экстремума некоторой функции приспособленности из допустимых значений мощностей компенсирующих устройств — популяций.
Для наглядности приведу обобщенную блок-схему генетического алгоритма при поиске оптимального размещения компенсирующих устройств в сети (рис. 1).
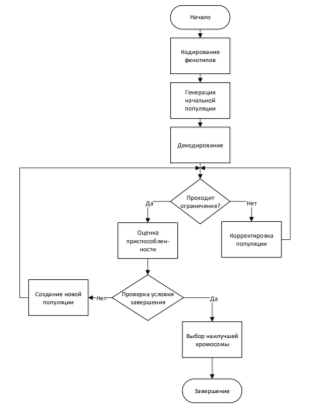
Рис. 1. Блок-схема генетического алгоритма
ГА, используемый в энергетике, представляет собой устойчивое состояние (потомок заменяет худшую хромосому, только если она лучше) и кодируется вещественно (переменные представлены действительными числами).
Соответственно, для значений, которые находятся в пределах 9–10 % от всех возможных решений, мы можем получить решения, которые удовлетворяют требованиям поиска. Данный алгоритм значительно сокращает время вычислений и дает значительно точные показатели. [4]
Для достижения энергоэффективности и повышения надежности в промышленных сетях необходимы различные подходы при оптимизации сети. Эволюционные методы позволяют улучшить технико-экономические показатели сетей и улучшить показатели сети в целом.
В наше время технологии достаточно активно интегрируются во все сферы жизни, и энергетика не является исключением. Для достижения энергоэффективности в промышленных сетях, проектируемых инженерами, были разработаны различные методы математического программирования, главный критерий которых — оптимальность. Это показатель, оценивающий эффективность затрачиваемых ресурсов, отрабатываемых при использовании данного решения.
Математические постановки реальных задач выводятся при определенных предположениях и даже с этими предположения, решение в крупномасштабных энергосистемах непросто. Есть много неопределенности в проблемах энергосистемы, потому что мощности системы большие, сложные и географически широко распределены. Поэтому получить решение на глобальном уровне достаточно сложно и решение математической оптимизации ищется обычно на местном уровне. Эти факты затрудняют эффективное решение многих проблем энергосистемы только через строгие математические формулировки.
В данной статье был рассмотрен один из наиболее известных методов оптимизации размещения компенсирующих устройств — генетический алгоритм. Можно выделить следующие достоинства этого метода: возможность параллельной работы с несколькими альтернативными решениями; высокая скорость сходимости к точке экстремума; работа не только с непрерывные, но и дискретными переменными, а также с многоцелевыми задачами. [5]
Литература:
- Holland J. Adaptation in natural and artificial systems. Ann Arbor, MI: University of Michigan Press; 1975.
- Vasiljevic D. Classical and Evolutionary Algorithms in the Optimization of Optical Systems. Springer, Boston, MA; Kluwer Academic Publishers 2002.Pages 279.
- Влацкая Л. А., Семенова Н. Г., Применение генетических алгоритмов в задачах оптимизации размещения компенсирующих устройств // Электротехнические системы и комплексы. 2019. № 4(45). С. 21–28
- Кремер О. Б., Подвальный С. Л. Программная реализация решения оптимизационных задач методом генетического алгоритма // Вестник ВГТУ. 2017. С.23–24
- Нелюбов В. М., Пилипенко О. И. Электрические сети и системы: учеб. пособие. / Оренбургский гос. ун-т. Оренбург: ОГУ, 2018. 188с







