В данной статье рассмотрены комплексные показатели оптимальных конструкций радиоэлектронной аппаратуры, отображающие основные функциональные и конструктивные характеристики её устройств в виде системы критериальных уравнений, полученных методами теории подобия. Все показатели физических процессов и функциональные характеристики аппарата представлены как гиперслучайные функции.
Ключевые слова: радиоэлектронные средства, оптимальные конструкции, гиперслучайные функции.
Введение. Во время проектирования радиоэлектронного средства (РЭС) пытаются получить оптимальное техническое решение в виде комплекса функциональных и конструктивных показателей, которые лучше всего соответствуют тем, что были заданы в техническом задании (ТЗ). На первых этапах проектирования необходимо создать математическую или физическую модель РЭС на основе известных физических законов и математических методов, отражающих процессы в нем, учитывая вероятность физических процессов и функциональных характеристик. Все эти характеристики должны быть отражены в целевой функции (ЦФ) — комплексном показателе, который объединяет все определяющие параметры и полностью характеризует свойства РЭС. Наилучшие (оптимальные) РЭС могут быть созданы методами, основой которых является гиперслучайные (ГВ) математические модели, комплексная ЦФ, которая отражает функциональные и конструктивные показатели устройства, и дает возможность их проектирования и оптимизации с помощью системы автоматизированного проектирования (САПР).
Гиперслучайные математические модели энергетических процессов в РЭС
Наиболее адекватные математические модели энергетических процессов, осуществляемых в РЭС, отражаются как скалярные и векторные функции, когда каждая из физических величин рассматривается как ГВ, с соответствующими вероятностными характеристиками [1].
Для отображения ГВ величин и функций использованы обозначения: hV(x) — ГВ величины х, hFs(Х) — ГВ скалярной функции множества Х, hFv(Y) — ГВ векторной функции множества Y ; символ «→» — общее обозначение ГВ величины или функции.
Функционирования РЭС — это передача и преобразование энергетических потоков электромагнитного поля, теплового, механического, информационного; гиперслучайные математические модели для этих основных процессов можно получить из системы уравнений Лагранжа второго рода [2], если каждое из них подать в гиперслучайной форме:
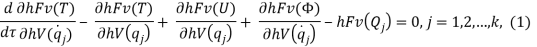
где T — кинетическая энергия, U — потенциальная; Φ — функция рассеяния энергии; Q — обобщенная сила;
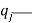
Выражения для различных форм энергии и функции рассеивания энергии как функций обобщенных координат q:
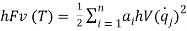
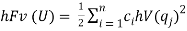
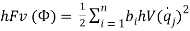
Вероятностные характеристики исходных параметров РЭС могут быть получены на основе теории ГВ явлений быстрее и с меньшим количеством вычислений, которые нужно производить по имитационному моделированию с применением, например, метода Монте-Карло.
Создание ЦФ РЭС методами теории сходства
Теория подобия [3] дает возможность сформировать выражение для ЦФ РЭС в виде системы критериальных уравнений, в которую входят безразмерные критерии
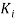
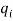
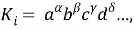
где a, b, c, d ... – размерные параметры, α, β, γ, δ, ... — коэффициенты влияния соответствующего размерного параметра на критерий
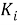
Единичные критерии
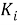
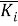
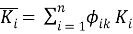
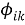
Система n частных критериев
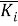
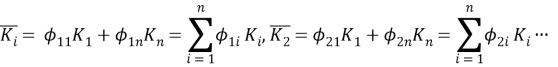
(2)
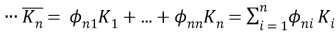
Функции
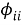
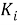
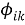
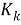
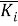
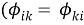
Формирование частного и комплексного критерия
Частный критерий макропоказателей конструкции
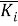

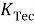
Критерий


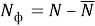
Соотношение
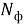
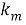
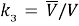
Поскольку критерии качества должны быть безразмерными, критерий использования объема РЭС создан в виде:
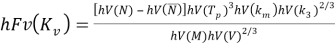
где
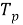
Показатели степени для
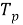
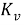
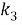
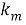
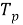
ГВ свойства у выражения
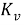
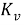
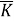
Технологическое совершенство конструкции может быть определено с помощью основных показателей технологичности: критериев уровня технологичности
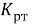
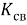
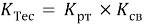
Частный критерий макропоказателей всей конструкции:
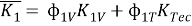
Приоритеты
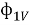
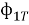
Частный критерий
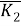
Совершенство системы защиты РЭС от вибрационных и ударных воздействий оценены критериями динамического усиления
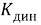
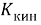
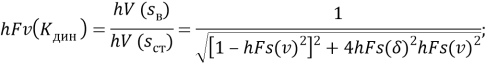
(5)

где амплитуды перемещений:

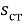

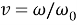
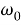
Для всех величин у (5) необходимо определить их ГВ характеристики, то есть и сами критерии
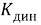
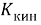
Обобщенная схема тепловых потоков в РЭС приведена на рис.1.
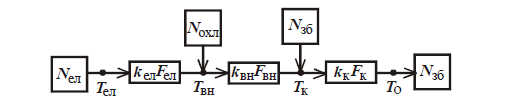
Рис. 1. Схема тепловых потоков в РЭС
Частный критерий, характеризующий тепловой режим РЭС:
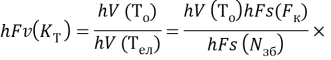
(6)
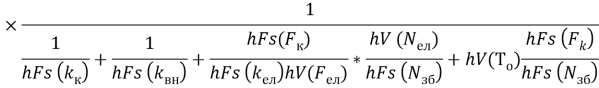
Вследствие ГВ свойств всех величин, вошедших в выражение (7), критерий

Использования частных критериев для определения характеристик конструкции при проектировании
На начальных этапах проектирования конструкции РЭС (на этапе технического предложения) из выражений частных или параметрических критериев всегда можно определить требования к отдельным параметров будущей конструкции, а также и к методам достижения требуемого значения соответствующего параметра. Ниже анализируются возможности оценок для параметров, дающих выражения частичных критериев.
Выражение (3) для КV во время проектирования определяет, какими должны быть:
— структурные и схемные решения для обеспечения нужного
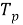
— если заданный технический ресурс
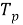
— если заданы массогабаритные параметры – элементная база и технология для обеспечения необходимого
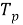
Вибрационные и ударные воздействия, при которых должен эксплуатироваться будущий РЭС, задаются в ТЗ, что и определяет требования к системе виброударозащиты, как значение критериев эффективности
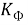
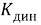
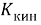
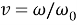
Температура
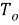

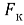
Заключение. Выражения для ЦФ в виде системы критериальных уравнений, созданные методами теории подобия, отражающих в этом комплексном показателе влияние не только параметров энергетических, механических и тепловых процессов, протекающих в РЭС, но и свойства его конструктивных элементов, что дает возможность в процессе проектирования достичь высочайшего уровня качества оптимизацией влиятельных параметров устройства. ГВ характеристики всех единичных и частных критериев, которые входят в комплексный — ЦФ — позволяют из множества полученных как результат проектирования возможных вариантов конструкции выбрать такой, характеристики которого наиболее полно соответствуют требованиям ТЗ. Комплексный показатель РЭС в форме системы критериальных уравнений, а также выражения единичных и частных критериев дают возможность создать на их основе программные модули и использовать последние в САПР оптимальных конструкций РЭА.
Литература:
- Горбань И. И. Представление физических явлений гиперслучайными моделями//Математичні машини і системи. — 2007. — № 1. — с. 34–41.
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Т1. М.: Наука, 1988. — 512 с.
- Седов Л. И. Методы подобия и размерности в механике. М.: Наука. 1987.– 432с.
- Бабаков И. М. Теория колебаний. М.: Наука. — 1968. — 560 с.







