В данной работе проанализирована актуальность методов машинного обучения для решения задач классификации, определены понятия машинного обучения, нейронной сети. Выявлена необходимая информация для анализа машинного обучения. Определены понятия классификатора Байеса, классификатора k-ближайших соседей, как результат сравнения при прогнозировании нейронной сети с 2 методами, реализованы 3 части данной работы по методам машинного обучения для решения задач классификации.
Ключевые слова: машинное обучение, нейронная сеть, классификатор метода Байеса, классификатор метода k-ближайших соседей, тренировочный набор данных, рекуррентная нейронная сеть .
В данной работе будет рассмотрена проблема применения методов машинного обучения для решения задач классификации, а также возможный подход к её решению. Машинное обучение — это большой подраздел, входящий в сферу изучения искусственного интеллекта, который исследует область методов создания алгоритмов, для обучения [1, с. 152]. Таким образом, задачей стало созданием нейронной сети, которая при помощи машинного обучения смогла бы определять типаж человека по его социальной странице из сети ВКонтакте [2, с. 68].
Для решения данной проблемы использовалась искусственная нейронная сеть с рекуррентной связью, которая представляет собой модель, где все связи направлены от входных нейронов к выходным, а от выходных к началу [3, с. 144]. Такой выбор вида нейронной сети был сделан ввиду наличия небольшого набора данных для обучения. Данная нейронная модель будет обучаться по принципу обучения с учителем, в котором используется набор из тренировочных данных [4, с. 128].
В процессе работы первым необходимым пунктом стало создание тренировочных данных в виде объектов, а также появилась необходимость в разных типах признаков данных объектов для классификации пользователей социальной сети [5, с. 231]. Поэтому в данной случае был реализован специальный Data set являющимся для нейронной сети основным потоком для обучения, который будет состоять из признаковых векторов которые имеют 14 признаков такие как: пол, города России, разговорные языки, обучение в университете, на какой форме обучения находится, научная степень, профессии в России и другие, состоит из 9 классов а именно: любопытствующий, певец, неразлучные с интернетом, много-друг, новичок, таггер, загрузчик, геймер, оратор и всё это на 5000 объектов определяющие типаж человека. Для кодирования всех признаков использовались вещественные числа с плавающей точкой, поскольку нейронная сеть может воспринимать информацию в виде разных типов чисел [6, с. 56].
После тестирования и обучения созданной нейронной сети были получены следующие результаты, где сравниваются общие потери с потерями при эпохах. Первые результаты будут приведены на рис. 1.
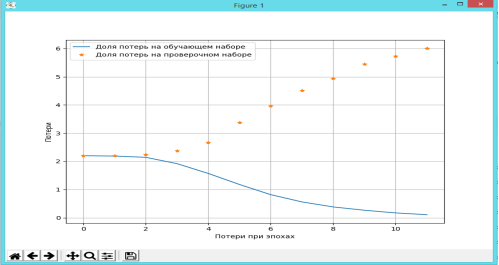
Рис. 1. График зависимости между общими потерями и потерями при эпохах
На данном графике можно увидеть, что характер поведения доли потерь на обучающем наборе ведёт себя убывающим образом, то есть ведёт к уменьшению потерь что в свою очередь является хорошим признаком, так как это способствует эффективному обучению в плане правильных ответов на каждом этапе эпохи. Доля потерь на проверочном наборе ведёт себя очень предсказуемым образом, говоря о том, что период переобучения для данной модели скоро настанет что является не хорошим признаком и означает что нейронной сети достаточно количества эпох для обучения при таком наборе тренировочных данных.
Далее на следующих этапе нейронной сетью были получены следующие результаты, где нейронная сеть при обучении получает доли правильных ответов на рис. 2.
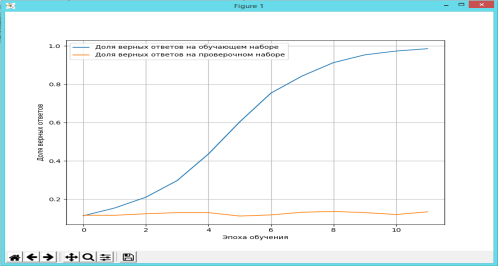
Рис. 2. График зависимости части верных ответов и доля верных ответов при эпохах обучения
Анализируя построенный график рис. 2, можно сказать, что доля верных ответов успешно возрастает, но только лишь до 12 эпохи, достигая своего пика или же максимума, после этого данный результат будет постоянным на всех эпохах, что в дальнейшем приведёт к переобучению [7, с. 319]. Что касается доли верных ответов на проверочном наборе, то тут ситуация следующая: величина получается равной в среднем 0,12. Это говорит о том, что из проверочного набора данных нейронная сеть обучилась лишь на 12 %, а остальная часть обусловлена обучением на тренировочных данных и значение, которое получилось в результате, составляет 0,90 которое условно равно 90 %. Полученный итог обучения является очень успешным для нейронной сети. Но возможно для другого набора данных может получиться обратная ситуация: преждевременное переобучение нейронной сети.
Проделав несколько полных циклов обучения, нейронная сеть смогла правильно определить, к какому из подготовленных классов пользователей социальной сети принадлежит человек по его анкете в социальной сети ВКонтакте при помощи взятых за основу признаков, которые были уже описаны выше. На рис. 3 показаны результаты обучения нейронной сети.


Рис. 3. Вывод результатов обучения нейронной сетью
Из представленных на рис. 3 результатов можно сделать вывод, что нейронная сеть при итоговом значении в 0.9 определила, что при определённом наборе классов данный человек из социальной сети относится к типу «Геймер». И этот ответ является совершенно правильным, не смотря на то, какие недостатки и потери данный были выявлены при обучении модели.
Следующий пунктом в решении поставленной проблемы станет создание классификаторов метода наивного Байеса и метода k-ближайших соседей [8, с. 163]. Начнём с рассмотрения алгоритма наивного Байеса метода. В первую очередь нужно понимать, что наивный байесовский классификатор — это несложный основанный на вероятностях классификатор, созданный на основе теоремы Байеса с доказанными предположениями о независимости [9, с. 135]. Набор данных для анализа и классификации остался прежним для этого метода: 14 признаков на 5000 объектов с 9 классами.
В результате расчётов, анализа, и прогнозирования метода наивного Байеса по нашему набору данных получается результат, изображённый на рис. 4.

Рис. 4. Вывод результата наивного байесовского классификатора
Данный метод обеспечил итоговую точность в 100.0 %. Это означает, что при определённом наборе классов данный человек будет относится в социальной сети к типу «Оратор (хочет стать популярным)».
Теперь нам необходимо рассмотреть следующий классификатор метода k-ближайших соседей, который из себя представляет метрический алгоритм для автоматической классификации объектов. Для обучения классификатора необходимо иметь набор объектов, для которых заранее определены классы. Поэтому были сделаны изменения в наборе тренировочных данных из 5000 объектов: 4500 объектов будут в рядах train, а остальные 500 объектов содержатся в рядах test. Такое решение было сделано для того, чтобы у каждого из 9 классов было равное количество объектов. В итоге получается 90 % тренировочные данные и 10 % тестовые данные.
В результате расчётов, анализа, и прогнозирования метода k-ближайших соседей по нашему набору данных получается следующий результат, изображённый на рис. 5.

Рис. 5. Вывод результата классификатора k-ближайших соседей
Из прогнозированного и проанализированного результата можно сказать, что данный метод получил итоговую точность в 20,08 %, это значение не позволяет определить из определённого набора классов данного человека по его странице в социальных сетях. Точность расчёта данного метода при общем наборе данных получился не очень хорошим, это означает что для подобного рода задачи такой метод не подходит.
В результате работы выяснилось, что при анализе, расчёте, обучении и при использовании общего набора данных метод классификатора наивного Байеса получил наилучший показатель точности, составляющий 100.0 % что классифицируемы объект относится к классу «Оратор». Нейронная сеть показала хороший результат со значением точности 90.88 % (класс «Геймер»), но результат оказался не самым точным, а значит есть смысл доработать или пересмотреть модель обучения для нейронной сети для улучшения обучения и точности результатов. Классификатор k-ближайших соседей при данной задаче показал самую маленькую точность, поэтому считаем, что такой метод не подходит для данной задачи.
Литература:
- Шолле, Ф. Глубокое обучение на Python. — СПб.: Питер, 2018. — 400 с.
- Вьюгин, В. В. Математические основы теории машинного обучения и прогнозирования М.: 2013. — 387 с.
- Бринк Х., Ричардс Дж., Феверолф М. Машинное обучение. — СПб.: Питер, 2017. — 336 с.
- Шарден Б., Массарон Л., Боскетти А. Крупномасштабное машинное обучение вместе с Python / пер. с анг. А. В. Логунова. — М.: ДМК Пресс, 2018. — 358 с.
- Рашка, С. Python и машинное обучение / пре. с англ. А. В. Логунова. — М.: ДМК Пресс 2017. — 418 с.
- Флах, П. Машинное обучение. Наука и искусство построения алгоритмов, которые извлекают знания из данных / пер. с англ. А. А. Слинкина. — М.: ДМК Пресс, 2015. — 400 с.
- Гудфеллоу Я., Бенджио И., Курвилль А. Глубокое обучение / пер. с англ. А. А. Слинкина. — 2-е изд., испр. — М.: ДМК Пресс, 2018. — 652 с.
- Траск, Э. Грокаем глубокое обучение. — СПб.: Питер, 2019. — 352 с.
- Николенко С., Кадурин А., Архангельская Е. Глубокое обучение. — СПб.: Питер, 2018. — 480 с.







