Надёжность — свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных условиях применения, технического обслуживания, хранения и транспортирования. В данной статье проведена оценка надежности основания гравитационного типа (ОГТ) платформы «Беркут» на постепенный отказ. Получены диаграммы распределения деформации в конструкции в соответствии с деформационными критериями. Проведена вероятностная оценка риска эксплуатации платформы за весь срок службы и предложены рекомендации по оценке надежности и риска морских шельфовых сооружений в ледовых условиях.
Ключевые слова: надежность, постепенный отказ, шельфовые сооружения, ледовая абразия, бетон, численное моделирование, вероятностные распределения.
Характеристики ОГТ «Беркут»
Объектом исследования является погружная платформа «Беркут» (проект «Сахалин-1»). Платформа представляет собой основание гравитационного типа, состоящее из кессона и установленных на нем четырех колонн, а также стальное верхнее строение (ВСП) (рис. 1). Кессон снабжен юбкой для заглубления в грунт.
Платформа находится на северо-восточном шельфе о. Сахалин в западно-центральной лицензированной площади Аркутун-Даги на расстоянии приблизительно 25 км к востоку от берега.

Рис. 1. Общий вид платформы «Беркут»
Опорное основание платформы «Беркут» рассчитано на установку ВСП массой до 53 000 т. Опорное основание имеет габариты:
— Высота 54.7 м;
— Ширина 100.0 м;
— Длина 132.6 м;
— Высота кессона 13.4 м;
— Высота юбки 1.4 м.
Железобетонное ОГТ платформы «Беркут» является сооружением, возведенным насухо в строительном доке. Оно представляет собой монолитную предварительно напряженную железобетонную конструкцию в виде кессона и колонны с натяжением пучков тросов «на бетон». Кессон состоит из плоской нижней плиты, наружных и внутренних стен, а также верхней плоской плиты.
Колонны цилиндрические, имеют толщину 850 мм, однако для обеспечения промежутков между колоннами, требуемых для прохода баржи (на этих участках стен толщина принята 900 мм) при осуществлении операции надвига ВСП на плаву, колонны в определенных зонах имеют овальное очертание. Колонны вертикальные с постоянной толщиной по высоте, за исключением ледового пояса и узлов крепления ВСП.
В нижней части кессона установлена система перекрещивающихся стальных юбок, заделанных в нижнюю плиту и заглубленных в грунт дна за счет собственного веса ОГТ.
Размер основных частей ОГТ:
— Толщина нижней плиты кессона 700 мм;
— Толщина нижней плиты кессона под колоннами 1050 мм;
— Толщина наружных стен кессона 650 мм;
— Толщин внутренних стен отсеков кессона 400–500–650 мм;
— Толщина верхней плиты кессона 700–850 мм;
— Высота ледового пояса 7м;
— Типовой внутренний радиус колонн 11950 мм.
Нижняя плита кессона выполнена из бетона В50 по NS 3473; верхняя плита кессона — бетон W16 F100 по ГОСТ 26633; наружные и внутренние стены кессона — бетон W16 F100 по ГОСТ 26633; колонны — бетон В70 по NS 3473, W12 F500 по ГОСТ 26633. Класс ненапрягаемой арматуры — В500NC; класс напрягаемой арматуры — канаты 1860 [4].
Аналитическое определение усилий в сооружении
Расчет будет выполняться для четырех высот колонны при разных углах приложения нагрузки.
Для аналитического определения собственных — кольцевых напряжений, возникающих от собственного веса колонны платформы Беркут (напряжений в колонне достаточно) используем формулу (1)
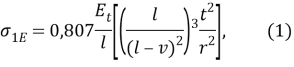
где E — модуль упругости бетона; v — коэффициент Пуассона; t — толщина стенки колонны; r — средний радиус колонны; l –высота колонны.
![Пример разбивки колонны по высоте для определения внутренних усилий [3]](https://moluch.ru/blmcbn/81180/81180.003.png)
Рис. 2. Пример разбивки колонны по высоте для определения внутренних усилий [3]
Согласно рекомендациям пособия [2], напряжения от внешней сжимающей ледовой нагрузке определяются по формуле (2):
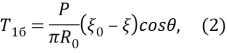
где нижний индекс 1б говорит о том, что формула принята по безмоментной теории; P — ледовая нагрузка (МПа), принимается вероятностно через полученный генератор в MS Excel по среднему и стандартному отклонению; R 0 — радиус колонны, м; cosϴ — угол приложения нагрузки, также задается вероятностно через генератор в MS Excel, а именно как разность случайного числа поворота от 0 д 360 и принятого расчетного угла приложения нагрузки; ξ 0 — высота колонны, м; ξ — высота приложения нагрузки м.
Значение напряжений от гидростатического давления воды принимается по формуле (3):
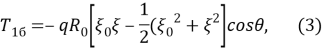
где
q
— величина плотности морской воды, не зависящая от высотной отметки;
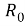
Расчет генератора напряжения в точке в MS Excel
Вероятностный расчет ледовой нагрузки производится по СП [6].
Нагрузки от воздействия движущихся ледяных полей на сооружения с вертикальной передней гранью необходимо определять: н а отдельно стоящую опору с передей гранью в виде треугольника, многогранника или цилиндрического очертания Fс,p, МН, по формуле (4):
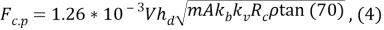
где V — скорость движения ледяного поля, м/c задается вероятностно через генератор; h d — обеспеченная толщина ровного льда, задается вероятностно через генератор; m — коэффициент формы, воспринимающей нагрузку передней грани опоры в плане, принимаемый по таблице равным 0.83 [6]; А — максимальная площадь ледяного поля, м 2 , задается вероятностно через генератор; R c — прочность льда на сжатие, МПа, задается вероятностно через генератор; K b — коэффициент, принимаемый по таблице 18 [6], задается вероятностно через генератор; K v –коэффициент, принимаемый по таблице 19 [6], задается вероятностно через генератор, ρ — плотность воды кг/м 3 , принимается 1020; Ƴ — половина угла заострения передней грани опоры в плане на уровне действия льда, град; для полуциркульного очертания необходимо принимать равным 70 градусам.
Таблица 1
Исходные параметры для вероятностного расчёта генератора по результатам полученных распределений
|
№ |
Наименование параметра |
Закон распределения |
Среднее, µ |
Стандартное отклонение, σ |
|
1 |
Скорость ледового поля |
Нормальный закон |
0,768 |
0,33855 |
|
2 |
Толщина ледового поля |
Нормальный закон |
0,95 |
0,44 |
|
3 |
Прочность льда |
Нормальный закон |
5,54 |
2,88 |
|
4 |
Площадь ледового поля |
Экспоненциальный закон |
293,36 |
470,53 |
Далее рассчитываем величину нагрузки по формуле (5):
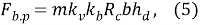
где b — протяжённость контакта ледяного поля с сооружением, принимается 11.95м. Из формул (4) и (5) принимаем величину нагрузки наименьшей.
Коэффициент деградации
По результатам натурных испытаний средняя прочность на сжатие образцов бетонных кубиков в 28-дневный период составляет 80 МПа. По графику, изображенному на рис. 3, будем принимать коэффициент деградации бетона в течение двухсот лет эксплуатации.
![График деградации бетонного камня [7]](https://moluch.ru/blmcbn/81180/81180.009.png)
Рис. 3. График деградации бетонного камня [7]
Процент потери прочности бетона во времени приведен в таблице 2.
Таблица 2
Процент потери от исходной прочности бетона
|
Прочность |
|||||||||||
|
µ |
-80 |
-78,4 |
-69,6 |
-64 |
-57,6 |
-55,2 |
-49,6 |
-47,2 |
-40 |
-38 |
-32 |
|
σ |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
|
Процент износа |
100 % |
98 % |
87 % |
80 % |
72 % |
69 % |
62 % |
59 % |
50 % |
45 % |
40 % |
В MS Excel рассчитываются параметры распределения напряжений в точке в зависимости от прочности по нормальному закону (таблица 3).
Таблица 3
Пример расчета параметров для графиков
|
Напряжения |
Вероятность точка1 |
Вероятность точка2 |
Вероятность точка3 |
Вероятность точка4 |
|
-100 |
3,61129E-07 |
6,09464E-07 |
9,95451E-09 |
5,755E-12 |
|
-95 |
3,61129E-07 |
1,65771E-06 |
4,1109E-08 |
5,0147E-11 |
|
-90 |
3,61128E-07 |
4,2841E-06 |
1,57891E-07 |
3,9114E-10 |
В таблице 4 приводится пример расчета параметров для построения графика зависимости с учетом потери прочности бетона во времени от напряжений в точке.
Таблица 4
Пример расчета зависимости напряжений от прочности
|
20 лет |
40 лет |
60 лет |
80 лет |
100 лет |
120 лет |
140 лет |
160 лет |
|
0,002488281 |
0,0001476 |
1,487E-05 |
6,717E-07 |
1,846E-07 |
6,87E-09 |
1,48916E-09 |
1,489E-09 |
|
0,008089804 |
0,0008262 |
0,0001176 |
7,886E-06 |
2,513E-06 |
1,321E-07 |
3,322E-08 |
3,322E-08 |
|
0,019316794 |
0,0033964 |
0,000683 |
6,799E-05 |
2,512E-05 |
1,867E-06 |
5,44272E-07 |
5,443E-07 |
Из полученных рядов напряжений находим среднеквадратическое отклонение и математическое ожидание в каждой и через уравнение связи [5] считаем вероятность наступления отказа по формуле (6):
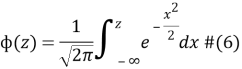
Для упрощения работы будем использовать справочные таблицы нормированного нормального распределения. Вероятность наступления отказа будет определяться как (1-z).
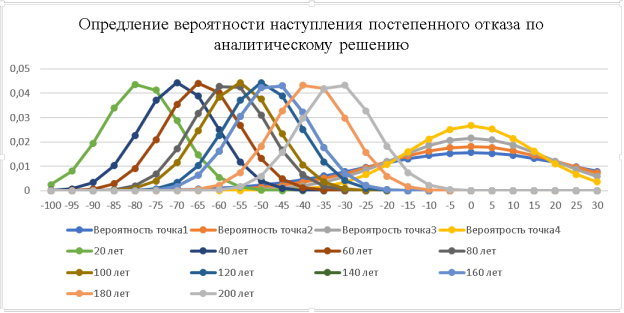
Рис. 4. Определение вероятности наступления постепенного отказа
По результатам графика видно, что уже через 120 лет эксплуатации вероятность отказа в первой точке составит 0,035; во второй — 0,019; в третей — 0,0086; в четвертой — 0,0024. По истечению 200 лет происходит отказ сооружения.
Расчет напряжений в программном комлексе ANSYS
Выполнение расчетов в программном комплексе ANSYS по условиям, которые выполнялись при аналитическом решении, является задачей сложной и непрактичной, так как для этого потребуется также вероятностно задавать ряд нагрузки из десяти тысяч значений в расчет программы.
Для упрощения получения приближенных результатов, как и при аналитическом решении, когда на разных высотах при разном направлении румба прикладывалась нагрузка, и получения вероятностного ряда напряжений, нагрузка величиной 100 МН, задавалась на высоте 10 метров от верха колонны, и величиной 250 МН, задавалась на высоте 40 метров от верха колонны.
В местах вероятного появления максимальных нпаряжений, в зоне стыка колонны и кессона со стороны действия нагрузки, были выбраны двадцать восемь узлов (рис. 5).
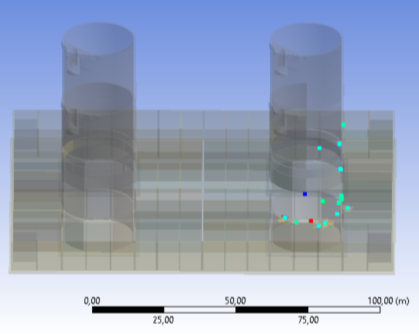
Рис. 5. Расчетные узлы
В результате было получено пятьдесят значений нагрузки и по таким параметрам как, математическое ожидание и среднеквадратическое отклонение, восстановили ряд по нормальному закону распределения. Согласованность ряда проверили в программном комплексе Statistica по критерию Пирсона (рис. 6).
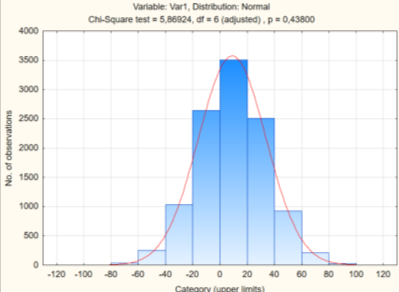
Рис. 6. Подгонка распределения напряжений
По результатам расчета при прочности бетона в 80 МН, вероятность отказа составила 0,000336.
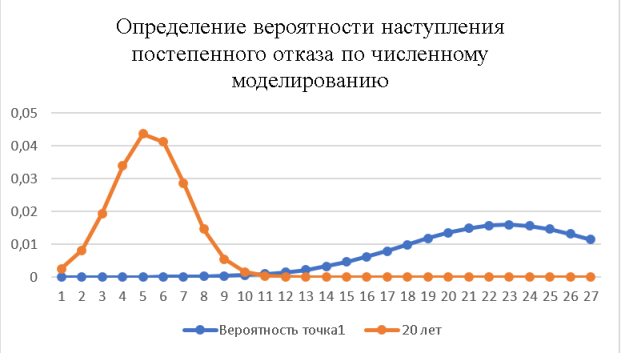
Рис. 7. Определение вероятности наступления отказа
Заключение
В статье был приведен пример оценки надежности на возникновение постепенного отказа ОГТ «Беркут» аналитическим методом при помощи расчета вероятностного генератора в программном комплексе MS Excel и выполнен расчет оценки надежности в программном комплексе ANSYS.
При расчете через генератор диапазон значений «z», при расчете которого определяется вероятность наступления отказа, составил интервал от 3 до 4. При численном моделировании приведенная величина «z» составила — 3.4. Данное значение величин описывают малое значение вероятности наступления отказа, что говорит о возможной правильности расчета, ведь значения действия внешней ледовой нагрузки задавались средние от максимальной расчетной.
По результатам графика из аналитического расчета видно, что уже через 120 лет эксплуатации вероятность отказа в первой точке составит 0,035; во второй — 0,019; в третей — 0,0086; в четвертой — 0,0024. По истечению 200 лет происходит отказ сооружения.
Литература:
- Общество с ограниченной ответственностью «Научно-производственное объединение «Гидротекс». Протокол испытаний № 48/07 от 04 декабря 2010 года, № 48/06 от 04 декабря 2010 года, № 48/05 от 04 декабря 2010 года, № 48/04 от 04 декабря 2010 года, № 48/03 от 04 декабря 2010 года, № 48/02 от 04 декабря 2010 года, № 48/01 от 04 декабря 2010 года, № 45/04 от 11 ноября 2010 года, № 45/03 от 11 ноября 2010 года, № 45/02 от 11 ноября 2010 года, № 45/01 от 11 ноября 2010 года, № 37/05 от 14 сентября 2010 года, № 37/04 от 14 сентября 2010 года, № 37/03 от 14 сентября 2010 года, № 37/02 от 14 сентября 2010 года, № 37/0. от 14 сентября 2010 года .
- Железобетонные конструкции. Специальный курс; издание 3-е, переработанное под редакцией В. Н. Байкова;1981 г.
- Design of Offshore Structure, 2000 Edited by Ivar Holand, Ove T. Gudmestad and Erik Jersin.
- Миронов М. Е. Буровая платформа «Беркут» проектирование, изготовление и установка основания. СПб — 2015 г.
- Капур К., Ламберсон Л. Надежность и проектирование систем. Мир, 1980. — 604 с. Пер. с англ. Коваленко Е. Г., под ред. Ушакова И. А.
- СП 38.13330.2018 Нагрузки и воздействия на гидротехнические сооружения (волновые, ледовые и от судов).
- Методическое пособие по назначению срока службы бетонных и железобетонных конструкций с учетом воздействия среды эксплуатации на их жизненный цикл. Москва 2019г. Министерство строительства и жилищно-коммунального хозяйства Российской Федерации Федеральное автономное учреждение «Федеральный центр нормирования, стандартизации и технической оценки соответствия в строительстве»







