В статье рассматривается моделирование работы агрегатора «Яндекс. Такси» в программном пакете Matlab.Simulink. Наглядно показано случайное распределение заявок в течение будних дней, структурная схема генератора случайных заявок, амплитудно-частотная характеристика и подсистема «Яндекс. Такси» как системы массового обслуживания.
Ключевые слова: математическая модель, агрегаторы, моделирование агрегатора «Яндекс. Такси», программный пакет Matlab.Simulink, амплитудно-частотная характеристика, схема математической модели «Яндекс. Такси».
С развитием интернета, сотовой связи и мобильных устройств начали появляться агрегаторы такси (лат. aggregation , что означает «накопление»). Агрегаторы объединили таксопарки и выстроили единый тариф оплаты, каждый в своей сети. По своей сути, агрегаторы — это разработчики программного обеспечения, приложение которых связывает водителя и пассажира, а за счет широких рекламных возможностей потенциальный пассажир знает, что заказ такси через приложение — это удобно, надежно, комфортно и безопасно, а также пассажир может сам выбрать наиболее интересное для себя предложение поездки [1].
В современных реалиях распределение заказов в агрегаторах такси происходит с использованием новейших компьютерных технологий, таких как: системы глобального позиционирования, адаптивного поиска свободных машин на основе алгоритмов искусственных нейронных сетей (учитывается пропускная способность автомобильных дорог в различных районах мегаполиса, и траектория маршрута выбирается наиболее эффективным образом). В современной экономике наблюдаются изменения экономических формаций и происходит переход к новой парадигме пассажирских перевозок. Помимо развития алгоритмов искусственного интеллекта, в настоящее время особое внимание уделяется математическому разделу теории массового обслуживания [2].
Рассмотрим моделирование работы агрегатора «Яндекс. Такси» в г.Уфа Республики Башкортостан. Наше исследование показало, что процесс формирования заявок, в общем случае, имеет стохастический характер. Так же, как и в распределении транспортного потока во времени, количество заявок, поданных на вход СМО (системы массового обслуживания), зависит от времени суток. Так, на рис. 1 показано случайное распределение заявок в течение будних дней.
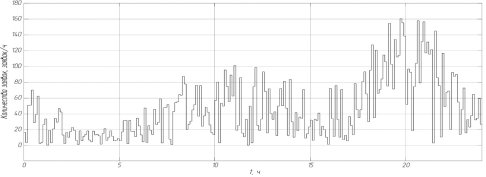
Рис.1. Случайное распределение заявок в течение будних дней
Из рис. 1 видно, что спрос на услуги «Яндекс. Такси» в вечерние часы максимален. Для дальнейшего моделирования создадим генератор случайных заявок в программном пакете Matlab.Simulink.
На рис. 2 показан построенный генератор случайных заявок. На вход генератора случайных заявок поступает набор случайных чисел, лежащих в диапазоне от 0 до 5. В зависимости от времени суток при помощи мультиплексора ( multiport switch) и весовых коэффициентов Gain 1 Gain 24 генерируется кривая в полном соответствии с кривой, показанной на рис. 2. На вход In2 поступает сигнал со счетчика часов. В дальнейшем полученный генератор случайных заявок будем рассматривать как подсистему ( subsystem ), имеющую два входа и один выход.
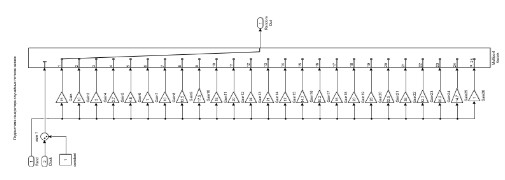
Рис. 2. Структурная схема генератора случайных заявок
Систему «Яндекс. Такси», как элемент системы массового обслуживания, будем рассматривать как апериодическое звено первого порядка, так же, как и в случае моделирования транспортных потоков. Однако в данной системе будут присутствовать такие параметры, как абсолютная пропускная способность каналов обслуживания R и производительность канала обслуживания T. Структурная схема «Яндекс. Такси» как элемента СМО, представлена на рис. 3.
Из рис. 3 можно сделать вывод, что система «Яндекс. Такси» имеет отрицательную обратную связь, что позволяет говорить о саморегулирующейся автоматической системе. На вход In1 полученной системы подается стохастический поток заявок с генератора случайных заявок (рис. 2).
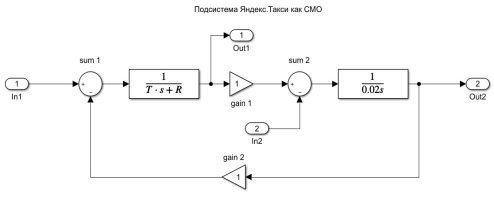
Рис. 3. Подсистема «Яндекс. Такси» как СМО
На вход In 2 поступает фактический транспортный поток. Так как фактический транспортный поток поступает в сумматор sum2 с отрицанием, то количество автомобилей в таксопарке будет уменьшаться. То есть, автомобили, находящиеся в заторе, не могут обслуживать заказы. В этом случае система может работать с перегрузкой, особенно в вечерние часы, так как имеет место повышенный спрос и повышенная загруженность автомобильных дорог города.
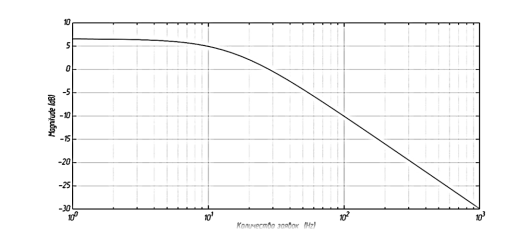
Рис. 4. Амплитудно-частотная характеристика системы «Яндекс. Такси»
Для анализа устойчивости данной системы массового обслуживания построим амплитудно-частотную характеристику разомкнутой системы (далее по тексту АЧХ). На рис. 4 показана амплитудно-частотная характеристика математической модели.
Фактически амплитудно-частотная характеристика в данном случае показывает, какое количество входящих заявок в единицу времени способна обслуживать система. Предельное значение заявок, при котором график АЧХ снижается на уровень -3 dB, будем называть критическим потоком заявок. График АЧХ зависит от основных параметров, введенных в систему «Яндекс. Такси» (абсолютная пропускная способность и производительность канала обслуживания).
Для значений R = 0,47 и T = 50 e –4 критический поток заявок будет равен 10 автомобилей в секунду.
Структурную схему системы «Яндекс. Такси» также объединим в подсистему и представим обобщенно в виде математической модели на рис. 5.
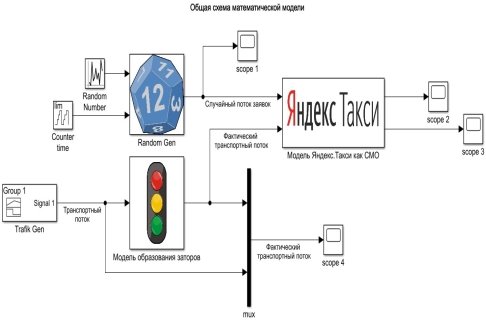
Рис. 5. Обобщенная структурная схема математической модели «Яндекс. Такси»
Таким образом, передаточная функция системы «Яндекс. Такси» была проанализирована в частотной области, что позволило построить амплитудно-частотную характеристику и определить критический поток заявок, при котором производительность системы снижается в e раз. Согласно предложенной математической модели, критический поток заявок зависит от абсолютной пропускной способности системы массового обслуживания и производительности каналов обслуживания.
Литература:
- Введение в математическое моделирование транспортных потоков / Под ред. А. В. Гасникова. — М.: МЦНМО, 2013. — 26–36 с.
- Ханчин А. Я. Работы по математической теории массового обслуживания. — М.: Либроком, 2019. — 240.







