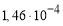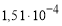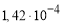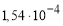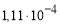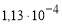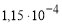В статье рассматривается возможность введения упрощенной модели балки с гофрированной стенкой при исследовании потери местной устойчивости гофра с целью минимизации времени вычисления, а так же уменьшения трудоемкости и материальных затрат при проведении натурных исследований.
Ключевые слова: местная потеря устойчивости гофра, балка с гофрированной стенкой, ANSYS, критическая сила, относительные деформации, эквивалентные напряжения.
В настоящий момент инженерная методика расчета балок с гофрированной стенкой находится на стадии разработки. Сейчас рекомендации по проектированию таких балок есть в нормах проектирования Республики Казахстан [1], но даже здесь методика разработана только для гофр треугольного очертания. Наиболее сложным и значимым при расчете гофро-балок является вопрос местной устойчивости стенки при действии локальных нагрузок. Вопросы устойчивости балки с гофрированной стенкой и методика ее обеспечения описаны в трудах А. Н. Степаненко [2, 3]. С целью дальнейшей проработки вопроса устойчивости стенок гофро-балок в данной статье рассмотрены численные эксперименты, цель которых — упростить расчетные и натурные модели.
В качестве испытываемых образцов были рассмотрены две балки. Первая балка длиной 15 м, вторая балка длиной 10 м. Размеры сечения поясов у обеих балок приняты одинаковые — 250х20 мм. Гибкости стенки взяты в диапазоне наиболее эффективного использования стенки:
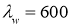

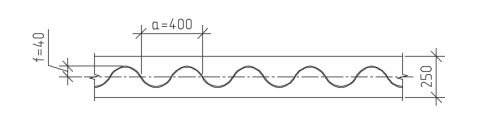
Рис. 1. Параметры гофрирования образцов балок
Расчет балок производился в программном комплексе ANSYS, расчетные модели построены с использованием конечных элементов оболочечного типа. Расчетная схема балок — балка, шарнирно опертая по двум концам. Для предотвращения общей потери устойчивости балки раскреплены в середине пролёта. Нагрузка на балку моделировалась двух видов: в первом случае нагрузка передавалась через площадку 140х40 мм, тем самом моделировалось опирание двутавра № 20, с возможным эксцентриситетом передачи нагрузки на балку, принятым в соответствии с п. 7.20 [1]. Во втором случае нагрузка распределялась по всей ширине пояса (140х250 мм). Нагрузка в образцах прикладывалась в различных по длине местах, в первом случае на расстоянии метра от опоры, во втором посередине пролета. Так же рассмотрено смещение нагрузки в пределах длины волны. Схемы приложения нагрузок представлены на рис. 2.
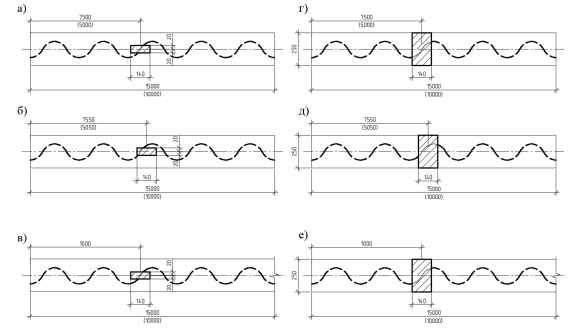
Рис. 2. Схемы приложения нагрузок: а) и г) в середине пролета; б) и д) со смещением в пределах длины волны; в) и е) на расстоянии метра от опоры
В программном комплексе ANSYS на указанные выше схемы, задавалась одинаковая нагрузка 10 кН. ПК ANSYS в качестве решения выдает «множитель нагрузки» — такое число, на которое надо умножить заданное значение нагрузки, чтобы произошла потеря устойчивости.
Значения «множителя нагрузки», полученные при испытаниях балок пролётом 15 и 10 м, сведены в таблицу 1.
Таблица 1
|
Схема приложения нагрузки по рис. 2 |
Значения “множителя нагрузки” для балки длиной 10 м |
Значения «множителя нагрузки» для балки длиной 15 м |
|
а) |
19,516 |
19,291 |
|
б) |
21,841 |
21,681 |
|
в) |
19,65 |
19,37 |
|
г) |
21,041 |
20,523 |
|
д) |
23,379 |
22,765 |
|
е) |
20,983 |
20,557 |
Важно отметить, чтобы результаты численных экспериментов были корректны, при исследовании потери местной устойчивости гофра от действия местной нагрузки на образцах большой длины, необходимо в местах приложения нагрузки уменьшить конечно-элементную сетку. В данном эксперименте в местах сгущения принята 4-х угольная конечно-элементная сетка со стороной 10 мм. Сетка уменьшалась до того момента, пока расхождение в результатах не стало меньше 5 %. Эксперимент проводился в линейной постановке, то есть без учета физической и геометрической нелинейности.
По результатам, приведенным в таблице 1, можно сделать вывод, что наиболее опасным является такое положение нагрузки, при котором нагрузка передается на монотонных участках синусоиды. В местах экстремумов за счет большой кривизны местная устойчивость стенки на действие локальных нагрузок возрастает. Так же важно отметить, что ширину приложения локальной нагрузки следует принимать в соответствии с п. 7.20 [1] см. рис. 2. При таком приложении нагрузки потеря устойчивости гофра наступает раньше, чем при приложении нагрузки через всю ширину пояса гофрированной балки.
Сравнивая результаты численных экспериментов а) и в), г) и е) можно заключить, что критическая сила потери местной устойчивости гофра не зависит от местоположения локальной нагрузки по длине балки. Первая форма потери устойчивости гофра для балки пролётом 10 м представлена на рис. 3. Для балки пролётом 15 м первая форма потери местной устойчивости аналогична.
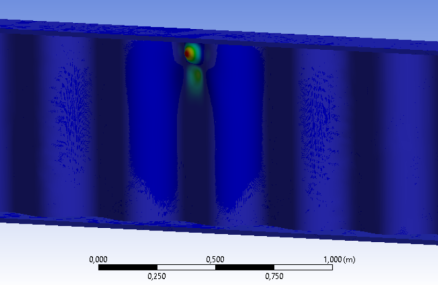
Рис. 3. Первая форма потери устойчивости гофра от действия локальной нагрузки по схеме «а»
Опираясь на вышеизложенные выводы, выдвинем гипотезу о возможности использования упрощенной модели.
В качестве упрощенной расчетной модели был рассмотрен участок балки длиной равной трем длинам волны гофра (1200 мм), все прочие параметры балок оставлены без изменений. Построение и расчет упрощённых схем был выполнен для случаев а) и г) как для наиболее опасных. Сравнение велось по трем параметрам:
— Критической силе потери устойчивости гофра (N cr 1 и N cr 2 )
— Относительным деформациям, развивающимся в образцах при нагрузке равной 10 кН ( 1 и 2 )
— Максимальным эквивалентным напряжениям в образцах при нагрузке равной 10 кН (σ 1 и σ 2 )
Результаты сравнения сведены в таблицу 2. В таблице 2, отслеживаемые факторы с индексом 1, соответствуют испытанию образца балки. А факторы с индексом 2 соответствуют упрощённой модели.
— отклонение результатов, полученных на упрощенной модели, относительно результатов полученных на образцах балках.
Таблица 2
|
Схема приложения нагрузки (рис.) |
Длина балки, м |
N cr 1 , кН |
N cr 2 , кН |
, % |
1 |
2 |
, % |
σ 1 , МПа |
σ 2 , МПа |
, % |
|
а |
10 |
195,16 |
199,06 |
2,0 |
|
|
3,4 |
29,1 |
30,17 |
3,7 |
|
а |
15 |
192,91 |
194,77 |
1,0 |
|
|
8,4 |
28,45 |
30,68 |
7,8 |
|
г |
10 |
210,41 |
212,25 |
0,9 |
|
|
1,8 |
22,18 |
22,53 |
1,6 |
|
г |
15 |
205,23 |
206,72 |
0,7 |
|
|
3,6 |
22,26 |
22,92 |
3,0 |
Анализируя результаты, полученные в ходе численного эксперимента, можно сделать вывод о том, что упрощенная модель, с достаточной степенью точности характеризует критическую силу потери устойчивости гофра. Погрешность результатов не превышает 2 %. Форма потери устойчивости, полученная на упрощенной схеме, представлена на рис. 4, совпадает с той, что получена на полноразмерной балке. Важно учесть, что 2 % отклонение не идет в запас, поэтому при разработке дальнейших методик на основе такой модели это отклонение необходимо учесть коэффициентом запаса.
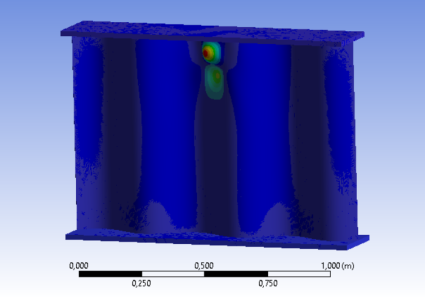
Рис. 4. Первая форма потери устойчивости гофра от действия локальной нагрузки в упрощенной модели
По результатам эксперимента видно, что погрешность при оценке относительных деформаций и эквивалентных напряжений по упрощенной схеме растет с увеличением гибкости образца, характер изополей напряжений при этом сохраняется. Картины изополей напряжений представлены на рис. 5. Так же отметим, что при передаче нагрузки через всю ширину полки сходимость результатов по всем контролируемым показателям оказывается выше.
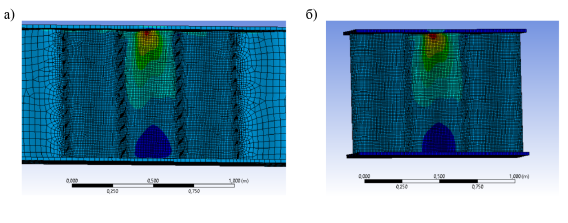
Рис. 5. Изополя эквивалентных напряжений от действия локальной нагрузки: а) в балке пролетом 10 м; б) в упрощенной модели
В заключение статьи можно сделать вывод, что при исследовании вопросов местной устойчивости стенки при действии локальной нагрузки с высокой степенью достоверности можно пользоваться упрощенной расчетной моделью, длину которой можно принять равной трем длинам волны гофры. Такой подход позволяет уменьшить расход стали при проведении лабораторных испытаний, а так же уменьшает время расчета в программных комплексах конечно-элементного анализа. Такой подход особенно актуален при решении задач с учетом физической и геометрической нелинейности, так как они требуют больших вычислительных мощностей.
Литература:
- СНиП РК 5.04–23–2002. Стальные конструкции. Нормы проектирования. — Астана, 2003. — 118 с.
- Степаненко А. Н. К вопросу общей устойчивости наклонно гофрированной тонкой стенки металлической балки//Исследование металлических конструкций с профилированными элементами сечения. Хабаровск: ХПИ, 1975. С. 29–37.
- Металлические конструкции: учебник для студентов высших учебных заведений / Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др. М.: Академия, 2006. — 688 с.