Анализ методов получения плотности распределения вероятности нарушения защищенности объекта



В ходе изучения защищенности объекта была выявлена проблема определения плотности распределения вероятности нарушения безопасности. Проблема связана с тем, что, как правило, защищенность оценивается неким числовым значением, а не значением вероятности реализации атаки. В связи с этим были определены и проанализированы наиболее подходящие способы построения математической модели для построения плотности распределения: модель полной определенности, модель погрешности и закон треугольного симметричного распределения Симпсона.

Ключевые слова : защищаемый объект, плотность распределения, нарушение безопасности.

During the study of the security of the object, a problem was identified determination of the probability distribution density security breaches. The problem is related to the fact that, as a rule security is evaluated by a certain numerical value, and not the value of the probability of implementing the attack. In this regard, the most suitable methods were identified and analyzed building a mathematical model for constructing the distribution density:the complete certainty model, error model and Simpson's law of triangular symmetric distribution.

Keywords : protected object, distribution density, security breach.

Невыполнение необходимых требований по обеспечению безопасности влечёт за собой разного рода атаки как физические, так и информационные.

В настоящее время актуальным является построение математических и концептуальных моделей в ходе анализа которых можно более подробно рассматривать любую структуру событий.

Событие — это изменение свойств объектов, при котором он переходит из одного состояния в другое.

Для построения концептуальной модели событий используется множество методов, но в данной статье будут рассмотрены:

— модель полной определенности;

— модель погрешности;

— закон Симпсона о треугольном симметричном распределении.

Модель полной определенности — модель при которой вероятность является выраженной, то есть реализация каждого из событий в структурной системе объекта имеет конкретное значение от 0 до 1.

Значение в такой модели могут быть заданы в виде таблицы, элементами которой являются значения частных критериев эффективности функционирования системы [1].

Плотностью распределения этой случайной величины является дельта-функция:

, (1)

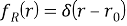
где – плотность распределения;

– вероятность реализации события;

– заданная вероятность;

– дельта функция.

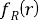
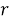
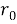
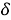
Функция распределения имеет вид ступеньки и определяется следующим образом:

, (2)

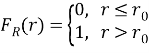
График функции распределения F(r) представлен на рисунке 1.

Рис. 1. Функция распределения модели полной определенности

Модель погрешности — модель в которой величины реализации событий задается конкретным диапазоном, края которого равноудалены от центра распределения математических ожиданий измеренных значений.

Величина диапазона, в котором распределяются вероятности, называется размахом. Центр размах совпадает с центром распределения [2].

, (3)

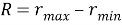
где – правая граница погрешности;

– левая граница погрешности.

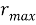
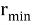
Функция распределения модели погрешности является равномерной и имеет вид:

, (4)

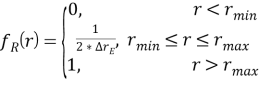
График плотности распределения F(r):

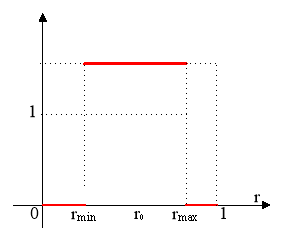
Рис. 2. График плотности распределения модели погрешности

Функция распределения в этой модели и её график имеют вид:

(5)

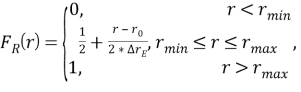
График функции распределения F(r):

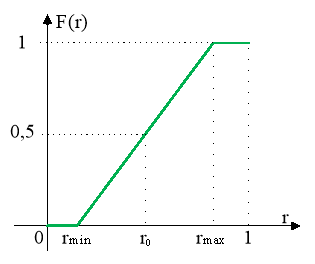
Рис. 3. График функции распределения модели погрешности

Закон Симпсона о треугольном симметричном распределении гласит о том, что симметричным является распределение, в котором частоты любых двух вариантов, расположены одинаково по отношению к центру распределения. В треугольном симметричном распределении наблюдается равенство между средней арифметической и медианой [3].

Модель вероятности реализации угрозы в симметричном распределении эквивалентна среднему значению границ диапазона.

, (6)

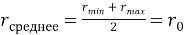
где – среднее значение диапазона;

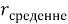
Симметричное треугольное распределение Симпсона описывается:

, (7)

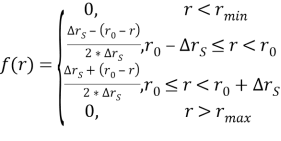
где – полуразмах распределения Симпсона.

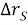
Плотность треугольного симметричного распределения имеет график следующего вида:

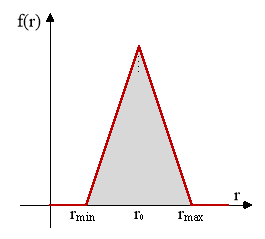
Рис. 4. График плотности треугольного симметричного распределения

Функция распределения Симпсона имеют вид:

, (8)

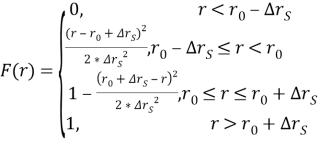
Функция распределения Симпсона имеют следующий график:

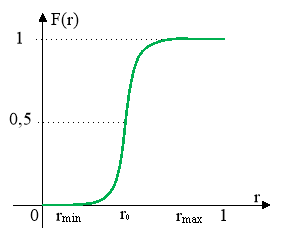
Рис. 5. Функция распределения для модели Симпсона

В результате рассмотрения методов полной определенности, погрешности и закона треугольного распределения Симпсона можно привести следующие выводы:

— в случае, когда вероятность реализации каждого из событий угрозы известна с необходимой точностью, применение метода полной определенности является наиболее предпочтительным;

— если вероятность реализации каждого события в системе угроз задавал некий «эксперт», то для данного случая больше всего подходит модель погрешности. Поскольку любая из величин представленная «экспертом» имеет погрешность в той или иной степени;

— модель треугольного симметричного распределения является частным случаем закона Симпсона и как правило почти не встречается, поскольку мнение «эксперта» склоняется в одну из сторон плотности распределения. В данном случае более эффективным будет применение общего случая распределения Симпсона.

Литература:

1. С. Цой, С. М. Цхай. Прикладная теория графов. — Алма-Ата: Наука, 1971.

2. Феллер В. Введение в теорию вероятностей и её приложения. В 2-х томах. — М.: Мир, 1984.

3. Сигорский В. П. Математический аппарат инженера. — Киев: Техника, 1975.