В статье авторы рассматривают два способа построения дисперсии Аллана: с помощью вычисления дисперсии соседних отклонений, а также исходя из спектральной плотности мощности шума.
Ключевые слова: вариация Аллана, дисперсия, ИНС, шумы, спектральная плотность мощности.
Для использования данных, полученных на выходе инерциальной навигационной системы (ИНС), необходимо произвести фильтрацию информационной составляющей от различных типов шумовых составляющих.
Для оценки шумов нестабильности показаний датчиков ИНС принято использовать метод дисперсии (вариации) Аллана — выделение семи составляющих шума измерений [1].
В данной статье рассмотрены два способа реализации построения вариации Аллана MEMS-датчика ADIS16407 и проведен их сравнительный анализ.
Первый способ реализации — метод непосредственного анализа временного процесса. Основой данного метода является анализ временных окон. Временной процесс делится на временные окна с фиксированной длительностью, которая в свою очередь выбирается произвольно, но должна быть кратна периоду выборки — величине, обратной частоте выборки датчика.
Данный способ математически описывается следующим образом [2]:
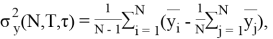
Где
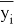
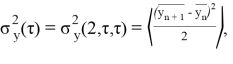
где под <…> понимается усреднение в бесконечных пределах,
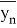
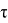
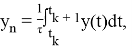
где
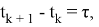
Графики вариации Аллана для некалиброванного трёхкоординатного гироскопа датчика ADIS1607, полученные по выражениям (1)-(4) для
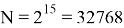
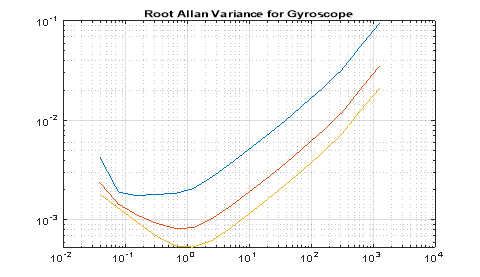
Рис. 1. Вариация Аллана для гироскопа датчика ADIS1607 по 3 осям
Второй способ реализации — построение вариации Аллана с помощью конвертации последовательности спектральной плотности мощности (СПМ) с последующим выделением корня из результата конвертации. Связь между вариацией Аллана и СПМ записывается следующим образом [1]:
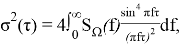
При представлении СПМ в виде дискретной последовательности:
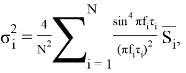
где
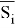
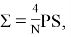
где P — вектор строка из отсчётов
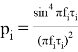
S — вектор столбец СПМ.
Посмотрим полученный график СПМ:
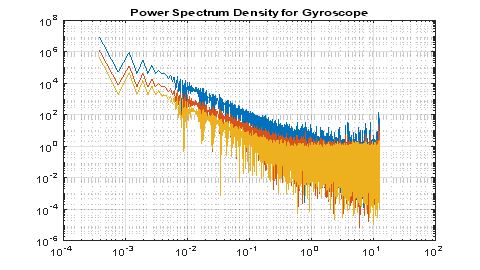
Рис. 2. Спектральная плотность мощности по 3 осям
Воспользуемся формулой (7) для реализации вариации Аллана с помощью СПМ, результат представлен на рис.3:
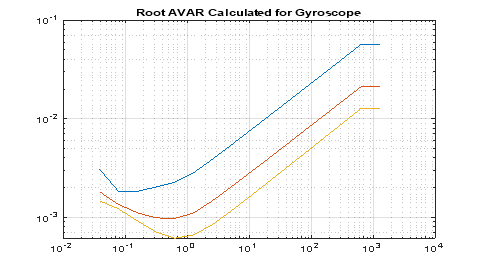
Рис. 3. Вариация Аллана для датчика ADIS1607 с помощью СПМ по 3 осям
Заметим, что полученный график схож с рис.1. Произведем коррекцию дрейфа гироскопа путём замера средних значений показаний по представительной выборке (
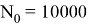
Вариация Аллана, полученная двумя вышеописанными способами для скорректированных показаний, изображена на рис.4 и рис.5.
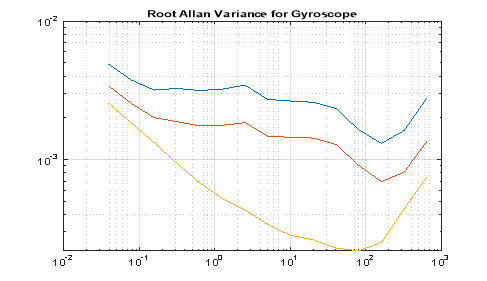
Рис. 4. Вариация Аллана для датчика ADIS1607 по 3 осям после корректировки
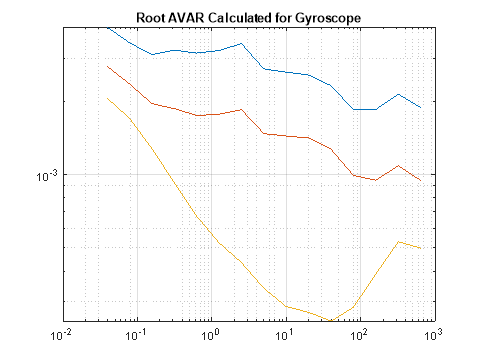
Рис. 5. Вариация Аллана после конвертации для датчика ADIS1607 с помощью СПМ по 3 осям
При сравнении графиков, полученных двумя способами, заметны отличия, связанные с конечностью выборки экспериментальных данных. Качественный характер при этом сохраняется, что подтверждает возможность определения вариации Аллана двумя способами, описанными в статье. После коррекции дрейфа датчика полученные значения вариации укладываются в данные, заявленные производителем.
Литература:
- Литвин М. А., Малюгина А. А., Миллер А. Б., Чикрин Д. Е. Типы ошибок в инерциальных навигационных системах и методы их аппроксимации. М.: Информационные процессы., Том 14, № 4., 2014. С. 326–339.
- Сирая Т. Н., Статическая интерпретация вариации Аллана как характеристики измерительных и навигационных устройств. М.: Гироскопия и навигация., Том 28 № 1, 2020 С. 3–18







