В статье приводится обзор подходов для построения систем обнаружения столкновений объектов. Приводится классификация алгоритмов по нескольким признакам.
Ключевые слова: обнаружение столкновений, ограничивающие объёмы, ограничивающая сфера, ориентированные ограничивающие рамки.
Обнаружение столкновений является неотъемлемой частью многих приложений, включая компьютерные игры, физическое моделирование, робототехнику, виртуальное прототипирование и инженерное моделирование.
В компьютерных играх обнаружение столкновений обеспечивает сохранение иллюзии твёрдого мира. Оно не даёт персонажам игроков проходить сквозь стены или проваливаться через пол.
Основной принцип обнаружения столкновений
Обнаружение столкновений чаще всего используется в физических движках, компьютерной анимации и робототехнике. Основная задача состоит в том, чтобы определить, контактируют ли два или более объектов друг с другом. При обнаружении столкновений двумя важными аспектами являются оперативность и точность.
Требования к обнаружению столкновений:
— проверка на наличие столкновения;
— позиция обнаруженного столкновения;
— расстояние между объектами;
— прогнозирование столкновения в следующий раз.
Алгоритмы обнаружения столкновений можно классифицировать по типу представления входных данных и по типу распознавания столкновений.
Рассмотрим алгоритмы, использующиеся в системах обнаружения столкновений, по типу представления объектов на входе системы. Наиболее часто встречаются входные данные следующих типов:
— сетки из треугольников;
— конструктивная блочная геометрия;
— неявно заданная геометрия.
Использование сетки из треугольников обусловлено тем, что треугольник является базовым геометрическим примитивом для отображения на экране дисплея сложных объектов. Координаты точек передаются через API (Application Programming Interface) драйверу графического адаптера, который растеризует входные данные и выводит на экран.
Конструктивная блочная геометрия часто используется в САПР (Система автоматизированного проектирования). Комбинируя простые базовые трёхмерные объекты, такие как сферы, прямоугольные параллелепипеды, конусы, на выходе получаем сложный объект.
Неявное задание объекта предполагает задание формы объекта в виде математического уравнения. Например, область, ограниченную сферой, можно задать в виде уравнения
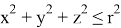
Далее, если не указано явно, предполагается, что в качестве входных данных для алгоритма обнаружения столкновений используются полигональные сетки из треугольников.
Проверка на столкновение двух объектов может быть очень сложной задачей, включающей проверки между множеством граней каждого объекта. Для быстрого выполнения этой задачи часто используются упрощенные формы для представления каждого объекта, что позволяет проводить быстрые тесты на столкновение. Эти тесты, конечно, не обладают достаточной точностью, и часто они используются в качестве быстрого теста, чтобы определить, требуется ли дальнейшее подробное тестирование.
Мы рассмотрим три таких ограничивающих объёма (рис. 1):
— ограничивающие сферы;
— ограничивающий прямоугольник, выровненный по координатным осям;
— ориентированные ограничивающие рамки;
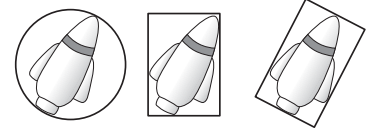
Рис. 1. Типы ограничивающих объёмов
Ограничивающая сфера используется как один из типов ограничивающего объёма при определении столкновений. При применении данного метода объект полностью находится внутри данной сферы, и столкновения рассчитываются от поверхности сферы, а не от поверхности заключенного в неё объекта (рис. 2). Использование ограничивающей сферы в обнаружениях столкновений является самым простым, быстрым и грубым методом.

Рис. 2. Ограничивающая сфера
Ограничивающая сфера — это гипотетическая сферическая часть пространства, которая полностью охватывает объект. Она задаётся трёхмерной координатой, которая определяет центр сферы, и скалярным радиусом, который определяет максимальное расстояние от центра сферы к любой точке, которая находится внутри или на поверхности объекта.
Ограничивающий прямоугольник, выровненный по координатным осям (Axis Aligned Bounding Box, AABB) — это прямоугольник, четыре стороны которого выровнены относительно системы координат, в которой он находится (рис. 3). Это значит, что прямоугольник не может вращаться и всегда находится под углом в 90 градусов (обычно выровнен относительно экрана).
AABB — очевидный и простой метод для реализации и полезен в играх, где мало объектов, которые могут столкнуться. Однако, если вы захотите реализовать эту форму обнаружения столкновений в игре, в которой присутствует огромное количество сталкивающихся объектов, этот метод станет слишком дорогостоящим в вычислительном отношении, и поэтому вам придется искать способы оптимизации этих вычислений.
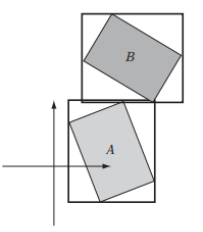
Рис. 3. Ограничивающий прямоугольник, выровненный по координатным осям
Чтобы отличить общий случай от AABB, произвольный ограничивающий прямоугольник иногда называют ориентированной ограничивающей рамкой (Oriented Bounding Box, OBB), где используется локальная система координат существующего объекта. AABB намного проще проверить на пересечение, чем OBB, но у него есть недостаток — AABB не вращается, OBB можно вращать (рис. 4). Основная идея метода заключается в использовании простой геометрии вместо сложных геометрических новинок.
Рис. 4. Ориентированные ограничивающие рамки
Заключение
Ограничивающие объемы — это простые геометрические формы, внутрь которых вписываются один или несколько объектов большей геометрической сложности. Чаще всего в качестве ограничивающих объемов используются сферы и прямоугольники. Если требуется действительно плотная посадка, можно использовать объемные плиты или выпуклые корпуса. При использовании ограничивающих объемов с более плотной посадкой вероятность преждевременного отклонения увеличивается, но в то же время тест ограничивающего объема становится более дорогим, а требования к хранилищу для ограничивающего объема возрастают. Обычно ограничивающие объемы вычисляются на этапе предварительной обработки и, при необходимости, преобразуются с помощью ограниченных объектов во время выполнения, чтобы соответствовать движениям объектов.
Литература:
- Robert Dunlop, Collision Detection: Using Bounding Spheres [Электронный ресурс]. — Режим доступа http://www.mvps.org/directx/articles/using_bounding_spheres.htm
- Raigan Burns, Mare Sheppard, Using well-known collision detection algorithms, [Электронный ресурс]. — Режим доступа http://noregret.org/tutor/n/collision/
- Christer Ericson, Real-Time Collision Detection, 2005 by Elsevier Inc. p.77–102







