В данной работе авторами представлен параллельный алгоритм быстрого преобразования Фурье, универсальным примитивом выполнения вычислений которого является семейство акторов.
Ключевые слова : модель акторов, параллельное программирование, быстрое преобразование Фурье.
Модель акторов является обобщением сетей конечных автоматов, не имеющих ограничений на глобальную синхронизацию и определенный порядок поступления сообщений, что дает новые возможности в написании параллельных программ. В основном модель используется как теоретическая база для создания параллельных систем, в частности, в настоящее время находит применение в мультиагентных системах и облачных вычислениях [1]. В виду конкурентности ( concurrency ) модели и её фундаментально отличительных концепций, интересно проследить возможность адаптаций традиционных последовательных алгоритмов под данный вид модели параллельных вычислений, а также выявить её недостатки.
Цель данной работы состоит в разработке параллельного алгоритма быстрого преобразования Фурье, путем создания подходящей топологии системы акторов и распределения вычислительных компонентов по её узлам, а также сравнительный анализ относительно последовательного аналога.
На первом этапе алгоритма происходит инициализация системы акторов — получение значений вектора коэффициентов многочлена, создание актора с поведением fft , который ответственен за вычисление быстрого преобразования Фурье, проинициализированный размером вектора, первообразными корнями из единицы, и адресом идентификатора актора, куда будет отправлен результат преобразования [2]. Затем происходит пересылка сообщения в созданный актор, инициирующая начало вычислений. Следующим этапом происходит развертывание классического алгоритма быстрого преобразования Фурье в виде двоичного дерева. Корень дерева отвечает за все компоненты коэффициентов полинома, где для всех остальных вершин, кроме листьев, каждому левому потомку соответствуют элементы, стоящие на четных местах предка, а каждому правому — на нечетных (Рис. 1). Задача для акторов поведения fft заключается в управлении и передачи необходимых параметров для инициализаций акторов с поведением merge , выполняющих пересчет DFT и слияние результатов преобразования, а также определение листовых элементов — моментов окончания создания новых акторов типа fft [3]. Для их выявления каждому актору, помимо первообразных корней и PID порождающего процесса [4], необходимо пересылать переменную, накапливающую сумму степеней двойки для правых потомков на каждой глубине дерева (Рис. 1).
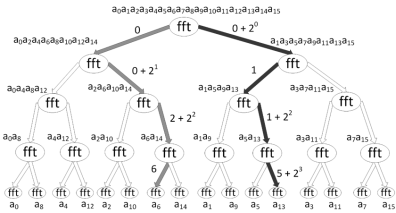
Рис. 1. Определение положения листовых элементов в векторе коэффициентов многочлена
Процессы типа merge выполняют несколько функций: они ожидают прихода двух последовательностей, производят их слияние, создают новый актор и передают ему данные для перерасчета DFT над вектором коэффициентов. При ожидании двух последовательностей, акторы реализуют простейшего рода барьерную синхронизацию [5] . Топология получившейся системы представлена на Рисунке 2.
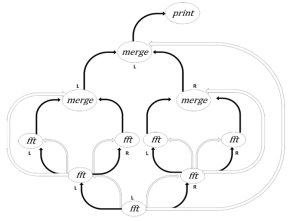
Рис. 2. Система акторов, реализующая преобразование Фурье
При подсчете получившегося ускорения алгоритма было обнаружено, что общая вычислительная сложность параллельного варианта, запущенного на множестве процессов, отличается на некоторую константу. Результат представлен на Рисунке 3. Следовательно, несмотря на разницу во времени выполнения преобразования, описанный алгоритм можно относительно легко распределить по вычислительным узлам, за счет чего можно будет погасить данную константу.
Несмотря на возможность распараллеливания алгоритма быстрого преобразования Фурье, построенная система на базе модели акторов имеет недостатки. В некоторых местах приходилось имитировать процессы итерации, при которых несколько теряется смысл данной архитектуры, т. е. описанные операции выполняются медленнее, нежели при их посредственной последовательной обработке.
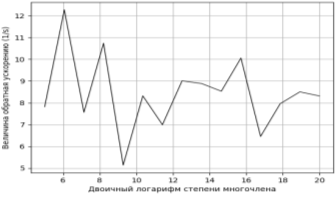
Рис. 3. Зависимость ускорения алгоритма от степени многочлена
Одним из главных недостатков является неопределенность прихода сообщений от акторов, что подталкивает на реализацию подобия барьерной синхронизации и дополнительной обработке некоторых случаев. К достоинствам можно отнести его неуязвимость к взаимным блокировкам. Поскольку процессы не имеют разделяемых данных, это избавляет от продумывания стратегий для обработки критических секций. Однако, одним из главных результатов является сохранение вычислительной сложности алгоритма и возможности его динамического масштабирования в рамках распределенной среды.
Литература:
- Федотов И. Е. Модели параллельного программирования. — М.: СОЛОНПРЕСС, 2012. 384 с.
- Быстрое преобразование Фурье. URL: https://emaxx.ru/algo/fft_multiply (дата обращения: 03.03.2021)
- Agha G. A. Actors: A Model of Concurrent Computation in Distributed Systems. — Cambridge, Massachusetts: MIT Press, 1986. — 190p.
- Clinger W. D. Foundations of Actor Semantics. — Doctoral Dissertation. — MIT Artificial Intelligence Laboratory, 1981. — 177p.
- Andrews, Gregory R. Foundations of multithreaded, parallel, and distributed programming. — Reading, Mass.: Addison-Wesley, 2000. — 664p.







