Управление движением манипулятора в пространстве координат инструмента



В статье исследуется кинематическое управление манипулятора по программному движению его инструмента. Рассматривается метод планирования траектории в пространстве обобщенных координат. Строится программная траектория движения манипулятора на основе программной траектории инструмента. Производится оценка энергетических затрат.

Ключевые слова: робот-манипулятор, обратная задача кинематики, планирование траектории, программное движение.

В связи с большим интересом к робототехнике, в настоящее время ставится и решается немало задач об управлении движением роботов-манипуляторов. Актуальность работы связана с исследованиями в области промышленной и космической робототехники, а также при разработке алгоритмов оптимального выполнения заданных операций.

Целью работы является разработка математического аппарата для оценки выполнения операции перемещения инструмента робота в пространстве рабочей зоны манипулятора.

Объектом исследования в данной работе является робот-манипулятор, кинематическая схема которого изображена на Рис.1.

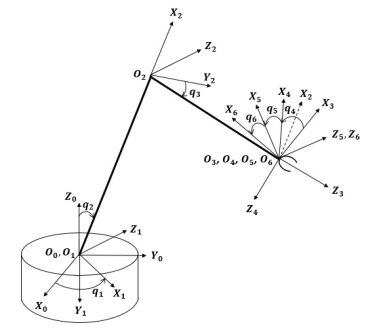
Рис. 1. Кинематическая схема робота-манипулятора

Система — система координат основания. Звено

связано с основанием шаровым шарниром. Взаимное положение основания и первого звена определяется кинематической парой 4-го класса, первого и второго звена — кинематической парой 5-го класса, второго и третьего — кинематической парой 3-го класса. Длины звеньев и заданы, постоянны и равны соответственно и . Обобщенными координатами перехода из одной системы координат в другую являются углы . Положение и ориентацию схвата будем искать в форме матрицы однородного преобразования [1]:

.

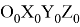
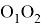
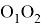
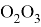
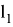
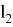
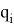
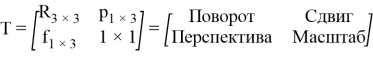
Ниже представлено решение обратной задачи о положении, полученное методом обратных преобразований [2]:

,

,

.

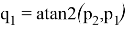
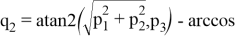
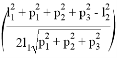
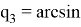
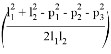
В решении обратной задачи об ориентации требуется рассмотреть несколько вариантов в зависимости от значения [3]:

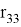
—При :

,

,

.

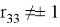
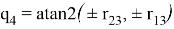
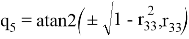
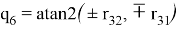
—При

,

,

.

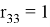
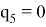
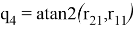
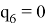
—При

,

,

.

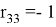
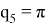
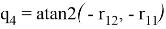
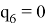
Будем считать, что границей рабочей зоны манипулятора является сфера, радиус которой равен сумме его звеньев:

.

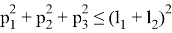
Ограничения на обобщенные координаты:

, , ,

, .

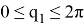
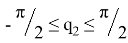
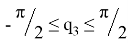
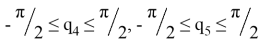
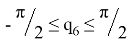
Переходя к решению задачи планирования траектории в пространстве обобщенных координат был рассмотрен режим разгона — торможения [1].

Обозначим — пространство состояний системы. Пусть в момент времени манипулятор находится в точке . Необходимо определить такую функцию , для которой в момент времени манипулятор находится в точке .

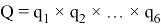
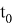
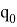
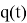
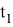
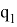
В рамках данной работы был взят следующий закон изменения :

.

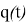
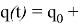
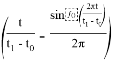
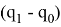
Далее рассматривается задача формирования программного движения манипулятора в пространстве координат инструмента.

Пусть — однородные матрицы положения инструмента в начальной и конечной точках:

,

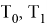
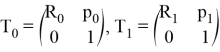
и задано время перемещения инструмента из начального положения в конечное. Требуется построить непрерывную траекторию инструмента в виде , которая обеспечивает режим разгона — торможения:

,

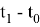
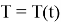
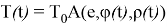
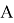
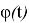
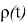
где — матрица 4×4, зависящая от параметров: e — вектор 3×1, вокруг которого осуществляется поворот инструмента, — угол поворота, — вектор переноса 3×1.

Матрица имеет ту же структуру, что и матрица . Граничные условия для элементов матрицы :

.

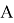
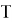
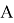
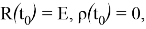
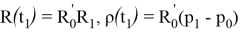
Вектор, вокруг которого осуществляется поворот, имеет вид:

, , ,

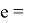
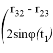
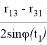
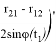
где — элементы матрицы .

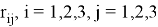
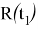
Матрица поворота ищется в форме:

,

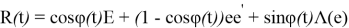
где [2].

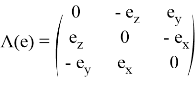
Функции и строятся из условия обеспечения режима разгона — торможения:

,

.

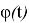
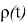
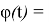
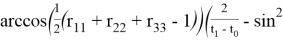
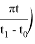
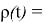
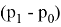
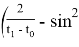
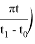
Таким образом строится , описывающая программную траекторию инструмента в декартовом пространстве и обладающая необходимыми свойствами. Используя решение обратной задачи кинематики для , можно построить программную траекторию движения манипулятора.

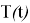
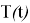
Для оценки энергетических затрат манипулятора при режиме разгона-торможения в пространстве обобщенных координат и в пространстве координат инструмента вводятся функционалы — и соотвественно. Функционал учитывает возможность наличия локальных экстремумов значения на рассматриваемом промежутке времени — .

,

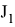
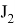
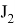
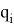
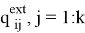
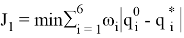
где, например, — вектор весовых коэффициентов,

— начальное положение манипулятора, — желаемое положение манипулятора.

,

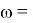
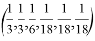
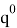
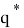
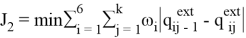
где . Если локальных экстремумов обобщенных координат нет на рассматриваемом промежутке времени, то и функционал равняется функционалу .

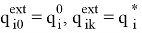
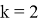
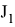
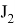
В рамках данной работы была реализована программа в прикладном пакете Matlab для оценки выполнения операции перемещения инструмента робота. Ниже представлены результаты выполнения программы на конкретном примере.

Начальные данные:

, ,

.

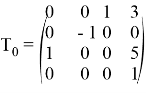
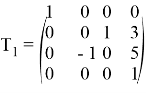
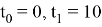
Результат выполнения программы:

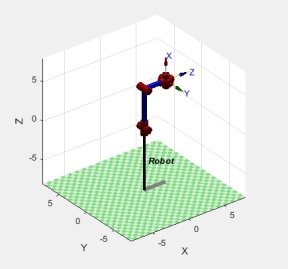
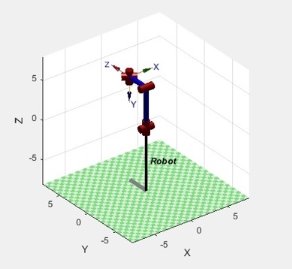
Рис. 2 Начальное положение Рис. 3 Конечное положение

Оценка энергетических затрат:

, .

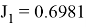
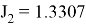
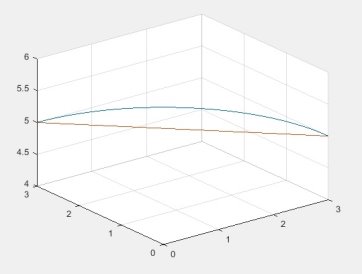
Рис. 4. Координаты полюса

Здесь и далее синим обозначены результаты, полученные при режиме разгона — торможения в пространстве обобщенных координат, а красным — в пространстве координат инструмента.

Ниже представлены графики изменения обобщенных координат.

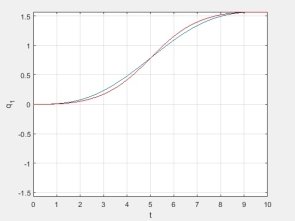
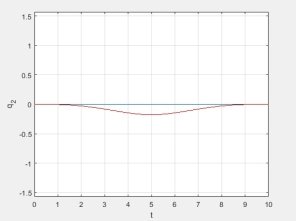
Рис. 5. График изменения

Рис. 6. График изменения

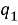
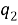
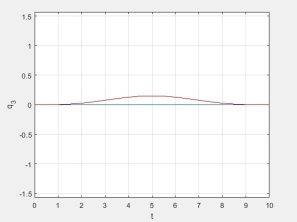
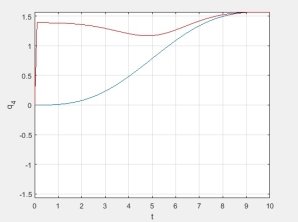
Рис. 7. График изменения Рис. 8. График изменения

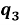
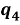
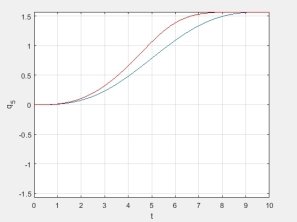
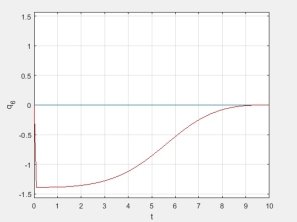
Рис. 9. График изменения Рис. 10. График изменения

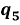
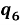
Следует заметить, что в данной задаче для второго типа построения программного движения осуществляется поворот вокруг вектора , причем угол поворота .

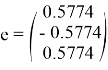
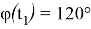
В результате проделанной работы:

1. Аналитически решена обратная задачи о положении и ориентации;
2. Решена задача планирования траектории манипулятора в пространстве обобщенных координат;
3. Сформирована программная траектория в пространстве координат инструмента;
4. Построена программная траектория движения манипулятора на основе программной траектории инструмента;
5. Произведена оценка энергетических затрат манипулятора.

Литература:

1. Зенкевич С. Л., Ющенко А. С. Основы управления манипуляционными роботами: Учебник для вузов. — 2-е изд., исправ. и доп. М.: Изд-во МГТУ им. Н. Э. Баумана, 2004. — 480 с.
2. Шиманчук Д. В. Введение в современную робототехнику. — Санкт-Петербург, 2021. — 233 с.
3. Борисов О. И., Громов В. С., Пыркин А. А. Методы управления робототехническими приложениями. Учебное пособие. — СПб.: Университет ИТМО, 2016. — 108 с.
4. Егоров Е. Е. Моделирование работы манипуляционного робота в программном пакете Matlab Robotics Toolbox. Политехнический молодежный журнал, 2020, № 01(42).