В статье исследованы характеристики свободных колебаний плавающей прямоугольной пластины с учетом эффектов взаимодействия жидкости и конструкции между пластиной и бассейном. Предполагается, что жидкость является невязкой, несжимаемой, а дно бассейна — горизонтальным и жестким. Для решения проблемы их взаимодействия используется метод конечных элементов. Вычисляются собственные частоты пластины и исследуются влияние гибкости пластины и глубины бассейна.
Ключевые слова: гидроупругость, невязкая жидкость, собственная частота, очень большие плавающие конструкции.
В связи с ростом населения и соответствующим спросом на жильё, а также необходимостью в основных и рекреационных объектах на суше, страны с протяженной береговой линией прибегли к мелиорации земель. Но из-за огромных затрат, воздействия на береговые линии, морскую экосистему и иногда конфликты со стороны соседствующих стран, мелиорация не всегда возможна. Так появилась концепция плавучих платформ, и ее не однократно успешно опробовали. Сегодня плавучие платформы используются для различных целей, таких как исследовательские платформы, военно-морские базы, взлетно-посадочные полосы, спасательные базы, парки развлечений и поселения и т. д. Было проведено много исследований. Ранние работы, такие как работа Джона [1], основывались на движении твердых пластин под действием волн. Более поздние исследования были сосредоточены на гибкости больших плавающих пластин. Таким образом, анализ гидроупругости занял центральное место в анализе матообразных плавучих конструкций. Прорывные работы Бишопа и Прайса [2] и Прайса и Ву [3] привели к полной трехмерной теории гидроупругости, в которой метод функции Грина используется для моделирования жидкости. Пластина моделируется как упругая тонкая пластинка со свободными краями. Жидкость несжимаемая, невязкая, и ее движение является безвихревым, так что существует потенциал скорости. Амплитуда падающей волны и движения мега-конструкции малы, потому рассматривается только вертикальное движение конструкции.
Собственные частоты пластины, погруженной или контактирующей с жидкостью, значительно уменьшаются по сравнению с таковыми в вакууме, особенно для основной частоты. Это связано с тем, что вибрация пластины передается жидкости, вызывая увеличение кинетической энергии окружающей жидкости. Хотя точное решение этого типа проблемы взаимодействия трудно получить, существует множество аналитических подходов для пластин различной формы с некоторыми рациональными граничными условиями и приближениями жидкой области. На начальном этапе работы в этой области Лэмб (1920) изучал изменение собственных частот тонкой зажатой круглой пластины в отверстии бесконечно длинной плоской жесткой стенки, контактирующей с водой. Позже Пауэлл и Робертс (1923) [4] экспериментально подтвердили работу Лэмба и Маклахлана (1932) [5], распространив работу Лэмба на круглые пластины без каких-либо опор. Квак и Ким (1991) [6] и позже Квак (1991) [7] получили безразмерные коэффициенты добавленной виртуальной массы (NAVMI) для круглых пластин, размещенных на свободной поверхности жидкости, используя преобразование Ханкеля для осесимметричных мод и всех других мод. Все эти работы основаны на предположении, что формы колебаний пластины остаются неизменными как в контакте с жидкостью, так и в вакууме. Квак (1996) [8] исследовал влияние воды на формы мод и обнаружил, что, кроме основной моды, присутствие воды влияет и на другие. Искажение формы мод увеличивается с увеличением ее номера. Пластина считалась тонкой и изготовленной из изотропного, однородного и линейно упругого материала. Для анализа были приняты теория Кирхгофа для вибрации пластины и аналитический метод Ритца для взаимодействия жидкости и конструкции.
Для решения проблем взаимодействия, хотя аналитические методы обеспечивают лучшую точность, их использование ограничено либо очень частными, либо простыми случаями из-за связанных с этим математических сложностей. Однако из-за наличия высокоскоростных вычислительных средств можно использовать несколько численных методов для получения значимого решения таких сложных проблем. Среди различных используемых численных методов метод конечных элементов (МКЭ) является наиболее предпочтительным из-за его простой реализации в широком круге задач.
Целью настоящей работы является исследование влияния гибкости пластины и глубины жидкости на собственные частоты пластины, плавающей над жидкостью.
- Применение прямоугольной пластины VLFS
В основном есть два типа очень больших плавучих сооружений (VLFS), а именно полупогружные и понтонные. Плавучие конструкции полупогружного типа поднимаются над уровнем моря с помощью колонных труб или балластных конструктивных элементов для минимизации воздействия волн при сохранении постоянной силы плавучести. Таким образом, они могут уменьшить движение, вызываемое волнами, и поэтому их можно использовать в открытом море с большими волнами. Плавучие буровые платформы, используемые для бурения и добычи нефти и газа, являются типичными примерами VLFS полупогружного типа. Когда эти полупогружные аппараты прикреплены к морскому дну с помощью вертикальных тросов с высоким предварительным натяжением, обеспечиваемым дополнительной плавучестью конструкции, их называют платформами с натяжными опорами. Напротив, плавучие конструкции понтонного типа лежат на уровне моря, как гигантская плита, плавающая на воде. Плавучие конструкции понтонного типа подходят для использования только в спокойных водах, часто в бухтах или алагунах и вблизи береговой линии. Большие плавучие конструкции понтонного типа были названы японскими инженерами мегапоплавками. Как правило, мегапоплавки представляют собой плавучие конструкции, длина которых по крайней мере одна из них превышает 60 м. Ссылаясь на рис. 1, система Mega-Float состоит из очень большого понтона плавучей конструкции, причального сооружения, чтобы удерживать конструкцию на месте, подъездного моста или плавучей дороги для доступа к конструкции с берега и волнорез (обычно необходим, если значительная высота волны превышает 4 м) для уменьшения волновых сил, воздействующих на плавучую конструкцию.
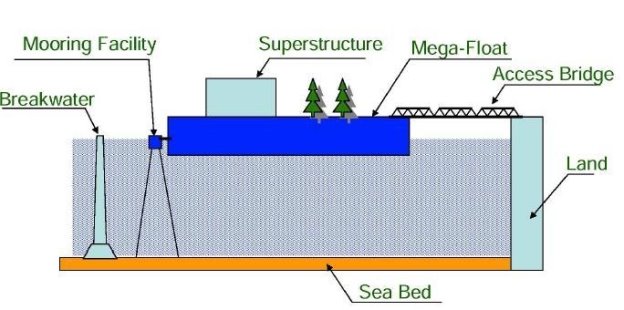
Рис. 1. Элементы плавучей мега-конструкции
- Предмет исследования (прямоугольные VLFS)
Прямоугольная пластина шириной 2a и длиной 2b плавает в резервуаре бесконечной протяженности, как показано на рис. 1. Жидкость считается несжимаемой и невязкой с движением небольшой амплитуды. Влияние статического давления в анализе не учитывается. Предполагается, что дно резервуара горизонтальное и жесткое. Пластина имеет одинаковую толщину, а ее материал однородный, изотропный и линейно-эластичный по своей природе. В ходе анализа трехмерная область жидкости дискретизируется с учетом восьми узловых кирпичных элементов и пластины с использованием четырех узловых четырехугольных пластинчатых элементов. Для данного анализа используется теория изгиба пластины Миндлина.
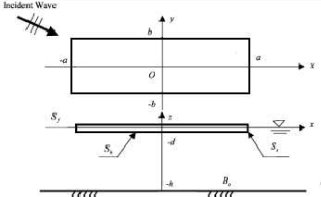
Рис. 2. Понтонный тип VLFS при волновом воздействии
Система координат жидкости и система координат конструкции показаны на рис. 2. Начало системы координат находится на невозмущенной свободной поверхности. Ось z направлена вверх, и морское дно предполагается плоским в точке z = — h. VLFS имеет максимальную длину 2a в направлении x, максимальную ширину 2b в направлении y и уклон d в направлении z. Задача состоит в том, чтобы определить реакцию VLFS на действие волновых сил.
2.1 Основные предпосылки для гидроупругого анализа VLFS
При базовом гидроупругом расчете VLFS понтонного типа обычно делаются следующие допущения:
– VLFS моделируется как упругая (изотропная / ортотропная) тонкая пластина со свободными краями.
– Жидкость несжимаемая, невязкая, и ее движение является безвихревым, так что существует потенциал скорости.
– Амплитуда падающей волны и движения VLFS малы, и учитывается только вертикальное движение конструкции (т. е. мы ограничили горизонтальное перемещение пластины при анализе).
– Между VLFS и свободной поверхностью жидкости нет зазоров.
Анализ может выполняться в частотной области или во временной области. Большинство гидроупругих анализов выполняется в частотной области, что является более простым из двух. Однако для переходных процессов и для нелинейных уравнений движения из-за воздействия системы швартовки или нелинейной волны (как в условиях сильной волны) необходимо выполнять анализ во временной области. Ниже представлены основные уравнения, граничные условия и кратко описаны часто используемые методы анализа в частотной и во временной области.
- Основные уравнения для конструкции пластины
Свободные незатухающие колебания конструкции пластины определяются как
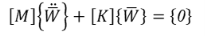
где,
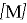
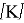
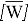
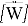
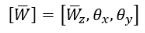
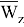
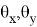
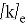
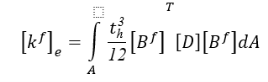
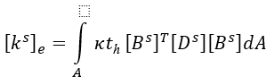
где
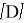
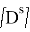
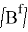
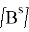
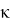
Основное уравнение для области жидкости с учетом невязкой несжимаемой жидкости, имеющей безвихревое движение, имеет вид
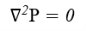
- Граничные условия
Для рассматриваемой задачи с плавающей пластиной приняты следующие граничные условия (рис. 2)
-
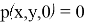
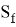
-
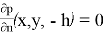
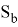
-
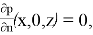
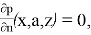
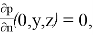
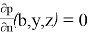
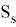
- Анализ во временной области
Обычно используемые подходы для анализа VLFS во временной области — это метод прямого интегрирования по времени [9, 10] и метод, использующий преобразование Фурье [11–15]. В методе прямого интегрирования по времени уравнения движения дискретизируются как для конструкции, так и для жидкой области. В методе преобразования Фурье мы сначала получаем решения в частотной области для жидкой области, а затем преобразовываем результаты Фурье для подстановки в дифференциальные уравнения для упругих движений. Затем уравнения решаются непосредственно при анализе во временной области с использованием метода конечных элементов или других подходящих вычислительных методов.
- Формулировка конечных элементов жидкой области
Взвешенная интегральная форма уравнения 5 над элементом задается как
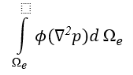
где
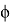
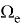
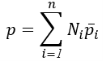
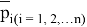
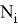
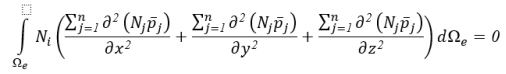
Поскольку значения узлового давления постоянны, исключая их из интегрирования и интегрируя остальные по частям, уравнение 8 можно представить в виде
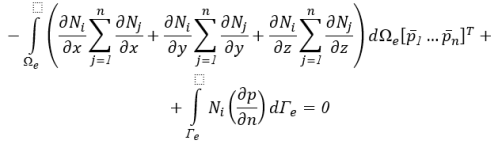
где n — нормаль к поверхности,
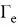
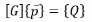
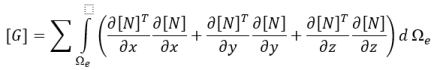
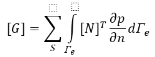
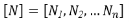
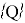
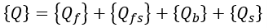
На свободной поверхности
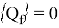
На границе раздела текучей среды
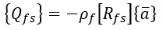
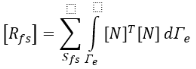
На дне резервуара
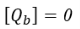
По обе стороны от пластины предполагаемое граничное условие приводит к
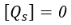
Объединяя все их в
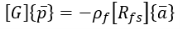
- Совместное перемещение пластины и жидкости
Граничное движение задается движением пластины. Замена ускорения
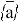
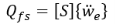
где
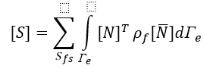
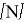
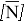

где
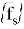
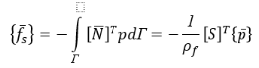
В виде
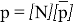
Теперь два связанных уравнения сводятся в
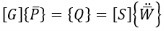
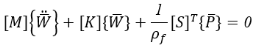
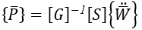
Теперь два связанных уравнения получаются как
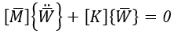
где
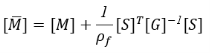
Собственные частоты вычисляются из уравнения 28 используя метод Якоби. Безразмерные частоты представлены как
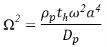
Таблица 1
Собственные частоты пластины 1,0x1,0х0,02 м, плавающей над водой глубиной 1,0 м
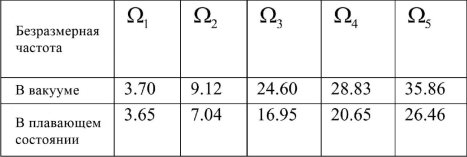
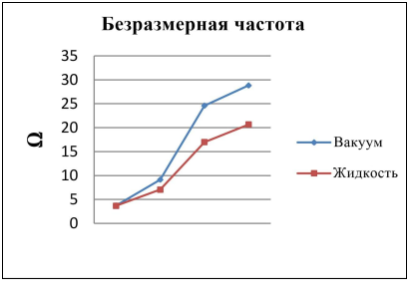
Рис. 3. Безразмерная частота
Таблица 2
Собственные частоты пластины 1,0x1,0 м для разной толщины, плавающей над водой на глубине 1,0 м
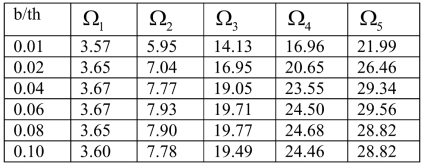
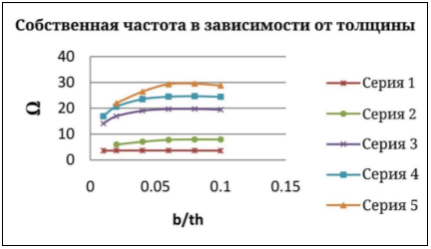
Рис. 4. Собственные частоты для разной толщины
Таблица 3
Собственные частоты пластины 1,0х1,0х0,02 м, плавающей над водой, для разной глубины жидкости
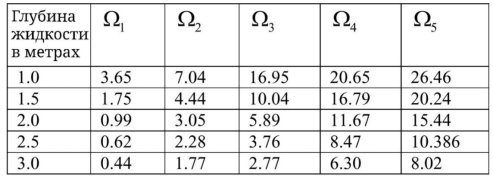
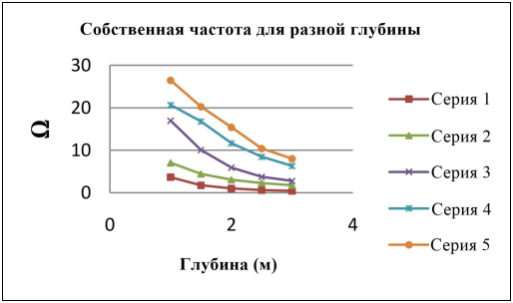
Рис. 5. Собственные частоты для разной глубины
- Результаты, обсуждение и выводы
Изменения собственных частот из-за присутствия жидкости изучаются как для гибкости пластины, так и для глубины жидкости. Как показано на рис. 3, собственные частоты уменьшаются из-за присутствия жидкости. Влияние жесткости пластины на изгиб исследуется путем наблюдения за уменьшением толщины пластины. Как видно из рисунка 4, снижение собственных частот увеличивается с увеличением гибкости пластины. Глубина области жидкости играет важную роль, так как собственные частоты уменьшаются с глубиной жидкости, как показано на рис. 5. Передовые исследования в этой области определенно произведут революцию в отношении острой земельной проблемы и других проблем управления стихийными бедствиями.
Литература:
- Джон Ф. О движении плавающих тел. Сообщения по фундаментальной и прикладной математике, часть 1, т. 2, стр. 13–18, 1949.
- Бишоп Р. Введение в гидроупругость корабля, Журнал звука и вибрации, т 87, вып. 3, стр. 391–407, 1983.
- Прайс В. Г., Ву Ю. В: Ниордсон Ф. И., Ольхофф Н. Гидроупругость морских структур, теоретическая и прикладная механика. Издательство Elsevier Science, стр. 311–371, 1985.
- Пауэлл, Дж. Х. и Робертс, Дж. Х. Т. О частоте колебаний круговых диафрагм, Труды Физического Общества, Лондон, т. 35, стр. 170–182, 1923.
- Маклахлан Н. В. Присоединение к инерции гибких дисков, вибрирующих в жидкости, Труды Физического Общества, Лондон, вып. 44, стр. 546–555, 1932.
- Квак, М. К. и Ким, К. С. Осесимметричные колебания круглых пластин в контакте с жидкостью, Журнал звука и вибрации, т. 146 (3), стр. 381–389, 1991.
- Квак, М. К. Вибрация круглых пластин при контакте с водой, Журнал прикладной механики, ASME, т. 58, стр. 480–483, 1991.
- Квак, М. К. Гидроупругие колебания прямоугольных пластин, Журнал прикладной механики, ASME, т. 63, стр. 110–115, 1996.
- Ватанабэ Э., Уцуномия Т. Анализ переходного отклика VLFS при посадке самолета. Международный семинар по очень большим плавучим конструкциям, Хаяма, Канагава, Япония, стр. 24–27, 1996.
- Ватанабэ Э., Уцуномия Т., Танигаки С. Анализ переходных характеристик очень большой плавучей конструкции методом конечных элементов, Журнал Структурная инженерия / сейсмостойкость, JSCE, т. 15(2), стр. 155–163, 1998.
- Ohmatsu S. Numerical calculation of hydroelastic behaviour of VLFS in time domain. Proc 2nd Int Conf.Hydroelastic MarineTech, Fukuoka. 1998, p. 89–97.
- Endo H, Yago K, Chiaki S. Elastic responses of a floating platform stimulated by dynamic load. Proc 14th OceanEng Symp, SocNav Arch Japan. 1998, p. 411–6.
- Endo H. The behaviour of a VLFS and an airplane during takeoff/landing run in wave condition. Marine Structures 2000;13: 477–91.
- Kashiwagi M. A time-domain mode-expansion method for calculating transient elastic responses of a pontoon- type LFS.Marine SciTechnol 2000; 5: 89–100.
- Miao Q, Du S, Dong S, Wu Y. Hydrodynamic analysis ofa moored very large floating structure. In: Watanabe Y, editor.Proc Int Workshop on Very Large Floating Structures, Hayama,Kanagawa, Japan, November 25–28.1996, p. 201–8.







