В статье приводится краткое описание процесса проектирования и разработки программы алгоритма метода Рунге-Кутта четвертого порядка для решения систем дифференциальных уравнений на примере системы Лоренца.
Ключевые слова: Рунге-Кутта четвертого порядка, система Лоренца, решение дифференциальных уравнений, С++, Python.
Численный метод Рунге-Кутта часто используется для решения задач научного и инженерно-технического характера. Метод эффективен, надежен и реализуется программными средствами. Существует несколько разновидностей метода Рунге-Кутта, различающиеся порядком точности. В данной работе рассматривается явный метод Рунге-Кутта 4-го порядка точности для решения задачи Коши.
Решение систем дифференциальных уравнений методом Рунге — Кутта 4 порядка
В данном методе вводятся вспомогательные величины k0, k1, k2, k3. Вычисление координат очередной точки (x i +1 , y i +1 ) происходит исходя из уже известных координат предыдущей точки.
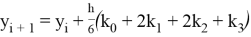
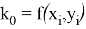
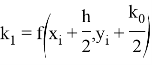
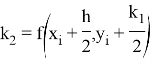
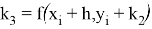
Таким образом, метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения f(x, y).
Данный метод требует большого объема вычислений, однако это окупается повышенной точностью, что дает возможность проводить счет с большим шагом.
Рассмотренный метод может быть использован также для решения систем дифференциальных уравнений.
Система Лоренца
Наиболее яркий пример динамического хаоса обнаружил в 1963 году метеоролог Эдвард Лоренц, решая задачу о тепловой конвекции жидкости.
Максимально упрощая уравнения, описывающие это явление, Лоренц вывел, что даже сравнительно простая система из трех связанных нелинейных дифференциальных уравнений 1-го порядка может иметь решением совершенно хаотические траектории.
Эта система уравнений, ставшая теперь классической, имеет вид:
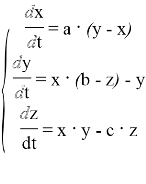
Решение этих уравнений — функции X(t), Y(t) и Z(t) — определяют в паpаметpическом виде тpаектоpию системы в тpехмеpном «фазовом» пpостpанстве X, Y, Z. Ввиду однозначности функций, стоящих в правых частях этих уравнений, тpаектоpия себя никогда не пересекает.
Лоpенц исследовал вид этих тpаектоpий пpи разных начальных условиях пpи значениях паpаметpов a = 10, b = 28 и c = 8/3. Он обнаружил, что пpи этом тpаектоpия хаотическим образом блуждает из полупpостpанства x>0 в полупpостpанство x<0, фоpмиpуя две почти плоских, пеpепутанных сложным образом спирали.
Проектирование
Основная программа реализована на языке С++.
Так как в решаемой системе Лоренца четыре неизвестных: t, x, y, z, рассчитывать вспомогательные величины k0, k1, k2, k3 надо будет для x, y, z. Будем считать наши уравнения относительно t. Для этого в массиве t будем хранить значения: предыдущее значение плюс шаг начиная с 0.
Для хранения всех k воспользуемся двумерным массивом 3 на 4.
Также для хранения координат новых точек тоже воспользуемся двумерным массивом.
Для записи массивов с полученными точками в файлы используем библиотеку «fstream».
Входные данные программы это:
– Коэффициенты a, b, c;
– Шаг h;
– Количество точек, которые надо вычислить;
– Начальные значения x, y, z.
Выходные данные — это массивы точек x, y, z записанные в файлы формата.txt. Схема основной программы на рисунке 1.
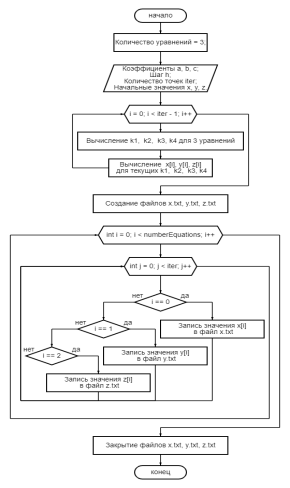
Рис. 1
Вспомогательная программа для вывода графиков на экран написана на языке Python.
Для построения графиков понадобится библиотека «matplotlib.pyplot».
Входные данные программы — массивы точек x, y, z считанные из прежде сохраненных файлов.
Выходные данные — 3D график, построенный из массивов точек x, y, z. Схема вспомогательной программы на рисунке 2.
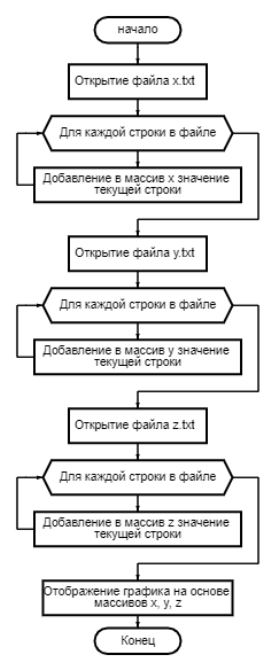
Рис. 2
Результаты работы программы
Запустим программу. возьмем шаг = 0.01, коэффициент a = 10, коэффициент b = 28 (считается классическим случаем), коэффициент c = 2.6, начальные координаты (10,10,10), количество точек = 3000. Получившийся график показан на рисунке 3.
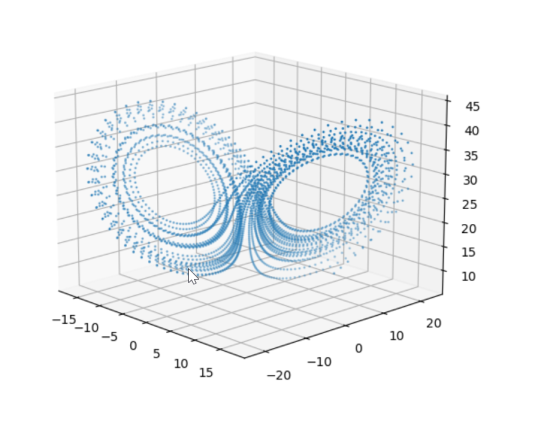
Рис. 3
Выводы
По результатам разработки можно убедиться, что метод Рунге-Кутты четвертого порядка достаточно просто реализуем, а также точен. Его удобно и эффективно использовать для решения задач научного и инженерно-технического характера.
Литература:
- Демченко В. В. Метод Рунге-Кутты решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка. М.: МФТИ, 2004. -20с.
- Арнольд В. И. Обыкновенные дифференциальные уравнения. — М.: МЦНМО, 2012. — 344 с.
- Лоренц Э. Детерминированное непериодическое движение. Странные аттракторы. — М.:, 1981. — С. 88–116.
- Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. — Наука, 1969. — 425 c.







