В статье приводится краткое описание процесса проектирования и разработки алгоритма, выдающего псевдослучайные числа.
Ключевые слова: псевдослучайные числа,алгоритм Лемера, алгоритм Вичмана-Хилла, линейный конгруэнтный метод, С++.
Введение
Генератор псевдослучайных чисел (ГПСЧ) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению.
ГПСЧ — одна из ключевых частей веб-безопасности. Она часто используется в криптографии, однако не все методы имеют хорошую криптозащищенность.
Методы генерации псевдослучайных чисел
Алгоритм для генерации псевдослучайных чисел существует большое множество. Рассмотрим некоторые из них:
1.1. Метод Фибоначчи с запаздываниями
Этот метод можно описать следующей формулой:
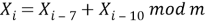
В данном алгоритме каждое последующее число является тем, которое было сгенерировано 7 шагов назад, плюс случайное число, которое было сгенерировано 10 шагов назад и деленное по модулю на большее значение
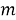
1.2. Метод серединных квадратов
Данный метод был предложен Нейманом, суть данного метода заключается в том, что выбирается число меньше 1 разрядностью 2n и возводится в квадрат. Из полученного результата, разрядность которого должна быть 2*2n (если нет, то добавляются два нуля справа от полученного числа) выбираются 2 n чисел из середины полученного после возведения в квадрат числа. Число записывается после десятичной точки. Далее процедура повторяется.
1.3. Алгоритм Лемера.
Данный алгоритм был предложен Д.Лемером в 1988 году и в качестве входных значений берет a = 16807 и m = 2147483647, позднее в 1993 году Лемер использовал a = 48271 как более качественную альтернативу. Однако, алгоритм Лемера как и алгоритм Вичмана-Хилла является лишь частным случаем линейного конгруэнтного метода и рассчитывается по следующей формуле:
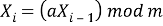
где m — модуль(m≥2), а — множитель (0≤a≤m)
1.4. Метод Вичмана-Хилла.
Этот алгоритм датируется 1982 годом. Идея Вичмана-Хилла заключается в генерации трех предварительных результатов и последующим их объединением в один финальный результат.
Так как данный алгоритм использует три разных генерирующих уравнения, ему требуется трое начальных значений, в данном случае это 30269, 30307, 30323 Алгоритм Вичмана-Хилла немногим сложнее, чем алгоритм Лемера, но его преимущество заключается в том, что он генерирует более длинную последовательность псевдослучайных чисел, прежде чем начнет повторяться.
1.5. Линейный Конгруэнтный Метод
Данный алгоритм — это один из методов генерации псевдослучайных чисел. Линейный конгруэнтный метод был предложен Д.Лемером в 1949 году. Суть данного метода заключается в вычислении последовательности случайных чисел по формуле:
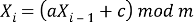
где m — модуль(m≥2), а — множитель(0≤a≤m), с — приращение (0≤
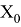
Эта последовательность называется линейной конгруэнтной последовательностью. Главным недостатком данного алгоритма является то, что он не криптографически стойкий.
Проектирование
Для реализации ГПСЧ был выбран язык C++, в качестве компилятора был выбран G++, так же для реализации математической части ГСПЧ использовались: алгоритм Вичмана-Хилла, алгоритм Лемера, которые в свою очередь основываются на линейном конгруэнтном алгоритме.
Для реализации методов ГПСЧ создадим три класса:
— Lemer — класс, в котором реализован метод Лемера;
— Witchman — класс, в котором реализован метод Вичмана-Хилла;
— MyClass — класс, в котором реализован мой метод, основанный на линейном конгруэнтном методе.
Алгоритм, написанный в классе MyClass, так же является частным случаем линейного конгруэнтного метода. В качестве входных значений используются константы b1, b2, b3. Получаемый результат генерируется путем генерации случайного seed’а алгоритмом Лемера и последующей генерации трех случайных чисел линейным конгруэнтным методом, результат же получается по следующей формуле:
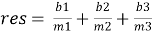
m1, m2 и m3 — произвольные целые числа типа int.
Для хранения данных полученных при генерации чисел воспользуемся массивом. Алгоритм работы программы представлен на рисунке 1.
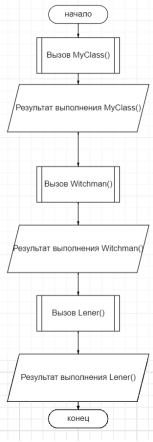
Рис. 1
Результаты работы программы
В качестве выходных данных использованы те же массивы и переменные, что и во входных данных, только полностью обновленные, содержащие необходимые данные для вывода.
В результате запуска программы на монитор выводится окно, представленное на рисунке 2.
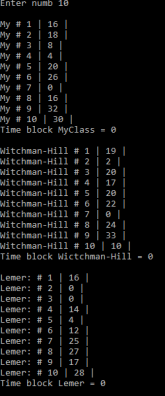
Рис. 2
Выводы
В результате был разработан генератор псевдослучайных чисел, основанный на алгоритме Вичмана-Хилла и алгоритме Лемера, которые в свою очередь основываются на линейном конгруэнтном алгоритме.
Литература:
- Такач, Л. Комбинаторные методы в теории случайных процессов/ Л. Такач. — М.: 1999. — 266 c.
- Столов, Евгений Генераторы случайных чисел. Математическая теория / Евгений Столов. — М.: LAP Lambert Academic Publishing, 2014. — 443 c.
- Манин, Ю. И. Введение в теорию чисел / Ю. И. Манин, А. А. Панчишкин. — М: 1990. — 672 c.
- Шор, Е. В мире случайностей / Е. Шор. — М.: [не указано], 1977. — 804 c.







