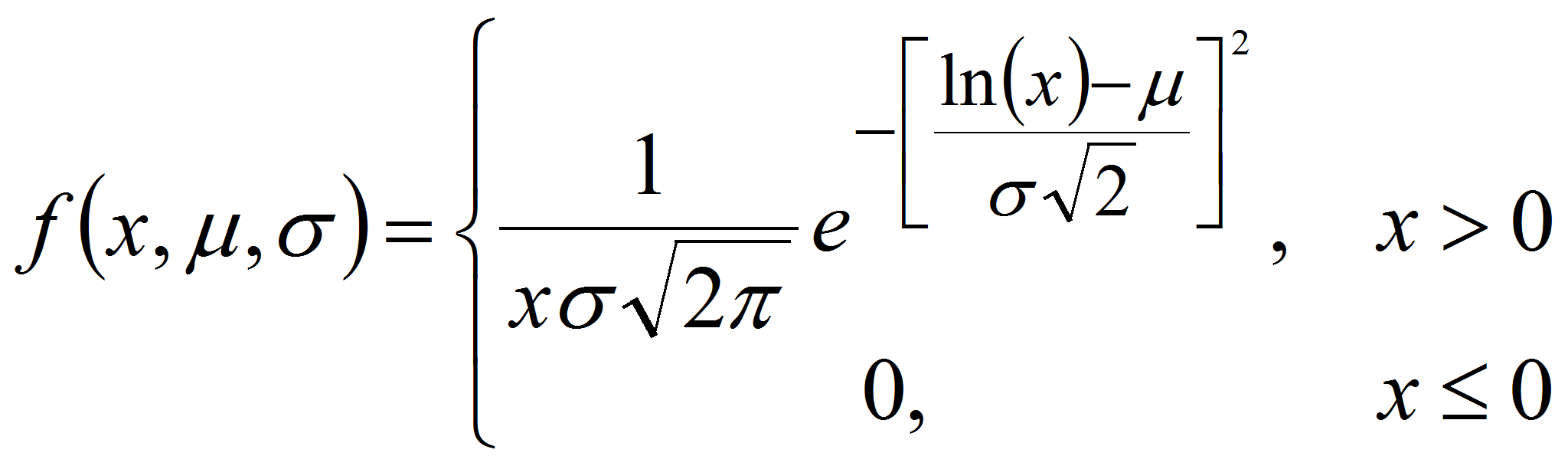Прецизионный генератор псевдослучайных чисел

Рассматривается задача формирования выборок реализаций случайных величин с высокой степенью согласованности с законом распределения этих случайных величин. Производится исследование полученных выборок реализаций случайных величин распределенных по логнормальному закону. Предлагается несколько способов формирования выборок для случайных величин с быстро изменяющейся плотностью распределения вероятностей и большой дисперсией.

Теория вероятностей, а позднее и математическая статистика как разделы науки появились ещё в средние века и использовались для изучения азартных игр. Отличительной особенностью данных направлений является представление окружающего мира в виде череды событий характеризующихся свойством, названным «вероятность». Вероятность события – это мера возможности наступления этого события. Вероятность – это искусственно присвоенная каждому событию численная характеристика, которую используют для однозначного описания того, возможно ли наступление того или иного события и как много времени может пройти до его наступления.

Современная теория вероятностей и математическая статистика, основанная на аксиоматике Андрея Николаевича Колмогорова [1], позволяет, пользуясь математическим аппаратом, описать стохастические особенности окружающего мира, учитывать эти особенности при проектировании прикладных систем. Однако иногда в ходе проектирования возникают специфические потребности к качеству описания стохастических свойств окружающих среды, вопросу изучения одной из таких специфических потребностей посвящена данная статья.

Прежде чем перейти к задаче, которой посвящена статья, необходимо привести ещё один термин, используемый в работе. В терминах теории вероятностей и математической статистики встречается понятие «случайная величина» - это абстрактное понятие, необходимое для описания случайных (непредсказуемых) проявлений природы и среды. В труде [1], автор раскрывает понятие данного термина в главах III и IV. В данной работе термин используется для обозначения случайных явлений, обладающих свойствами, которые описываются законом и плотностью распределения случайных величин.

Постановка задачи

Настоящая статья посвящена задаче формирования множества чисел, каждое из которых является реализацией некоторой случайной величины (С.В.), другими словами является подмножеством множества всех значений данной С.В. Помимо этого, на множество полученных чисел накладывается условие высокой степени их согласованности с законом распределения С.В.

Математическая постановка задачи звучит так: необходимо сформировать множество (далее выборка значений С.В.) размером , каждый элемент которого является элементом множества всех возможных значений случайной величины распределенной по закону распределения , с плотностью распределения , доставляющее критерию согласованности выборки значений С.В. и закона распределения С.В. максимальное значение . Данное определение может быть видоизменено в силу того, что функции закона и плотности распределения случайных величин однозначно связаны дифференциальным оператором.

Критерием согласованности будем называть функционал, характеризующий степень согласия выборки значений С.В. и её закона распределения. В ходе анализа критериев согласованности было отмечено две группы критериев, отличающиеся самим принципом определения степени согласия:

1. Параметрические критерии. Принцип работы таких критериев следующий: исследователь, по некоторому правилу (например, используя метод максимального правдоподобия, метод моментов и т.д.) определяет оценки параметров закона распределения. Полученные оценки сравниваются со значениями истинных параметров закона распределения С.В. Разница между оценками параметров и значениями параметров характеризует степень согласованности выборки значений С.В. и закона распределения С.В;

2. Непараметрические критерии. В группу этих критериев входят критерии, рассчитывающие степень согласия при помощи сравнения закона распределения С.В. с эмпирическим законом распределения С.В. К таким критериям относятся: критерии Колмогорова-Смирнова, Пирсона, Андерсона-Дарлинга, а также ряд критериев, специализированных для нормального распределения: Z-тест, критерии Жака-Бера, Шапиро-Уилко.

Алгоритм работы прецизионного генератора

Принцип, на котором основываются непараметрические критерии согласия, а именно принцип согласованности закона распределения С.В. и эмпирического закона распределения С.В. послужил основанием для создания прецизионного генератора псевдослучайных чисел, о котором ведется речь в статье. Принцип работы прецизионного генератора заключается в генерации независимых друг от друга чисел, являющихся реализациями случайной величины, закон распределения которой является оценкой желаемого закона распределения. В данной работе описан алгоритм прецизионного генератора псевдослучайных чисел использующих в качестве оценки закона распределения гистограмму.

Алгоритм работы прецизионного генератора псевдослучайных чисел (П-генератора) состоит из четырёх этапов:

1. Формирование задания. Определяется требуемый объем выборки 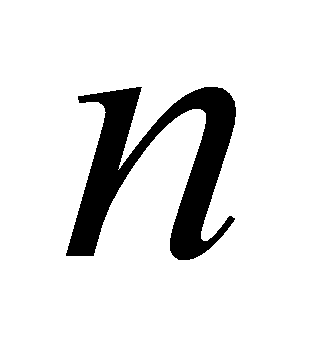, закон распределения С.В. 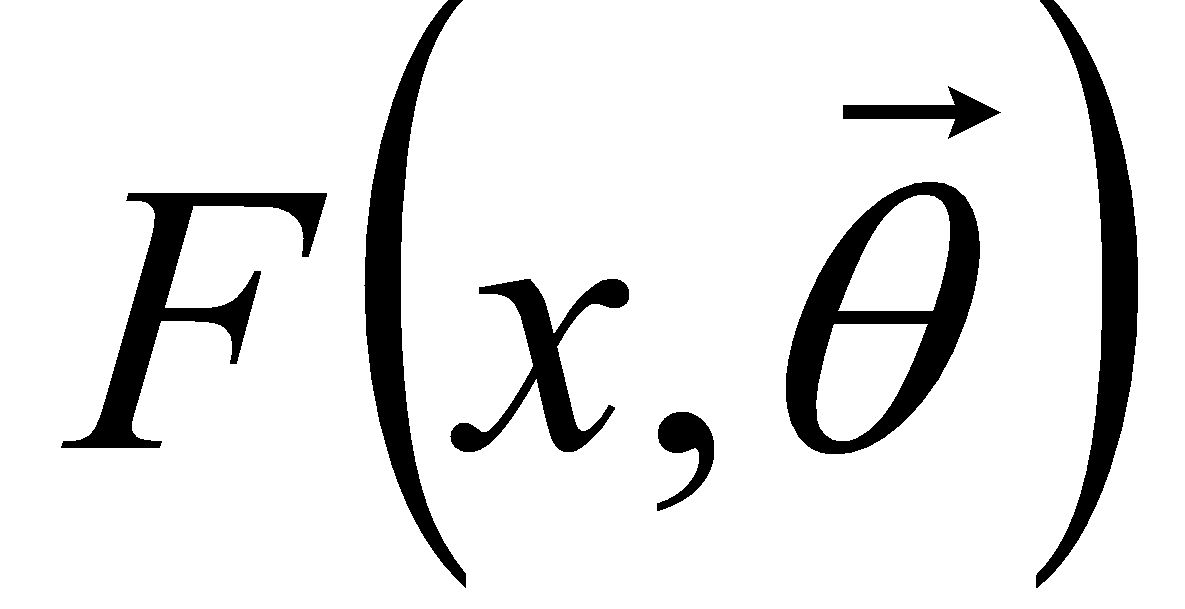, с точностью до параметров, а также значения самих параметров ;

2. Ограничение закона распределения. Происходит определение границ области значений 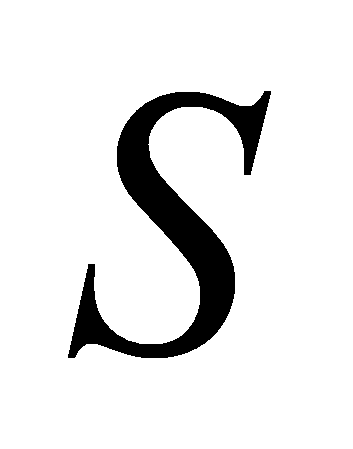случайной величины 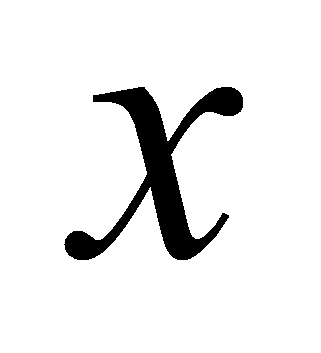. Это параметр, необходимый для построения оценки закона распределения С.В. Все реализации С.В. полученные в результате работы П-генератора попадут в область значений 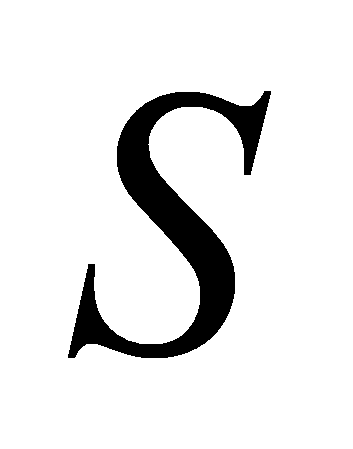, и ни одна из них не выйдет за её пределы;

3. Оценка закона распределения. Область значений 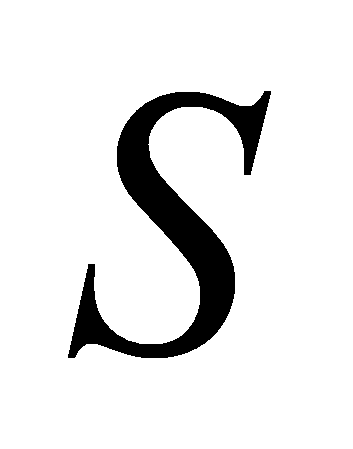С.В. равномерно разбивается на 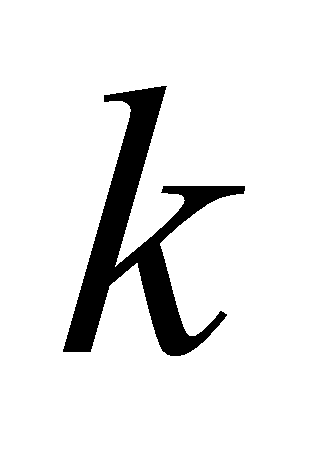равных по площади подынтервала. Для каждого подынтервала, по определенному правилу, рассчитывается значение функции плотности распределения вероятностей 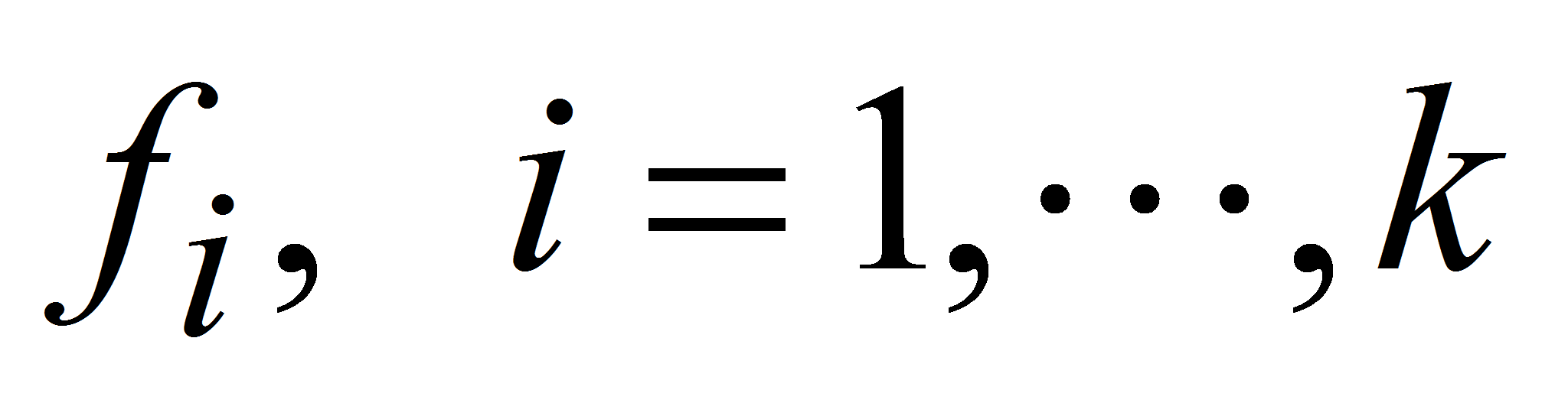(например, берётся значение функции плотности в центре подынтервала);

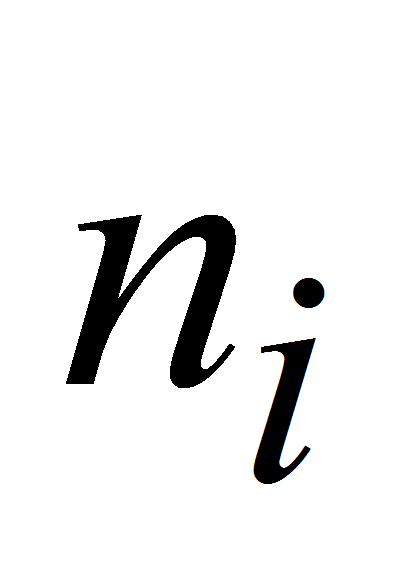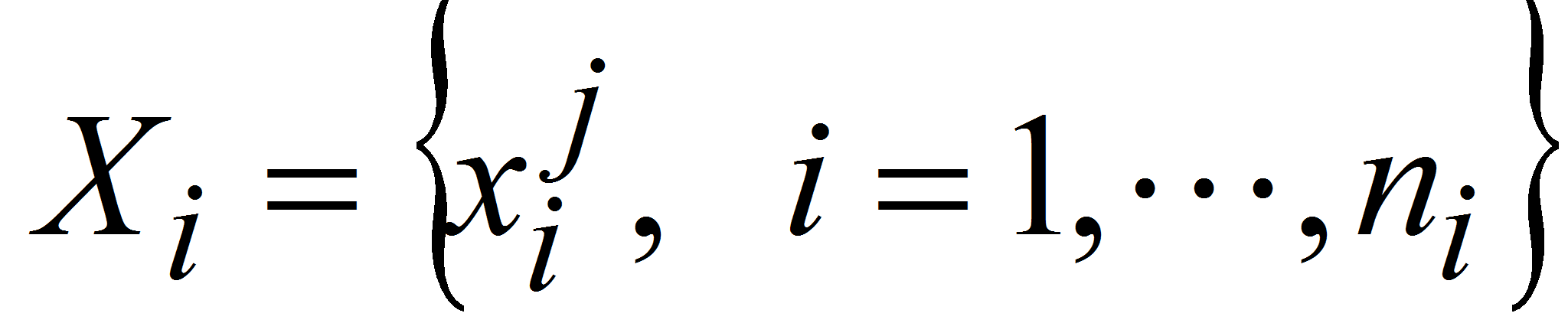4. Генерация выборки. В каждый подынтервал случайным образом генерируется точек , распределенных по равномерному закону распределения. Количество точек 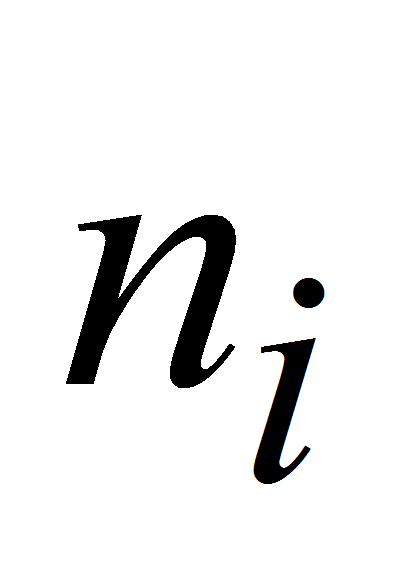в каждом подынтервале пропорционально значению , а их сумма равняется требуемому объему выборки 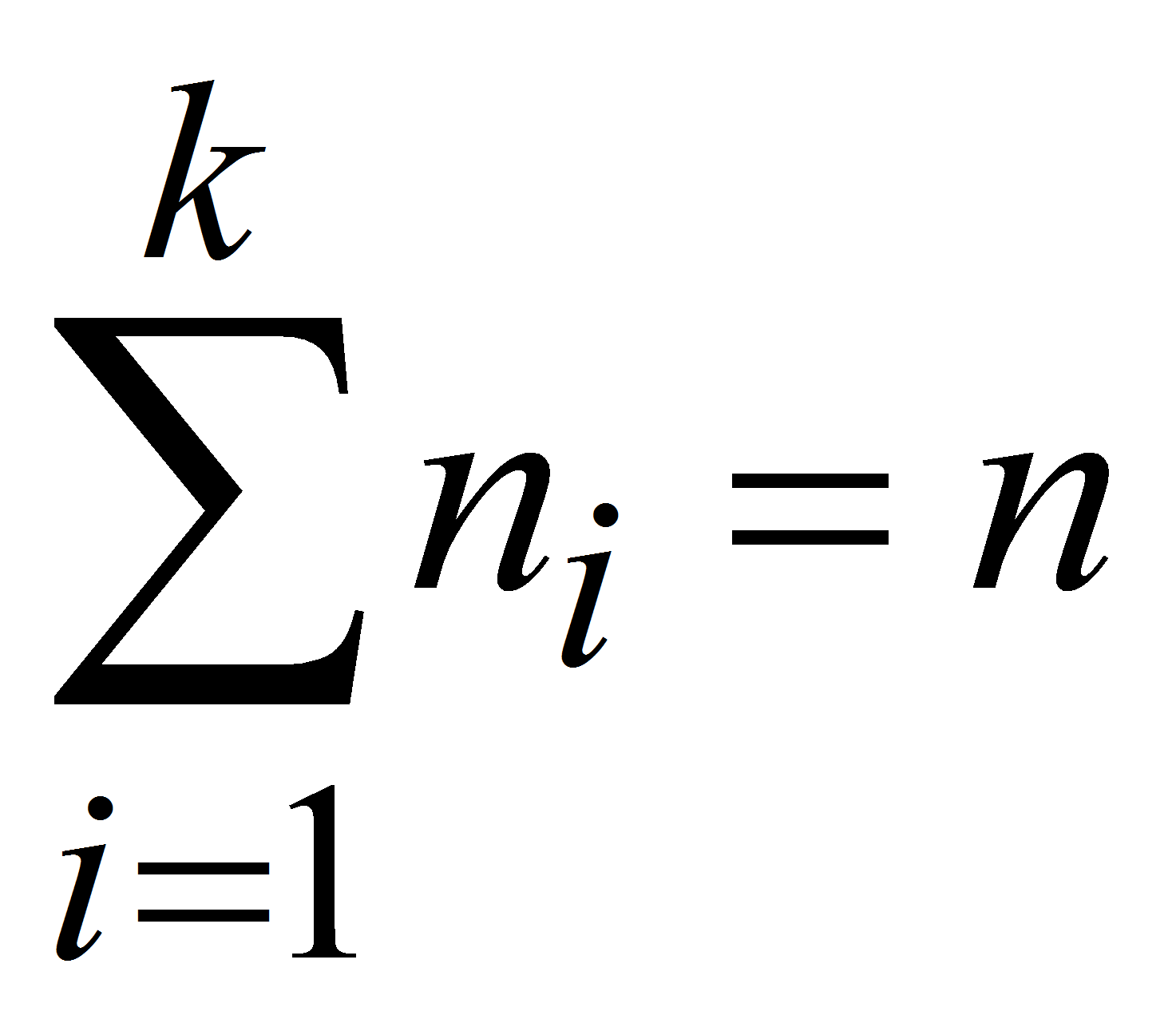. Совокупность всех полученных точек и является множеством реализаций С.В., закон распределения которой близок к .

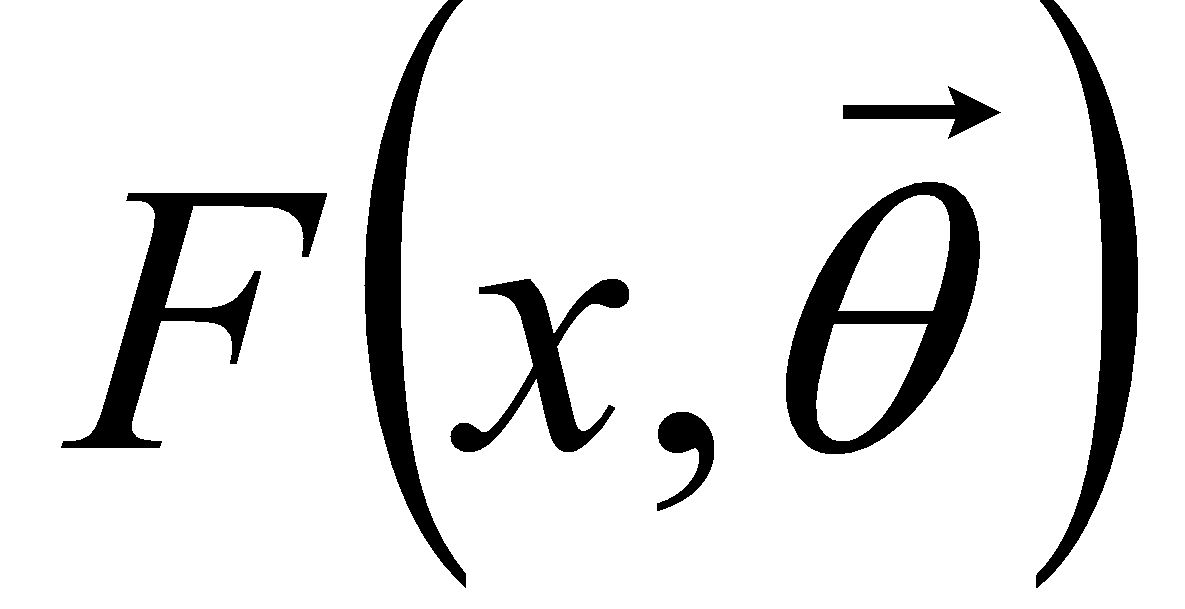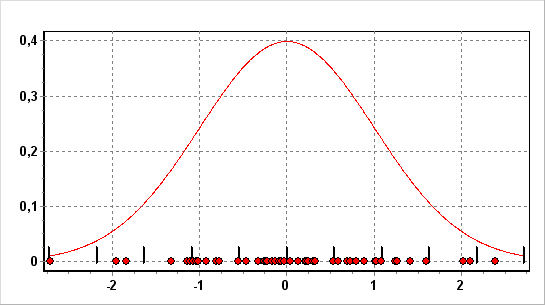
Принцип и результаты работы П-генератора изображены на рис.1.

Рис.1. Работа П-генератора

На рис.1 изображены результаты работы П-генератора. В данном примере рассматривается задача генерации выборки значений случайной величины распределенной по стандартному нормальному закону. Кривая на Рис.1 изображает плотность распределения стандартного нормального закона, ограниченная интервалом (множество значений ), на концах которого плотность незначительно отличается от нуля. Область разбита на 10 равных по длине подынтервала, в каждый из которых генерировалось определенное количество точек, так чтобы их количество было пропорционально значению функции плотности в середине подынтервала. На Рис.1 границы подынтервалов изображены в виде вертикальных линий внизу графика. Точками на графике изображены 50 точек выборки, полученной в результате работы П-генератора. Построив гистограмму по данной выборке с данным количеством подынтервалов, можно убедиться в высокой согласованности стандартного нормального закона и этой гистограммы.

Исследования прецизионного генератора

Качество работы П-генератора оценивается при помощи критериев согласованности. Значение критерия показывает степень согласованности выборки значений С.В. с законом распределения этой С.В. Использование критериев необходимо для того, чтобы определить оптимальное значение параметров генератора, для того чтобы получить выборку с максимальной степенью согласованности с законом распределения.

Вопросу получения выборки с максимальной степенью согласованности с законом распределения посвящена оставшаяся часть работы. Ниже приведены выводы, основанные на результатах проведения исследований качества работы П-генератора, в смысле степени согласованности выборки и закона распределения, в зависимости от различных параметров алгоритма. Также, описаны специфические проблемы, возникшие в ходе исследования качества работы П-генератора при генерации выборки С.В., распределенных по логнормальному закону распределения. Приведены идеи и алгоритм реализующий подход позволяющий решить эти специфические проблемы.

Объектом исследований стало качество выборок, полученных в результате генерации П-генератором выборки значений случайных величин, распределенных по логнормальному закону распределения. «Логнормальное распределение используется для исследования большого числа разнообразных процессов, используется для описания экономических, геофизических и многих других явлений. В общем случае, логнормальный закон достаточно хорошо описывает случайные величины, являющиеся произведением большого числа независимых или слабо зависимых неотрицательных случайных величин» [2]. Функция плотности логнормального распределения описывается функцией (1):

где - значение С.В., - параметр сдвига, - параметр масштаба.

Для оценки степени согласованности выборки с законом распределения было принято решение использовать многократное повторение опытов с использованием критериев из группы параметрических, а именно значение квадрата разницы средневыборочных оценок обоих параметров закона распределения и самих параметров закона распределения, а также среднеквадратическое отклонение этих оценок. Первый критерий показывает степень согласованности выборки и закона распределения в среднем по всем опытам, второй критерий позволяет оценить насколько сильно отклонение степени согласованности, тем самым позволяя видеть статистическую устойчивость П-генератора. Для статистического подтверждения результатов исследований было принято решение о проведении большого количества опытов.

Таким образом, в результате проведенных исследований, часть результатов которых было опубликовано в работах [2, 3], были сделаны следующие выводы:

Общих рекомендаций по выбору границ области значений выборки случайной величины нет. Выбранные для изучения критерии имеют немонотонный характер поведения при варьировании границ области значений. Используя П-генератор, следует выбирать границы области значений исходя из практических рекомендаций, опыта и руководствоваться здравым смыслом.

Значение параметра алгоритма П-генератора «количество подынтервалов» следует выбирать достаточно большим, для того, чтобы выборка значений С.В. была «чувствительна» к изменениям функции плотности С.В. Однако выбор слишком большого числа подынтервалов, особенно при небольших объемах выборки, может привести к получению несогласованной выборки с законом распределения С.В. Количество подынтервалов следует выбирать в пределах , где - объем выборки.

Исследования логнормального распределения обнаружили одну специфическую особенность распределения, оказывающую значительное влияние на качество работы П-генератора. Особенность заключается в том, что логнормальное распределение описывает случайные величины, имеющие области в которых наблюдается большое скопление значений, а также имеющие большое разброс значений, другими словами функция плотности логнормального распределения значительно изменяется вначале оси значений С.В. и продолжает незначительно убывать в направление увеличения значений С.В. Практические результаты показывают, что использование П-генератора для генерации выборок значений С.В. распределенных по логнормальному закону не всегда приводит к удовлетворительным результатам.

Для решения проблемы неудовлетворительного качества выборок С.В. распределенных по логнормальному закону, полученных при помощи П-генератора, было предложено два способа:

Первый способ заключается в том, чтобы использовать П-генератор с заведомо большим количеством подынтервалом и завышенным количеством точек в выборке. После формирования выборки предлагается случайным образом исключать точки из выборки до тех пор, пока её объем не станет равным требуемому. Таким образом, за счет повышения количества подынтервалов предполагается «повысить чувствительность» алгоритма к быстрому изменению функции плотности. Увеличение объема выборки позволяет учитывать большую дисперсию С.В. В работе [2] приводятся результаты исследований качества выборок, полученных путем случайного исключения точек из выборки. На основании данных исследований можно сделать вывод о том, что исключение точек из выборки может влиять на качество выборки, в смысле её согласованности с законом распределения, и чем больше точек исключается, тем больше может наблюдаться разница между законом распределения от эмпирической функцией распределения.

Второй способ предполагает использование неравномерной сетки границ подынтервалов в алгоритме П-генератора. Идея данного подхода заключается в изменении принципа работы П-генератора, различия работы двух алгоритмов можно описать так: при работе с П-генератором пользователь определяет количество подынтервалов, с фиксированной длиной, алгоритм рассчитывает количество точек, попадающих в каждый из подынтервалов; алгоритм с неравномерной сеткой границ подынтервалов предполагает фиксацию количества точек, попадающих в каждый из подынтервалов, при этом длина подынтервала вычисляется алгоритмически. Ниже приведен алгоритм, реализующий такой подход, в котором количество подынтервалов равно объему выборки, то есть в каждый из подынтервалов генерируется только одна точка.

Алгоритм генератора с неравномерной сеткой границ подынтервалов:

1. Формирование задания. Определяется требуемый объем выборки 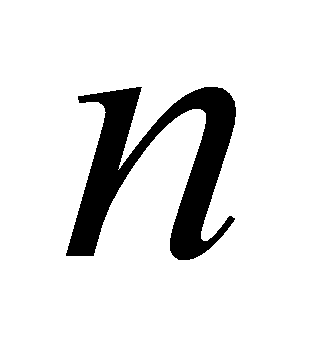, закон распределения С.В. 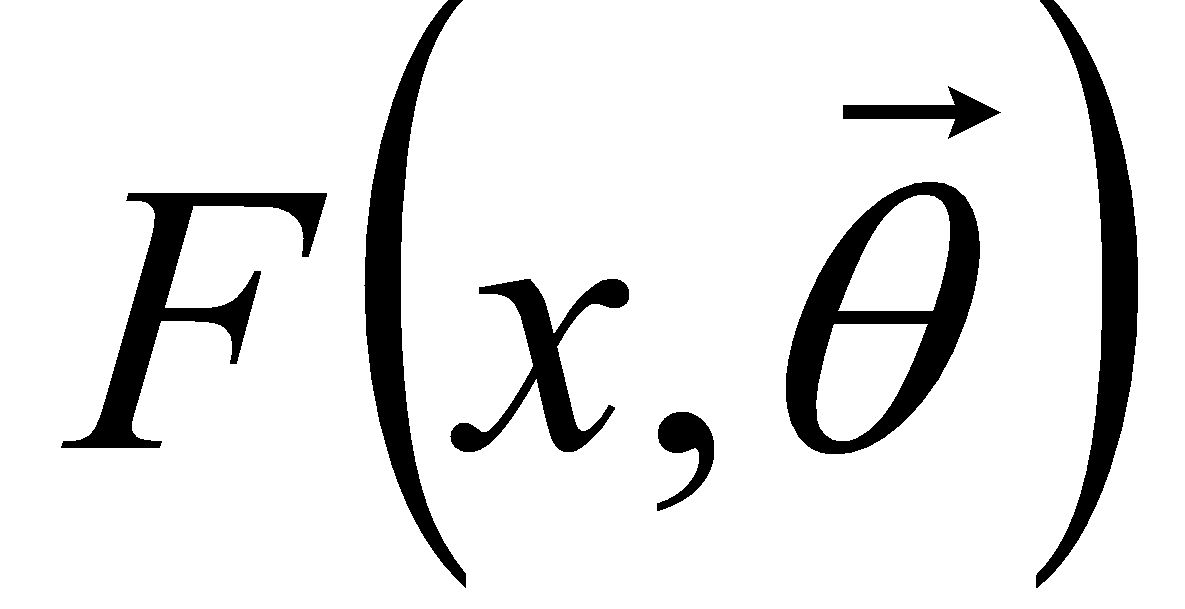, с точностью до параметров, а также значения самих параметров ;

2. Ограничение закона распределения. Происходит определение границ области значений 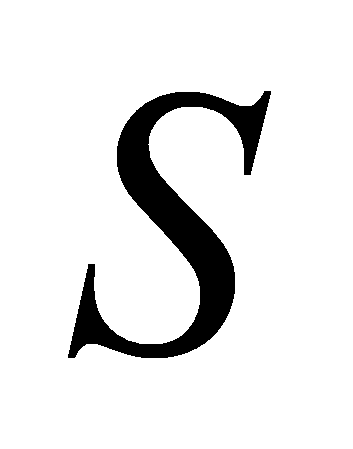случайной величины (область значений 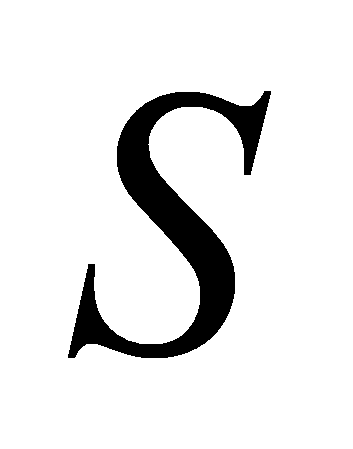представляет собой интервал 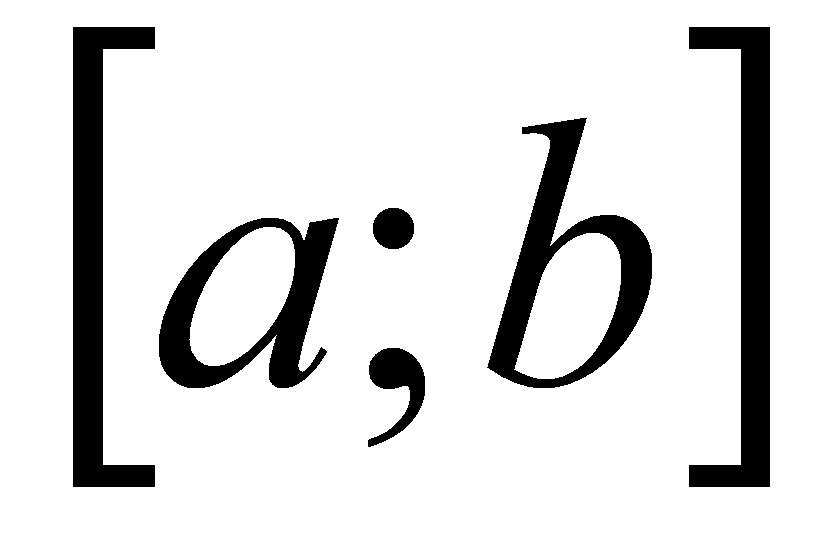). Область значений делится на 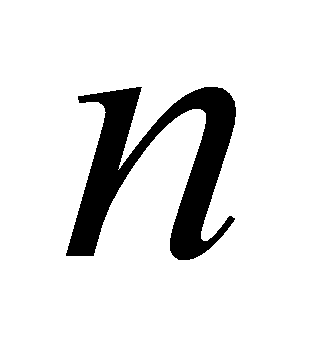равных подынтервалов, границы подынтервалов обозначаются 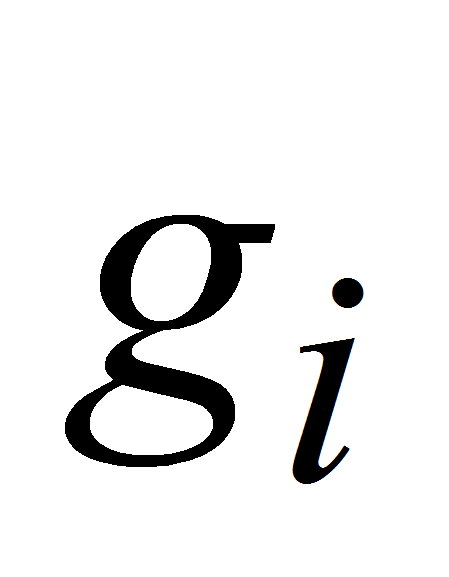и 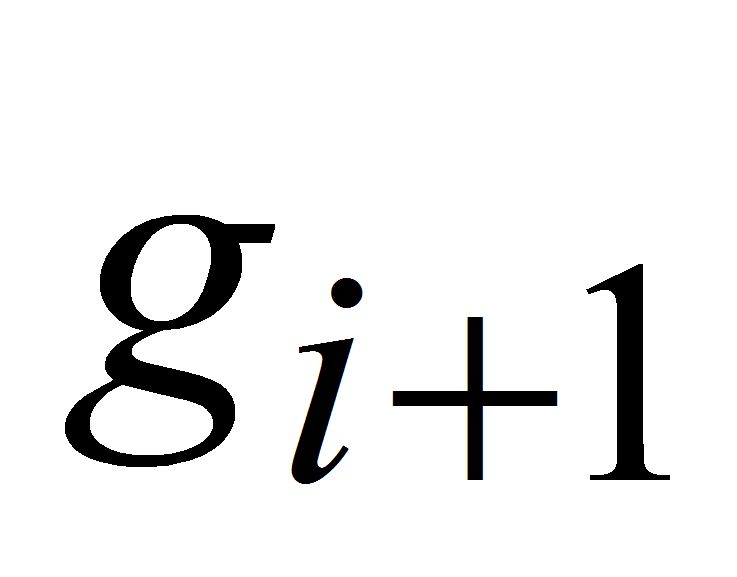для интервалов под номер 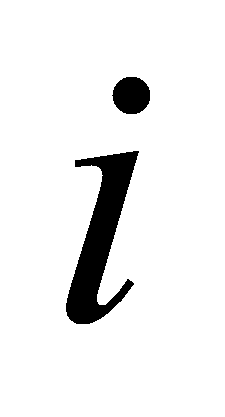. Номер итерации ;

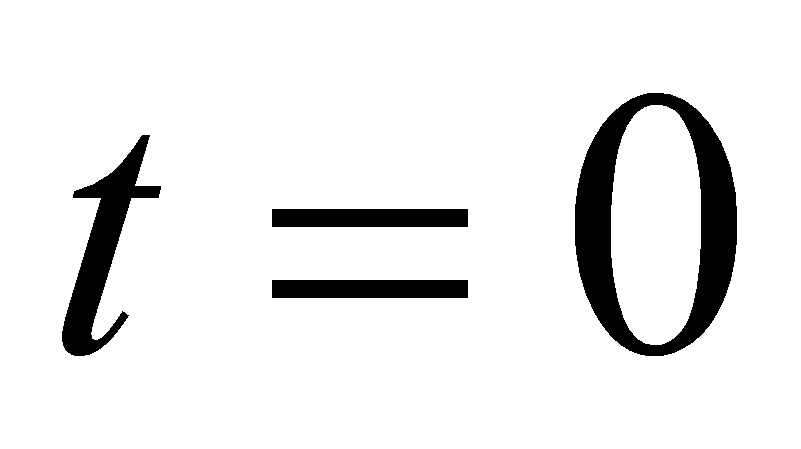3. Пересчет границ. Увеличивается номер ит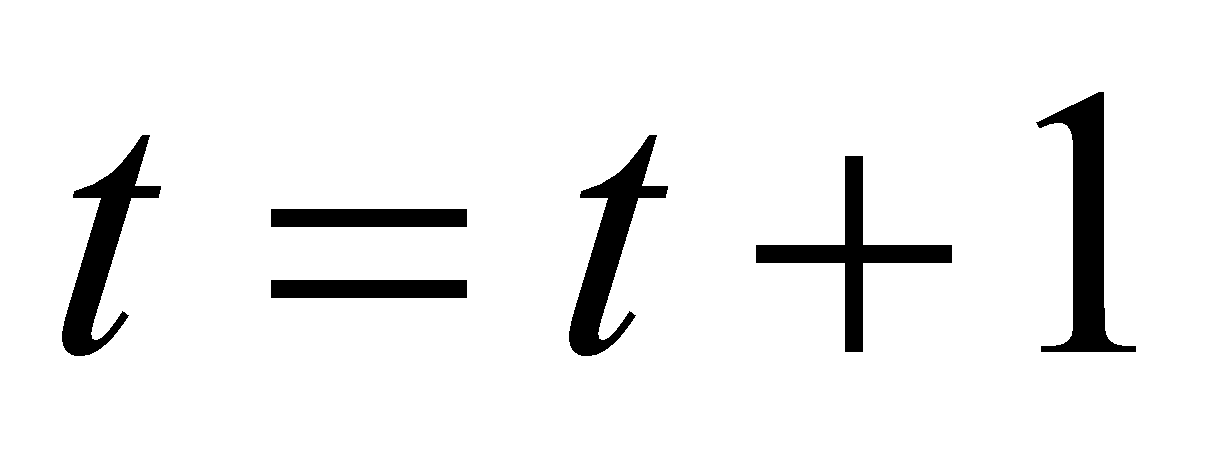ерации . Каждому интервалу ставится в соответствие некоторое значение функции плотности, в данном случае, значение функции плотности в середине подынтервала на предыдущей итерации . Производиться пересчет границ:

   1. Пересчет границ в соответствии с плотностью распределения: , здесь 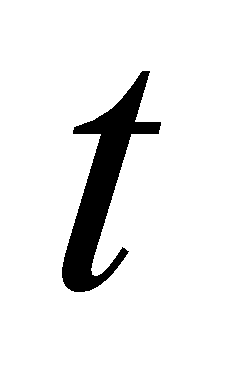- номер итерации, 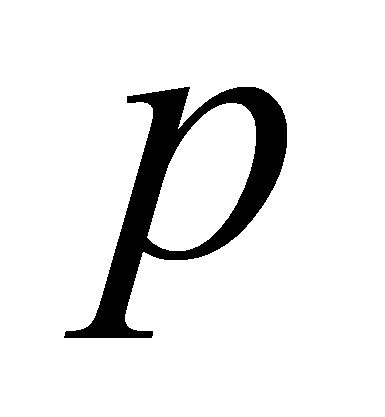- параметр, который отвечает за степень равномерности сетки границ;

   2. Масштабирование границ. Этот шаг необходим, для того чтобы вновь полученные границы соответствовали области . Масштабирование границ производится по формуле: ;

4. Проверяется условие остановки. Если изменение границ незначительно, то есть удовлетворяет критерий остановки 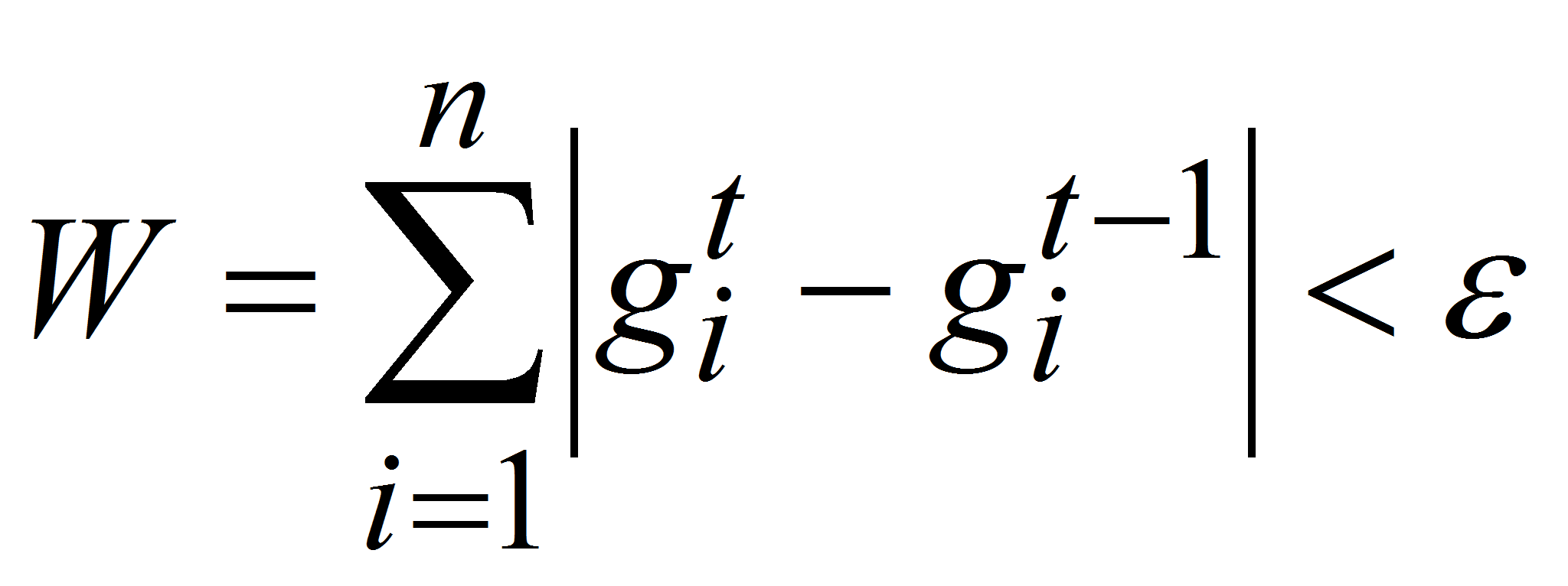, производится переход к шагу 4, иначе переход на шаг 2;

5. Генерация выборки. В каждой подынтервал генерируется случайное число, распределенное по равномерному закону.

Параметр используемый на шаге 3.1 влияет на степень равномерности сетки границ подынтервалов, чем больше значение параметра тем больше степень неравномерности сетки.

Исследования результатов работы алгоритма с неравномерной сеткой границ подынтервалов показывают возможность использования такого алгоритма для генерации выборок случайных величин с быстроизменяющейся функцией плотности распределения и большой дисперсией. Степень согласия получаемых выборок и закона распределения С.В. удовлетворительная, даже при небольших объемах выборки. Однако в ходе исследования была выявлена сложность с решением задачи настройки оптимального параметра равномерности сетки. Исследования показывают, что зависимость используемого критерия согласованности от параметра равномерности сетки имеет немонотонный и скачкообразный характер. Этот факт усложняет задачу оптимизации параметра равномерности сетки, для её решения становится необходимым использование автоматических методов оптимизации.

Заключение

В заключении можно отметить следующие пункты о прецизионном генераторе псевдослучайных чисел, рассмотренном в работе:

• Использование прецизионного генератора псевдослучайных чисел позволяет получить выборки независимых друг от друга значений случайных величин заданного объема с высокой степенью согласованности с законом распределения этих случайных величин;

• Алгоритм прецизионного генератора не зависит от закона распределения случайных величин и может быть использован для генерации выборок случайных величин распределенных по различным статистическим законам.

Литература:

1. Колмогоров А. Н. Основные понятия теории вероятностей. 2-е издание. М.: Наука, 1974.

2. Первушин В. Ф. Исследование П-генератора случайных чисел, распределенных по логнормальному закону. Секция «математические методы моделирования, управления и анализа данных». XV Международная научная конференция "Решетнёвские чтения". Красноярск. 2011г.

3. Первушин В. Ф., Сергеева Н. А. Генератор случайных чисел, распределенных по логнормальному закону. Секция «математические методы моделирования, управления и оптимизации». XIII Международная научная конференция, посвященная памяти генерального конструктора ракетно-космических систем академика М.Ф. Решетнева. Красноярск, 2009 г. СС. 448-449.