В данной работе описываются способы определения коэффициентов активности изотермической системы бензол — диметилсульфоксид с помощью эмпирических уравнений и с помощью модели UNIFAC.
Ключевые слова: коэффициенты активности, эмпирические модели, бинарная система, бензол, диметилсульфоксид.
Экспериментальные данные о составах равновесных фаз и общем давлении для системы бензол (1) — диметилсульфоксид (2) при температуре 40°С приведены в таблице 1.
Таблица 1
Составы равновесных фаз для системы бензол (1) –диметилсульфоксид (2) при общем давлении P температуре 40°С
|
X1, % мол. |
У1, %мол. |
Р, мм рт ст |
|
0 |
0 |
1,656 |
|
10 |
96,94 |
48,8 |
|
20 |
98,33 |
80,3 |
|
30 |
98,76 |
103 |
|
40 |
99 |
119,1 |
|
50 |
99,17 |
132,15 |
|
60 |
99,3 |
143,4 |
|
70 |
99,41 |
151,9 |
|
80 |
99,52 |
160,7 |
|
90 |
99,67 |
169,8 |
|
100 |
100 |
181,1 |
В связи с невысоким общим давлением в системе при заданной температуре и отсутствием сильной ассоциации компонентов в паровой фазе считаем последнюю идеальной, подчиняющейся закону Дальтона. При этом допущении расчет коэффициентов активности компонентов возможен по уравнению:
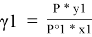
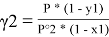
где х1, у1 — мольные доли бензола в жидкой и паровой фазе.
При x 1 = 0 общее давление соответствует давлению насыщенного пара второго компонента, а при x 1 = 100 % мол. — давлению насыщенного пара первого компонента. Таким образом, при 40°С Р° 2 = 1,656 мм рт. Ст., а Р° 2 = 181,1 мм рт. ст.
Результаты расчетов значений γ i и связанных с ними величин, которые необходимы для выполнения первой части задания — проверки термодинамической согласованности равновесных данных методом Редлиха — Кистера, приведены в табл. 2.
Таблица 2
Коэффициенты активности компонентов, рассчитанные по экспериментальным данным
|
x1, мол.д. |
γ1 |
γ2 |
ln(γ1) |
ln(γ2) |
ln(γ1/γ2) |
|
0,1 |
2,612187742 |
1,001932367 |
0,960188 |
0,001930503 |
0,958258 |
|
0,2 |
2,179983158 |
1,012235809 |
0,779317 |
0,012161557 |
0,767156 |
|
0,3 |
1,872313639 |
1,101794341 |
0,627175 |
0,09694007 |
0,530235 |
|
0,4 |
1,627678078 |
1,198671498 |
0,487155 |
0,181213858 |
0,305941 |
|
0,5 |
1,447301546 |
1,324692029 |
0,369701 |
0,281180001 |
0,088521 |
|
0,6 |
1,310474876 |
1,515398551 |
0,27039 |
0,415678474 |
-0,14529 |
|
0,7 |
1,191163446 |
1,803965378 |
0,174931 |
0,58998723 |
-0,41506 |
|
0,8 |
1,103869685 |
2,328985507 |
0,098822 |
0,845432768 |
-0,74661 |
|
0,9 |
1,038343825 |
3,383695652 |
0,037627 |
1,2189685 |
-1,18134 |
Таблица 3
Коэффициенты активности компонентов, рассчитанные по экспериментальным данным для составления зависимости коэффициентов активности компонентов системы бензол(1) — диметилсульфоксид (2) от состава
|
x1, мол.д. |
ln(γ1) |
ln(γ2) |
ln(γ1/γ2) |
|
0 |
1,1159 |
0 |
1,1159 |
|
0,1 |
0,960188085 |
0,001930503 |
0,958258 |
|
0,2 |
0,779317151 |
0,012161557 |
0,767156 |
|
0,3 |
0,627174906 |
0,09694007 |
0,530235 |
|
0,4 |
0,487154507 |
0,181213858 |
0,305941 |
|
0,5 |
0,36970082 |
0,281180001 |
0,088521 |
|
0,6 |
0,270389572 |
0,415678474 |
-0,14529 |
|
0,7 |
0,174930515 |
0,58998723 |
-0,41506 |
|
0,8 |
0,098821902 |
0,845432768 |
-0,74661 |
|
0,9 |
0,037626968 |
1,2189685 |
-1,18134 |
|
1 |
-0,0067 |
1,7853 |
-1,792 |
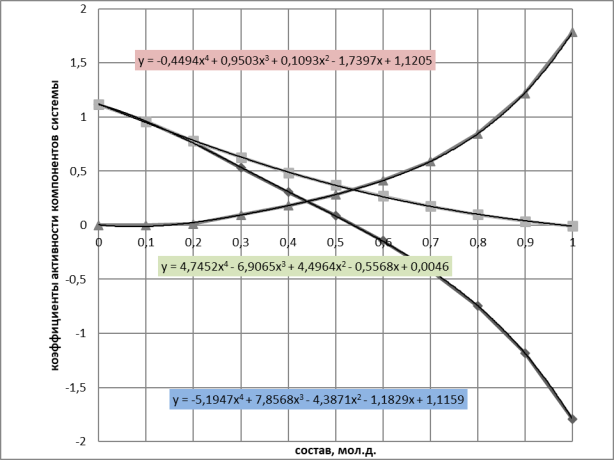
Рис. 1. Зависимость коэф.активности компонентов системы бензол(1) — диметилсульфоксил(2) и ln(γ1/γ2) от состава системы
В соответствии с методом Редлиха — Кистера условие термодинамической согласованности равновесных данных выражается уравнением:
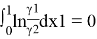
Площадь под интегральной кривой в положительной области S 1 = 0,3192, а в отрицательной области S 2 = 0,3318.
Площади S 1 и S 2 различаются на 0.0126 (<0,02), что свидетельствует о корректности полученных экспериментальных данных о равновесии жидкость — пар.
Эмпирические модели
Эмпирические модели непригодны для корреляции и предсказания данных, они служат лишь для математического описания массива экспериментальных данных о коэффициентах активности компонентов.
Одна из наиболее широко применяемых эмпирических моделей была предложена Редлихом и Кистером в 1948 г. В ней используется следующее разложение в ряд:
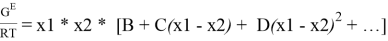
где x 1 , x 2 — мольные доли компонентов в растворе.
Из него получаются следующие трехпараметрические уравнения для коэффициентов активности компонентов бинарной системы:
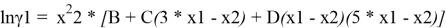
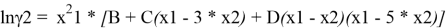
Вычитая из уравнения (3) уравнение (4) и учитывая, что для бинарной системы x1 + x2 = 1, получаем:
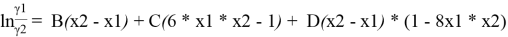
С использованием массива экспериментальных данных γ i (x i ) и уравнения (5), находят параметры B, C и D. Так, при x 1 = x 2 = 0.5 первое и третье слагаемое в правой части уравнения (5) обращается в 0 и рассчитывается значение C.
Из табл. 2 значение ln(γ1/γ2) = 0,0885, тогда константа С рассчитывается:
0.0885 = С(6*0.5*0.5–1); C= 0.177
При х 1 =0,1464 третье слагаемое в правой части уравнения (5) обращается в 0; ln(γ1/γ2) = 0,870, тогда константа В рассчитывается:
0,870 = В(0,8536–0,1464) + 0,188*(6*0,1464*0,8536–1); В= 1,312
При х 1 = 0,2113 ln(γ1/γ2) = 0,740 и из уравнения (5) рассчитывается константа D:
0,740 = 1,312*(0,7887–0,2113) + D*(0,7887–0,2113)*(1–8*0,2113*0,7887); D=0,0912
С использованием найденных констант В, С, D по уравнениям (3) и (4) рассчитывают значения lnγ 1 и lnγ 2 (табл. 4).
Таблица 4
Значения lnγ i , рассчитанные по эмпирическому уравнению Редлиха — Кистера
|
x1, мол.д. |
ln(γ1) |
ln(γ2) |
|
0,1 |
1,000337 |
0,011728 |
|
0,2 |
0,81002 |
0,04544 |
|
0,3 |
0,645926 |
0,100569 |
|
0,4 |
0,501359 |
0,178735 |
|
0,5 |
0,37225 |
0,28375 |
|
0,6 |
0,257156 |
0,421612 |
|
0,7 |
0,15726 |
0,600509 |
|
0,8 |
0,076373 |
0,830817 |
|
0,9 |
0,020932 |
1,125103 |
Для расчета констант уравнения Маргулеса с использованием линейного уравнения G E /( RT * x 1 * x 2 ) = А+(В-А)х 1 н аходят значения избыточной энергии Гиббса по уравнению:
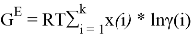
Например, при х 1 = 0,1:
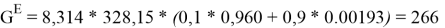
Таблица 5
Значения избыточной энергии Гиббса и функции G E /( RT * x 1 * x 2 )
|
x1, мол.д. |
G Е |
функция |
|
0,1 |
266,702453 |
1,086181 |
|
0,2 |
451,7764124 |
1,034954 |
|
0,3 |
698,4579127 |
1,219098 |
|
0,4 |
828,26643 |
1,264959 |
|
0,5 |
887,8792532 |
1,301762 |
|
0,6 |
896,2405482 |
1,368771 |
|
0,7 |
816,9644581 |
1,425941 |
|
0,8 |
676,9963688 |
1,5509 |
|
0,9 |
424,9535803 |
1,730679 |
Зависимость функции G E /(RT*x 1 *x 2 ) от х 2 представлена на рисунке 2.
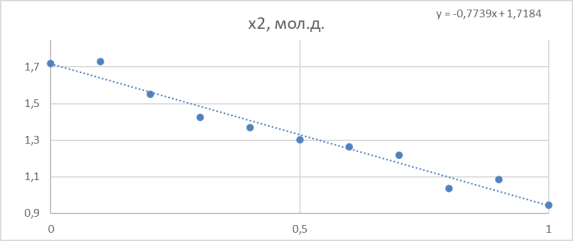
Рис. 2. Линейная зависимость G E /(RT*x 1 *x 2 ) = B + (A-B)*x 2 для расчета констант уравнения Маргулеса
По отрезку, отсекаемому прямой на оси ординат, находят параметр B (т. к. зависимость от x 2 , а по значению тангенса угла наклона прямой рассчитывают второй параметр (параметр А) в уравнениях Маргулеса.
Судя по графику на рисунке 2, некоторые точки из табл. 5 отклоняются от прямой. С учетом остальных точек строится прямая, отсекающая на оси ординат в соответствии с уравнением G E /( RT * x 1 * x 2 ) = B + ( A - B )* x 2 отрезок, соответствующий константе В = 1,72.
Тангенс угла наклона прямой tgα= -0,664; tgα = A — B, следовательно,
A = 1,72–0,664 = 1,056. Далее с использованием уравнений Маргулеса:
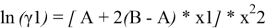
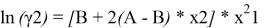
рассчитывают значения lnγ1 и lnγ2
Таблица 6
Значения lnγ i , рассчитанные по эмпирическому уравнению Маргулеса
|
x1, мол.д. |
ln(γ1) |
ln(γ2) |
|
0,1 |
0,962928 |
0,005248 |
|
0,2 |
0,845824 |
0,026304 |
|
0,3 |
0,712656 |
0,071136 |
|
0,4 |
0,571392 |
0,147712 |
|
0,5 |
0,43 |
0,264 |
|
0,6 |
0,296448 |
0,427968 |
|
0,7 |
0,178704 |
0,647584 |
|
0,8 |
0,084736 |
0,930816 |
|
0,9 |
0,022512 |
1,285632 |
Для определения констант уравнения ван Лаара рассчитывают значения
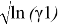
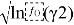
Таблица 7
Значения
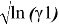
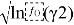
|
x 1 , мол.д. |
|
|
|
0 |
0,9984 |
0 |
|
0,1 |
0,979892 |
0,043937 |
|
0,2 |
0,882789 |
0,110279 |
|
0,3 |
0,791944 |
0,311352 |
|
0,4 |
0,697965 |
0,425692 |
|
0,5 |
0,60803 |
0,530264 |
|
0,6 |
0,51999 |
0,644731 |
|
0,7 |
0,418248 |
0,768106 |
|
0,8 |
0,31436 |
0,919474 |
|
0,9 |
0,193977 |
1,104069 |
|
1 |
0 |
1,355417 |
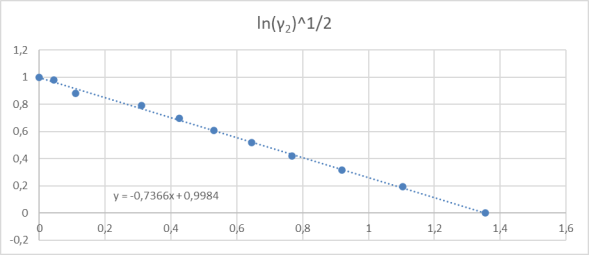
Рис. 3. Линейная зависимость для определения констант уравнения ванн Лаара
Отрезок, отсекаемый прямой на оси ординат, соответствует
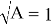
Тангенс угла наклона прямой tgα =
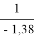
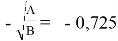
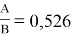
С использованием уравнения ван Лаара рассчитывают значения ln(γ1) и ln(γ2).
Уравнения ван Лаара:
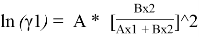
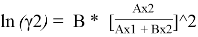
Таблица 8
Значения lnγ i , рассчитанные по эмпирическому уравнению ван Лаара
|
x1, мол.д. |
ln(γ1) |
ln(γ2) |
|
0,1 |
0,892607055 |
0,005796865 |
|
0,2 |
0,78105823 |
0,02567919 |
|
0,3 |
0,66590484 |
0,064339323 |
|
0,4 |
0,54813426 |
0,128151092 |
|
0,5 |
0,42940666 |
0,225884619 |
|
0,6 |
0,312428735 |
0,369786772 |
|
0,7 |
0,201555265 |
0,577252205 |
|
0,8 |
0,103779842 |
0,873475786 |
|
0,9 |
0,03041106 |
1,2957895 |
Теоретические модели. Метод UNIFAC (UNIquac Functional — group Activity Coefficients).
Молекула бензола представляется в виде 6 групп АСН, а молекула диметилсульфоксида — как одна группа Me 2 SO. Параметры объема R k и поверхности групп Q k приведены в таблице 9.
Параметры взаимодействия групп: а 12 = 169,9; а 21 = -2,504.
Приведенные параметры группового взаимодействия, рассчитанные по уравнению:
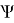
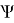
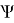
Таблица 8
Параметры объема и поверхности групп АСН и Me 2 SO
|
N группы |
Группа |
R k |
Q k |
Количество групп в молекуле |
|
|
Бензол |
Диметилсульфоксид |
||||
|
1 |
АСН |
0.5313 |
0.400 |
6 |
0 |
|
2 |
Ме 2 SO |
2.8266 |
2.472 |
0 |
1 |
Ван-дер-ваальсовы радиусы молекул компонентов:
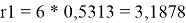
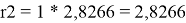
Ван-дер-ваальсовы поверхности молекул компонентов:
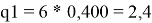
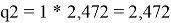
Объемная доля компонентов в растворе, рассчитанная по уравнению:
ϕ
i
=
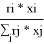
ϕ
1
=
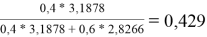
Доля площади поверхности молекул компонентов в растворе, рассчитанная по уравнению:
ϴ
i
=
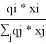
ϴ
1
=
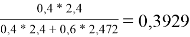
Факторы объемности молекул компонентов, рассчитанные по уравнению:
l i = Z/2* (r i -q i )-(r i -1),(14)
где Z=10 — координационное число.
l 1 = 10/2*(3,1878–2,4) — (3,1878–1) = 1,7512
l 2 = 10/2*(2,8266 - 2,472) — (2,8266–1) = -0,0536
Далее используют уравнения:
lnγ 1(комб) = ln
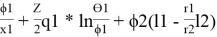
lnγ
2(комб)
= ln
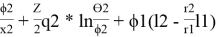
lnγ
1(комб)
=ln
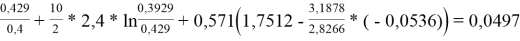
lnγ
2(комб)
= ln
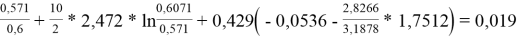
Групповые доли групп в растворе при х 1 =0,4, рассчитанные по уравнению:
x̅
j
=
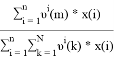
x̅ 1 =
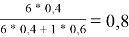
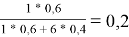
Доля площади поверхности групп в растворе рассчитывается по уравнению:
ϴ
m
= (x̅
m
* Q
m
)/(
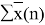
ϴ
1
=
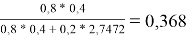
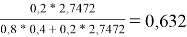
Молекула бензола состоит только из групп АСН, поэтому для чистого бензола ϴ 1 = 1; аналогично для чистого диметилсульфоксида ϴ 2 = 1
Таблица 10
Доля площади поверхности групп в растворе и в чистых компонентах
|
Параметр |
Раствор |
Бензол |
Диметилсульфоксид |
|
ϴ 1 |
0,368 |
1 |
- |
|
ϴ 2 |
0,632 |
- |
1 |
Средневзвешенные параметры взаимодействия групп рассчитывают по уравнению:
Е
k
= ϴ
1
*
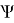
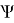
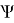
E 1 = 0,368*1 + 0,632*1,00803 = 1,0051
E 2 = 0,368*0,58126 + 0,632*1 = 0,8459
Таблица 11
Средневзвешенные параметры взаимодействия групп в растворе и для чистых компонентов
|
Параметр |
Раствор |
Бензол |
Диметилсульфоксид |
|
Е 1 |
1,0051 |
1 |
- |
|
Е 2 |
0,8459 |
- |
1 |
Значения дополнительной функции F i рассчитывают по уравнению (20) и приводят для раствора и чистых компонентов в табл. 12:
F k =
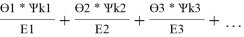
F
1
=
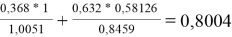
F
2
=
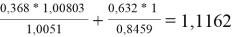
Таблица 12
Дополнительные функции групп в растворе и для чистых компонентов
|
Параметр |
Раствор |
Бензол |
Диметилсульфоксид |
|
F 1 |
0,8004 |
1 |
- |
|
F 2 |
1,1162 |
- |
1 |
Коэффициенты активности групп в растворе рассчитываются по уравнению (21) и в чистых компонентах — по уравнению (22):
lnГ k = Q k (1-lnE k — F k ) (21)
lnГ i k = Q i k (1-lnE i k — F i k ) (22)
lnГ 1 = 0,4*(1 — ln1,0051–0,8004) = 0,07781;
lnГ 2 = 2,472*(1 — ln0,8459–1,1162) = 0,12645;
lnГ 1 1 = 0,4*(1 — ln1–1) = 0;
lnГ 2 2 = 2,472*(1 — ln1–1) = 0.
Далее рассчитывают коэффициенты активности компонентов с учетом комбинаторной и остаточной составляющих по уравнениям (23) и (24):
lnγ i = lnγ i (комб) + lnγ i (ост) (23)
lnγ
i
(ост)
=
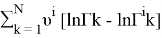
lnγ 1 = 0,0497 + 6*(0,07781–0) = 0,51656
lnγ 2 = 0,019 + 1*(0,12645–0) = 0,14545
γ 1 = 1,676; γ 2 = 1,157
Погрешности расчета γ 1 и γ 2 при х 1 = 0,4 мол.д.
При γ 1 = 1,676 и γ 2 = 1,157 по методу UNIFAC:
Δ
1
=
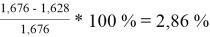
Δ
2
=
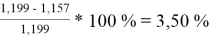
При γ 1 = 1,651 и γ 2 = 1,196 по методу Редлиха — Кистера:
Δ
1
=
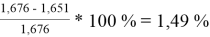
Δ
2
=
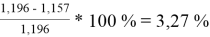
При γ 1 = 1,771 и γ 2 = 1,159 по методу Маргулеса:
Δ
1
=
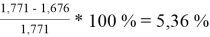
Δ
2
=
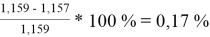
При γ 1 = 1,730 и γ 2 = 1,137 по методу ван Лаара:
Δ
1
=
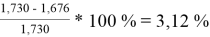
Δ
2
=
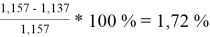
Коэффициенты активности компонентов при x 1 = 40 % мол. методом UNIFAC: при γ 1 = 1,676 с погрешностью расчета Δ 1 = 2,86 % и при γ 2 = 1,157 с погрешностью расчета Δ 2 = 3,50 %.
Литература:
- Гайле, А. А. Процессы разделения и очистки продуктов переработки нефти и газа / А. А. Гайле, В. Е. Сомов, А. В. Камешков. — 2. — 2018: Химиздат, 2018. — 432 c.
- Адлард, Э. Газовая хроматография / Э. Адлард, М. Кан., Б. Уитхем // Журн. приклад. химии. — 1964. — № 4. — С. 334–344.