В статье рассматриваются коррекция искажений сигнала на выходе цифрового фильтра при пропусках отсчетов сигнала на входе.
Ключевые слова: гармоническая функция, сигнал с пропусками, цифровой фильтр.
При обработке результатов некоторых физических экспериментов используется модель данных в виде полигармонических функций, например, в таком виде рассматриваются данные астрономических наблюдений [1], данные съема значений напряженности электрического поля Земли [2] и др.
Естественным является наличие пропусков в данных наблюдений, которые вызваны периодическими особенностями эксперимента либо отказами в работе аппаратуры. Полученные последовательности носят название неравномерных временных рядов. Анализ подобных рядов в спектральной области, зависимость результатов обработки от характеристик пропусков и параметров методов спектрального анализа приведена в [3].
В работе рассматривается анализ неравномерных временных рядов во временной области при фильтрации сигнала узкополосным фильтров для выделения одной составляющей полигармонического сигнала.
Пусть временной ряд представляет собой полигармоническую функцию
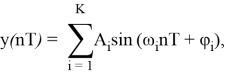
где A i , ω i и φ i — амплитуда, частота и начальная фаза i -й гармонической составляющей сигнала.
Рассмотрим временной ряд z(nT) , образованный пропусками отсчетов сигнала y(nT) с N 1 по N 2 отсчеты
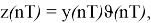
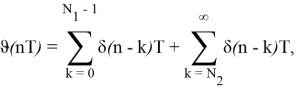
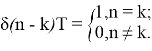
Найдем отклик y(nT) и z(nT) на выходе узкополосного нерекурсивного фильтра с импульсной характеристикой h M (nT) , настроенного на частоту М -й составляющей сигнала. Импульсная характеристика имеет вид
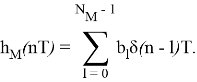
Для исходного ряда выходной сигнал фильтра — свертка сигнала и импульсной характеристики (операция *)
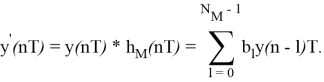
Так как фильтр выделяет только сигнал с частотой ω M , сигнал y’(nT) можно представить в виде
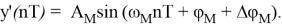
Для сигнала с пропусками -
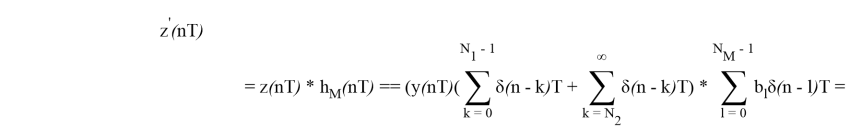
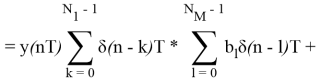
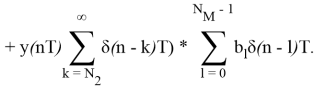
Представим входной сигнал с пропусками в виде
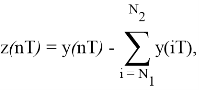
Тогда, учитывая дистрибутивность свертки, можно записать
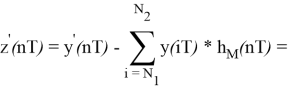
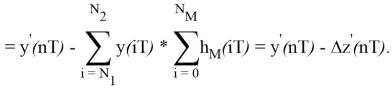
Свертка двух последовательностей разной длины — последовательность, длина которой равна сумме длин последовательностей минус 1, т. е.
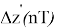
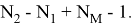
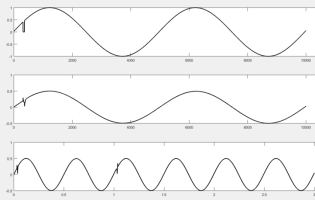
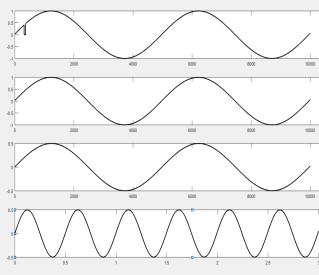
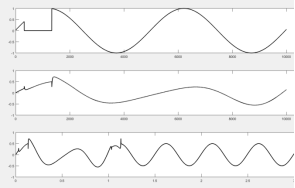
Моделирование пропуска данных для гармонического сигнала подтвердило, что наличие пропуска отсчетов влияет на выходной сигнал фильтра на интервале импульсной характеристики фильтра плюс длительность пропуска (рисунки 1а, 2а и 3а). На первом графике рисунков — сигнал с пропуском, на втором — сигнал на выходе фильтра в одном масштабе с первым графиком, на третьем графике — выход на временном интервале, превышающем длительность импульсной характеристики фильтра.
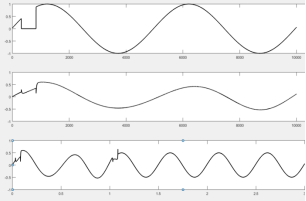
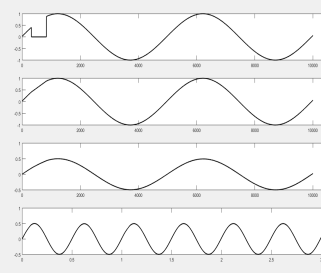
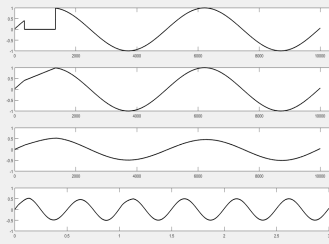
При замене пропусков входного сигнала линейной функцией, искажения на выходе фильтра уменьшаются. Это проиллюстрировано на рисунках 1б, 2б и 3б.
|
|
|
|
а) |
б) |
Рис. 1. Количество пропущенных отсчетов — 51 (1 % периода сигнала)
|
|
|
|
а) |
б) |
Рис. 2. Количество пропущенных отсчетов — 518 (10 % периода сигнала)
Анализ сигнала заданной частоты в составе полигармонического сигнала можно выполнить по следующему алгоритму:
1) Расчет узкополосного фильтра;
1-я итерация (шаги 2–4):
2) расчет отклика фильтра на исходный сигнал;
|
|
|
|
а) |
б) |
Рис. 3. Количество пропущенных отсчетов — 1018 (20 % периода сигнала)
3) определение оценки амплитуды отклика и коэффициента передачи фильтра на частоте исследуемого сигнала;
4) коррекция исходного сигнала на интервале пропуска — замена нулевых отсчетов линейной функцией;
Выполнение следующей итерации. Анализ завершается, когда сигналы, полученные на двух соседних итерациях, отличаются не более чем на 10 % или при достижении максимального числа итераций.
Литература:
- Теребиж, В. Ю. Анализ временных рядов в астрофизике / В. Ю. Теребиж. — М.: Наука, 1992. — 394 c. — Текст: непосредственный.
- Ефимов, В. А. Структура вариаций электрического поля земли в диапазоне частот 10–5...2,5∙10–5 ГЦ / В. А. Ефимов, Л. А. Калыгина. — Текст: непосредственный // Динамика сложных систем — XXI век. — 2015. — № 2. — С. 29–37.
- Витязев, В. В. Анализ неравномерных временных рядов: Учеб. пособ. / В. В. Витязев. — СПб.: Изд-во С.-Петерб. ун-та, 2001. — 68 c. — Текст: непосредственный.